Thompson Sampling이란?
주어진 개의 액션에 해당하는 reward의 추정치 가 확률 분포를 따른다고 가정하는 것이다.
이때 많이 사용하는 확률 분포는 베타 분포이다.
MAB와의 가장 큰 차이점은 각각의 액션의 reward 추정치를 확률이 아닌 확률 분포를 사용하는 것이다.
베타 분포(Beta Distribution)
두 개의 양의 변수 , 로 표현할 수 있는 확률 분포이며, 0과 1 사이의 값을 갖는다.
여기서 는 , 에 의해 정해지는 베타 함수이다.
Thompson Sampling 예시
사용자에게 보여줄 수 있는 광고 배너가 있다고 가정한다.
세 개의 배너 중 어떤 배너를 노출했을 때 가장 높은 클릭을 유도할 수 있는지를 구하고자 한다.
베타 분포에 필요한 데이터는 두 가지인데, 베너를 보고 클릭한 횟수()와 배너를 보고 클릭하지 않은 횟수()이다.
현재까지 얻어진 데이터는 다음과 같다고 가정한다.
| 배너 |
click() |
non-click() |
표본 평균 |
| banner1 |
3 |
10 |
|
| banner2 |
2 |
4 |
|
| banner3 |
1 |
9 |
|
Greedy algorithm으로 구하면 표본 평균이 가장 큰 banner2를 선택하여 노출할 것이다.
그러나 Thompson Sampling에서는 배너를 클릭할 확률이 을 따른다고 보는 것이다.
데이터가 없는 상태
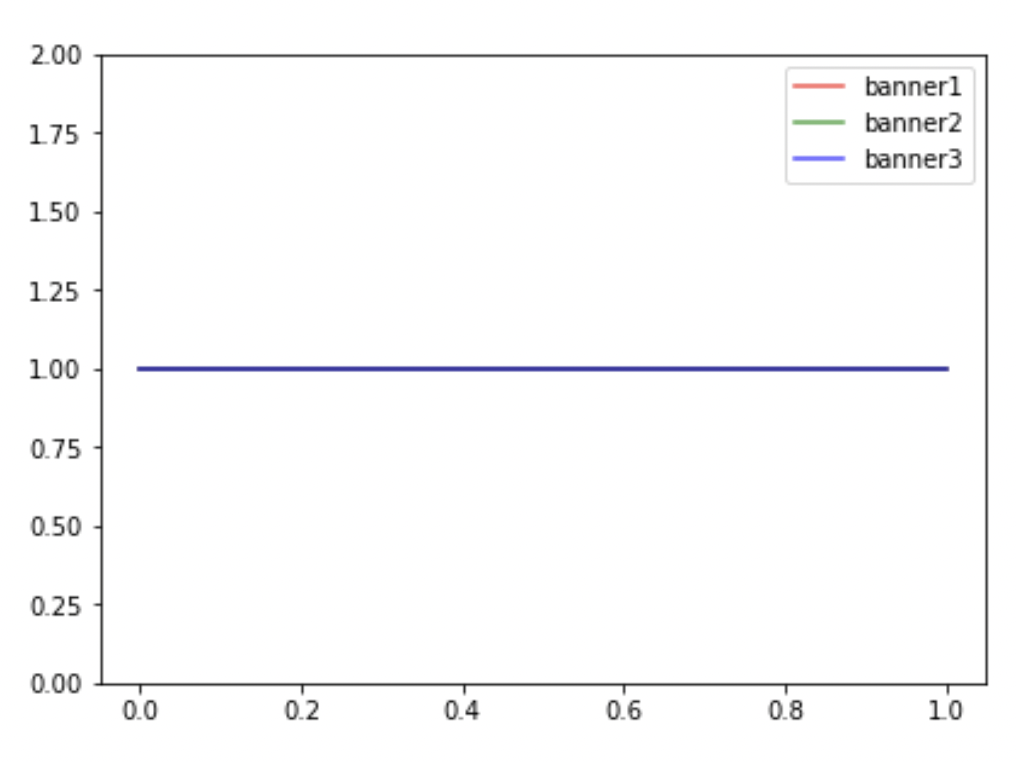
- banner1 ~ Beta(1, 1)
- banner2 ~ Beta(1, 1)
- banner3 ~ Beta(1, 1)
랜덤하게 노출
Step 1
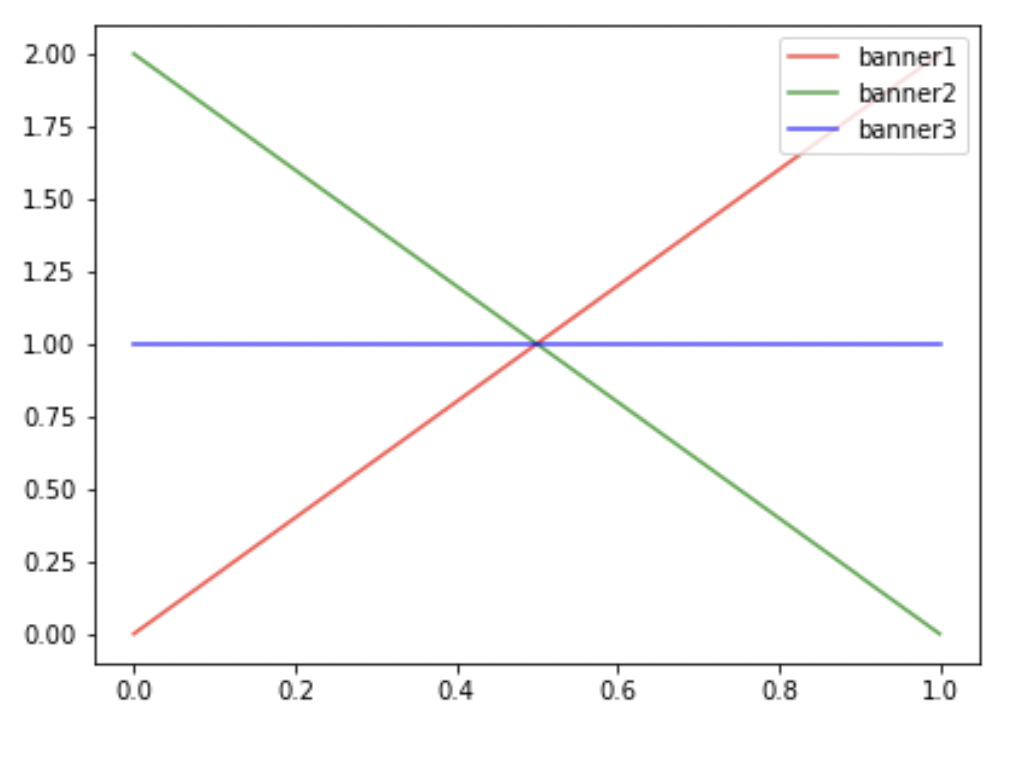
- banner1 ~ Beta(2, 1)
- banner2 ~ Beta(1, 2)
- banner3 ~ Beta(1, 1)
Step 2
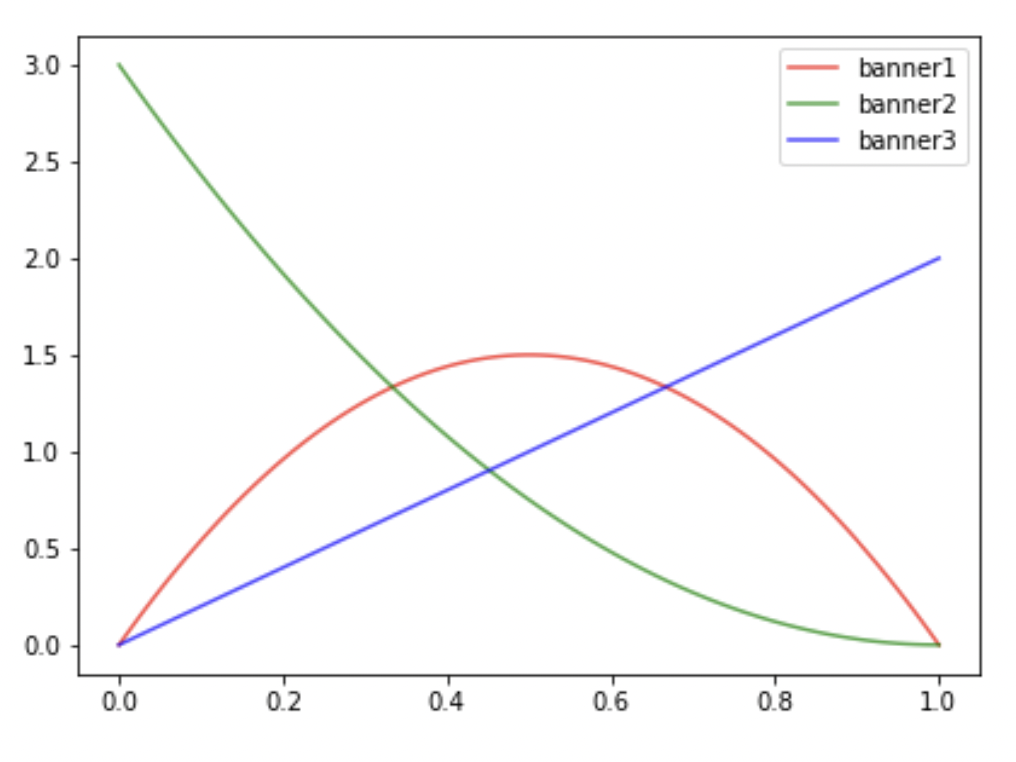
- banner1 ~ Beta(2, 2)
- banner2 ~ Beta(1, 3)
- banner3 ~ Beta(2, 1)
Step 3
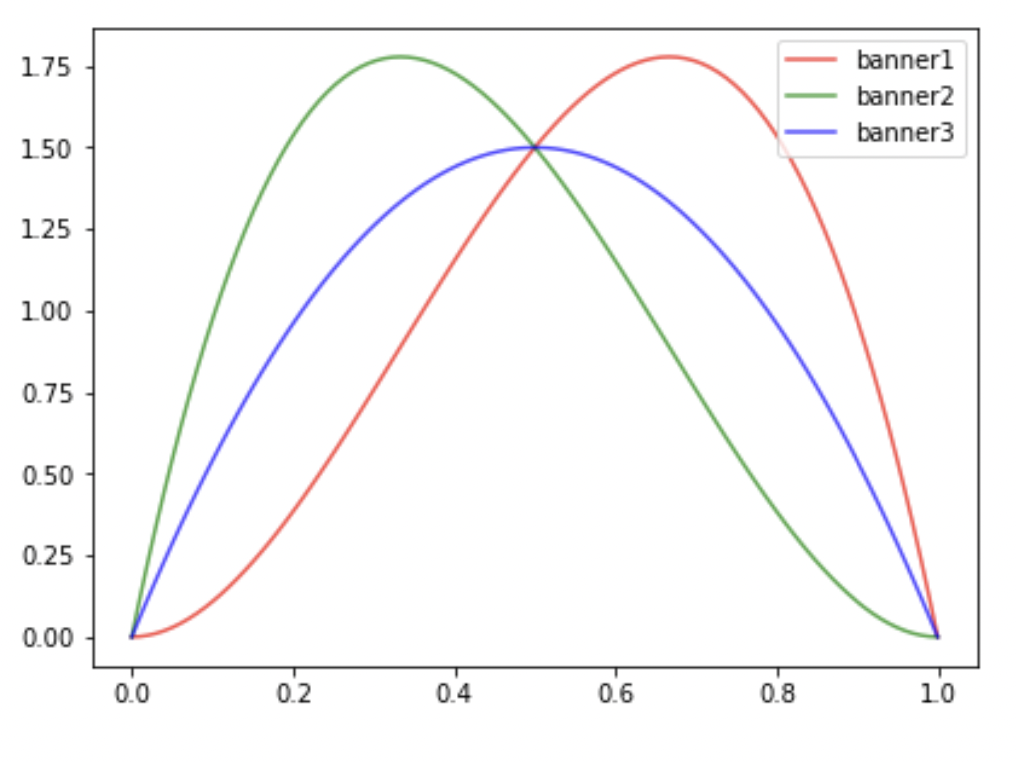
- banner1 ~ Beta(3, 2)
- banner2 ~ Beta(2, 3)
- banner3 ~ Beta(2, 2)
베타 분포에서 샘플링하여 노출
현재까지의 베타 분포
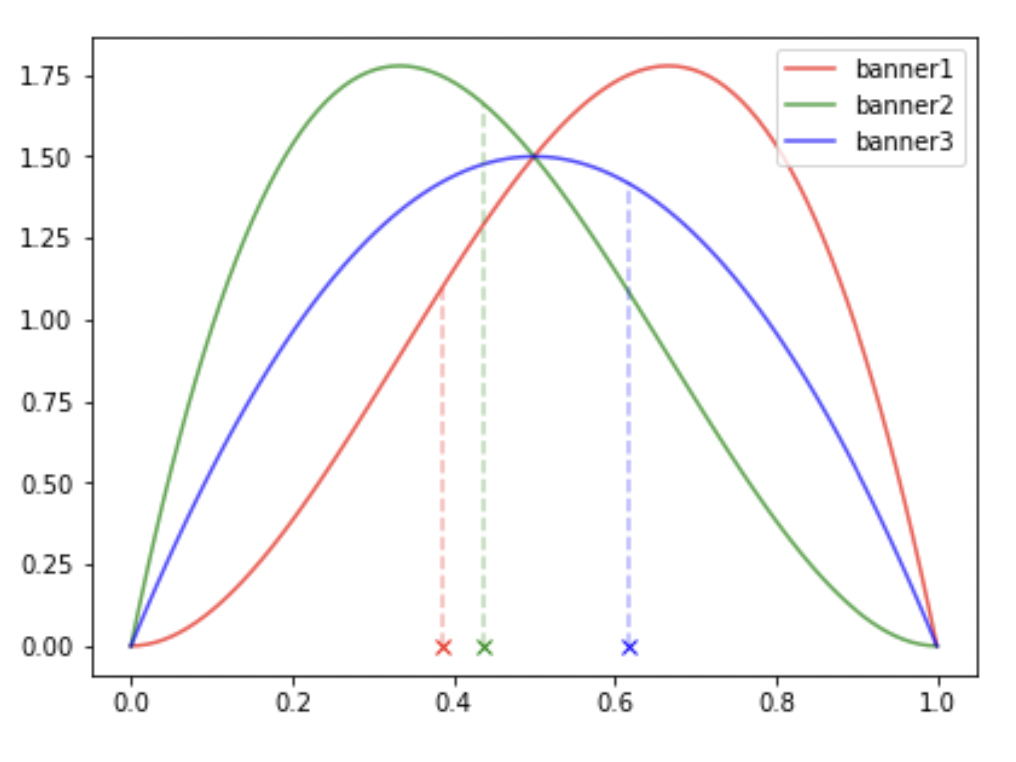
- banner1 ~ Beta(3, 2)
- banner2 ~ Beta(2, 3)
- banner3 ~ Beta(2, 2)
샘플링 결과
- banner1: 0.386
- banner2: 0.438
- banner6: 0.616
⇒ 가장 확률이 높은 banner3를 노출시킨다. 노출시킨 banner3를 유저가 클릭했는지 안 했는지를 반영하여 다음 베타 분포를 반영한다.
이런 방법으로 베타 분포를 업데이트해 가면서 결과적으로 가장 reward가 크게끔 하는 가능도로 각 banner 별 확률분포가 수렴하게 된다.
확률(probability)과 가능도(likelihood)의 차이
확률은 어떠한 확률 분포 또는 파라미터가 주어졌을 때 특정 관측값이 나올 가능성 또는 범위 안에 속할 가능성을 구하는 것이다.
가능도는 어떠한 관측 값이 주어졌을 때, 해당 관측값이 어떠한 확률 분포 또는 파라미터에서 나왔을지에 관한 가능성이다.
즉, 특정 관측값이 나올 가능성이 높은 확률 분포 또는 파라미터를 구하기 위해 사용한다.
LinUCB(Linear UCB)
[참고 자료] https://yjjo.tistory.com/44
Contextual Bandits - LinUCB
금번 포스팅을 시작하면서 multi-armed bandit 포스팅의 초반부를 상기시켜보겠습니다. Bandit을 크게 stochastic, non-stochastic으로 분류했고, 그 다음 분류는 context-free, context로 분류했습니다. 지금까지..
yjjo.tistory.com
Contextual Bandit
Context
유저의 데모그래픽이나 아이템의 카테고리, 태그와 같은 여러 특성인 부가 정보를 의미한다.
Context-Free Bandit
동일한 액션에 대해 유저의 context 정보에 관계 없이 항상 동일한 reward를 가진다.
카지노의 슬롯머신의 경우에는 슬롯머신마다 reward 확률이 다를 수는 있지만 어떠한 사람이 사용하더라도 사람마다 확률이 달라지지 않는다.
Contextual Bandit의 정의
유저의 context 정보에 따라 동일한 액션이더라도 다른 reward를 가질 수 있도록 반영한다.
동일한 스포츠 기사를 보더라도 나이 및 성별에 따라 클릭 성향이 다를 수 있으므로 개인화 추천을 해야 하며, 이때 contextual bandit을 적용해볼 수 있다.
Context를 사전에 관측 가능한 정보로 생각하면 좀 더 이해하기가 편하다.
LinUCB with Disjoint Linear Models
Arm-Selection Strategy
: 시점에서의 액션 에 대한 -차원의 context 벡터
: 액션 에 대한 -차원의 학습 파라미터 (coefficient vector)
: 시점의 개의 context 벡터(학습 데이터)로 구성된 행렬
은 expected reward를 선형 함수로 나타낸 것이며, 주어진 context 상황에서 액션 를 선택할 때 얻는 reward를 의미한다.
즉, 로 표현할 수 있으며, context에서 액션 를 선택했을 때 reward의 기댓값을 나타낸다.
선형 변환 식으로 reward를 나타낼 수 있기 때문에 linear UCB라고 불린다.
를 액션 별로 따로 구성해서 학습하면 disjoint model, 이를 공유해서 학습하면 hybrid model이라고 구분한다.
여기서는 액션별로 따로 구성한 를 사용하므로 disjoint model이 된다.
는 액션에 대한 exploration을 추가해 주는 term이다.
Variance가 커지는 것을 막기 위해 패널티를 추가하는 것이며, ridge regression에 해당된다.
시간이 지나면서 학습 데이터를 많이 수집할수록 exploration term은 점점 작아지고, 최종적으로 expected reward로 수렴하게 된다.
LinUCB 예시
세 명의 유저와 세 개의 아이템이 존재하고, Context 벡터가 4차원으로 구성되어 있다고 가정한다.
Context Vector
- 첫 번째 차원: male
- 두 번째 차원: female
- 세 번째 차원: young
- 네 번째 차원: old
User의 Context Vector
Item과 Action
최종 학습 파라미터
- 첫 번째 액션에 관한 학습 파라미터
- 두 번째 액션에 관한 학습 파라미터
- 세 번째 액션에 관한 학습 파라미터
Naver AiRS 추천 시스템
인기도 기반 필터링을 통해 탐색 대상을 수 천개의 아이템으로 축소한 후, contextual bandit 알고리즘을 통해 유저의 취향을 탐색하고 활용한다.
https://tv.naver.com/v/16968202
뭐볼까? : 네이버 AiRS 인공지능 콘텐츠 추천의 진화
NAVER Engineering | 김창봉 / 김도희 / 이태영 - 뭐볼까? : 네이버 AiRS 인공지능 콘텐츠 추천의 진화
tv.naver.com
출처
1. 네이버 부스트캠프 AI Tech 추천시스템 Stage 2 기초 강의
2. https://yjjo.tistory.com/44