Memory-based와 Model-based Collaborative Filtering

 

 

Memory-based Collaborative Filtering

 

Memory-based CF는 다른 말로 Neighborhood-based CF(이웃 기반 CF)이라고도 하며, 사용자 또는 아이템 간의 similarity 값을 계산하고 이를 평점 예측 또는 Top-K ranking에 활용하는 방법이다.

Similarity 값을 계산하는 metric은 여러 종류가 있으며, Jaccard Similarity, Cosine Similarity, Pearson Similarity 등이 활용된다.

 

$$ \text{Jaccard}(i, j) = \frac{|U_i \cap U_j}{|U_i \cup U_j|} $$

 

Jaccard 유사도는 집합들 간의 포함 관계를 사용하는 metric이다.

 

$$ \text{Cosine}(u, v) = \frac{R_u \cdot R_v}{|R_u| \cdot |R_v|} $$

 

Cosine 유사도는 서로 다른 두 벡터 사이의 각거리를 계산하는 것이다.

 

$$ \text{Pearson}(u, v) = \frac{\sum_{i \in I_u \cap I_v} (R_{u_i} - \bar{R}_u) (R_{v, i} - \bar{R}_v)}{\sqrt{\sum_{i \in I_u \cap I_v}(R_{u_i} - \bar{R}_u)^2} \sqrt{\sum_{i \in I_u \cap I_v}(R_{v_i} - \bar{R}_v)^2}} $$

 

Pearson 유사도는 평균을 빼서 남은 잔차값에 대한 Cosine 유사도와 비슷하다.

 

Memory-based CF의 평점 예측은 '어떤 한 사용자가 이전에 평점을 매긴 다른 아이템의 가중치 합으로 원하는 아이템의 평점을 예측한다'는 간단한 huristic rule에 의해 이루어진다.

다시 말해, 사용자가 아이템에 부여할 평점은 다른 유사한 사용자가 부여한 또는 유사한 아이템에 부여된 평점을 기반으로 추정할 수 있으며 이때 유사한 사용자 또는 아이템일수록 더 높은 중요도를 가지게 된다.

 

아이템 간의 CF는 다음과 같이 아이템 $i$와 가장 유사한 아이템들인 $j$에 사용자 $u$가 부여한 평점인 $R_{u, j}$에 주목한다.

여기서 유사한 아이템이라는 건 사용자 $u$가 평가한 아이템 $i$ 이외의 다른 아이템을 의미한다.

 

$$ r(u, i) = \frac{\sum_{j \in I_u \setminus \{ i \}}R_{u, j} \cdot \text{Sim}(i, j)}{\sum_{j \in I_u \setminus \{ i \}} \text{Sim}(i, j)} $$

 

사용자 간의 CF는 다음과 같이 사용자 $u$와 가장 유사한 사용자들인 $v$가 아이템 $i$에 부여한 평점인 $R_{v, i}$에 주목한다.

여기서 유사한 사용자라는 건 아이템 $i$ 을 평가한 사용자 $u$ 이외의 다른 사용자를 의미한다.

 

$$ r(u, i) = \frac{\sum_{v \in U_{i} \setminus \{ u \}}R_{v, i} \cdot \text{Sim}(u, v)}{\sum_{v \in U_{i} \setminus \{ u \}} \text{Sim}(u, v)} $$

 

 

Amazon.com에서는 2003년에 Jaccard 유사도와 함께 이러한 아이템 간(Item-to-Item) CF를 기반으로 하는 추천 시스템 논문을 발표했다.

이때는 아이템 간 Cosine 유사도에 기반하여 연관 상품 추천 알고리즘을 구현했다.

어떠한 아이템이 주어졌을 때, Amazon.com이 그 아이템과 자주 같이 구매된 아이템들을 추천해준다는 아이디어를 기반으로 한다.

약 2,900만 명의 사용자, 수백만 개의 아이템을 대상으로 유사 아이템 테이블을 비교적 비싼 컴퓨팅 자원을 요구하는 offline에서 계산하고, online에서는 비교적 빠른 look-up operation을 수행한다.

현재도 대규모의 트래픽을 제어하는 서비스에서는 Memory-based CF가 간단하지만 효과적인 베이스라인이 될 수 있다.

 

 

 

 

Model-based Collaborative Filtering

 

Latent Factor Model

 

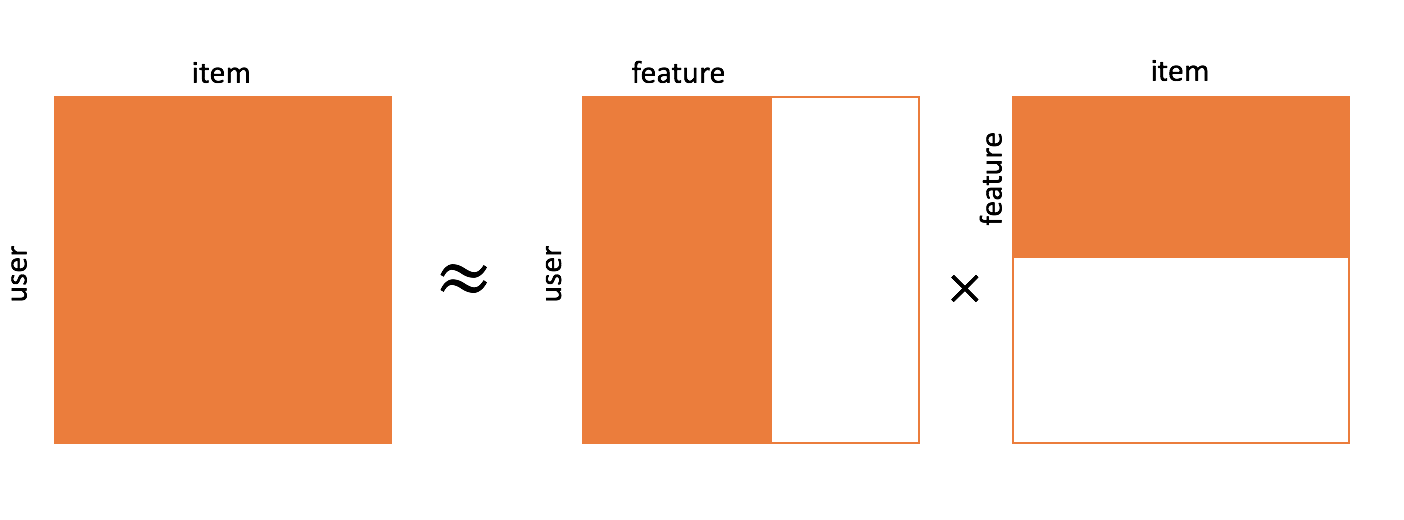
[출처] https://commons.wikimedia.org/wiki/File:Matrix_factorization.png, Xianteng

 

사용자와 아이템의 저차원 표현을 학습하는 것으로 볼 수 있다.

명시적인 feature를 사용하지 않고도 상호작용 행렬인 $R$로부터 잠재적인 의미를 갖는 $\gamma_U$, $\gamma_I^T$ 표현들을 학습하기 때문에 latent factor model이라고도 한다.

 

 

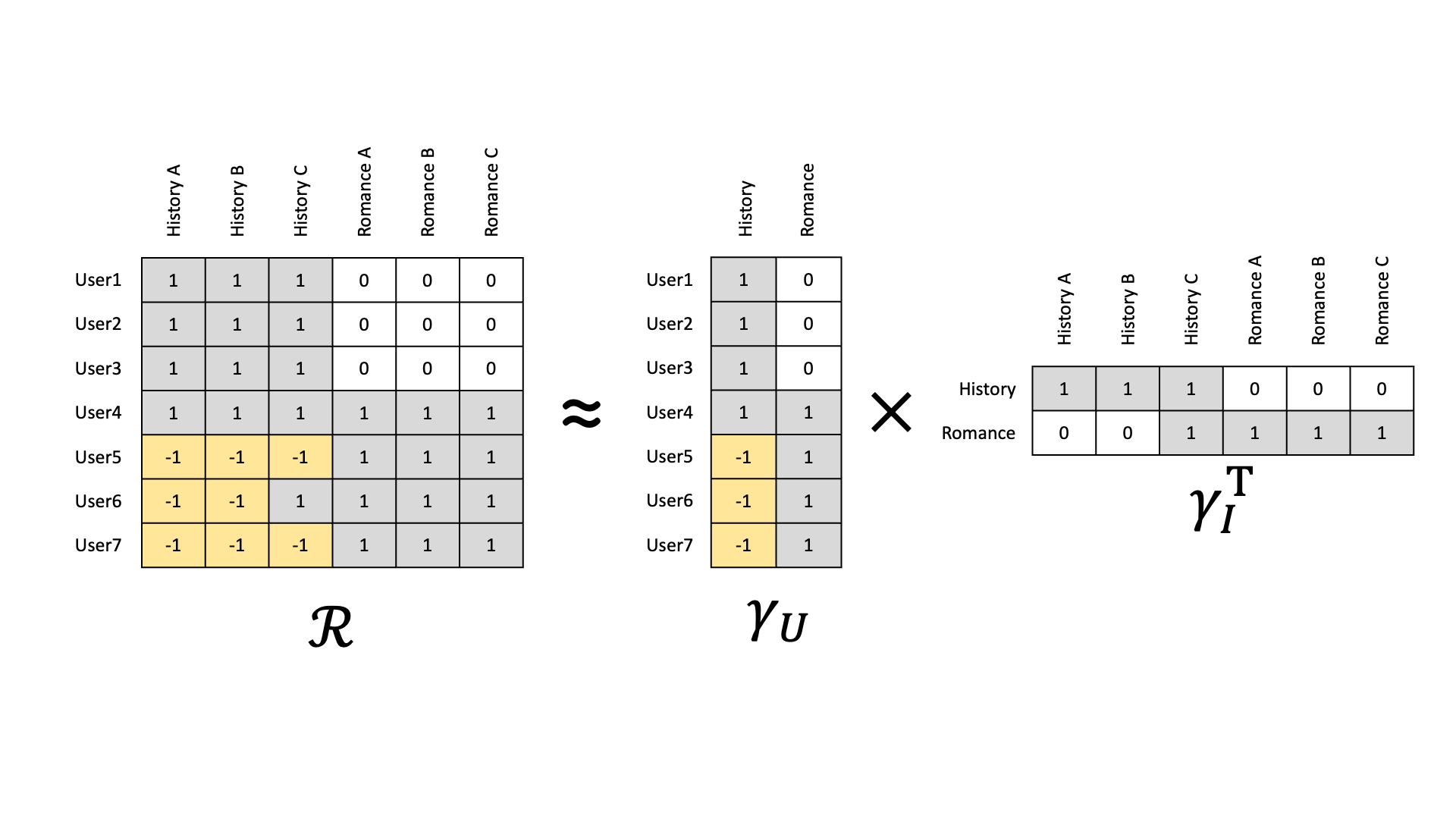
영화 아이템으로 역사를 다루는 영화와 로맨스 영화가 존재하고, 영화를 본 사용자에는 역사 영화만을 좋아하는 사용자, 로맨스만을 좋아하는 사용자, 그리고 둘 다 좋아하는 사용자에 관한 데이터가 $R$이라는 상호작용 행렬로 존재한다고 가정한다.

이때 latent factor model을 사용하면 각 사용자마다 어떤 장르를 좋아하는지에 관한 $\gamma_U$ 행렬, 각 아이템이 어떠한 장르에 해당되는지를 의미하는 $\gamma_I^T$ 행렬로 분해할 수 있다.

 

모델링하여 학습된 user latent factor, item latent factor를 같은 공간에 도식화할 경우, 데이터가 잠재적인 의미를 갖는 형태로 분포되는 것을 알 수 있다.

영화의 장르 정보를 제공하지 않더라도, 상호작용의 패턴을 통해서 이러한 잠재 정보를 발견할 수 있는 것이다.

 

[출처] https://arxiv.org/pdf/1401.5226.pdf, The Why and How of Nonnegative Matrix Factorization

 

Latent factor model로서의 MF는 추천 시스템에만 적용할 수 있는 것이 아니라, 차원 축소 테크닉으로서 이미지의 특징을 추출하거나 문서의 주제를 추출하는 용도로 다양한 데이터 타입에도 적용 가능하다.

 

 

 

Model-based CF를 사용한 Netflix Prize

 

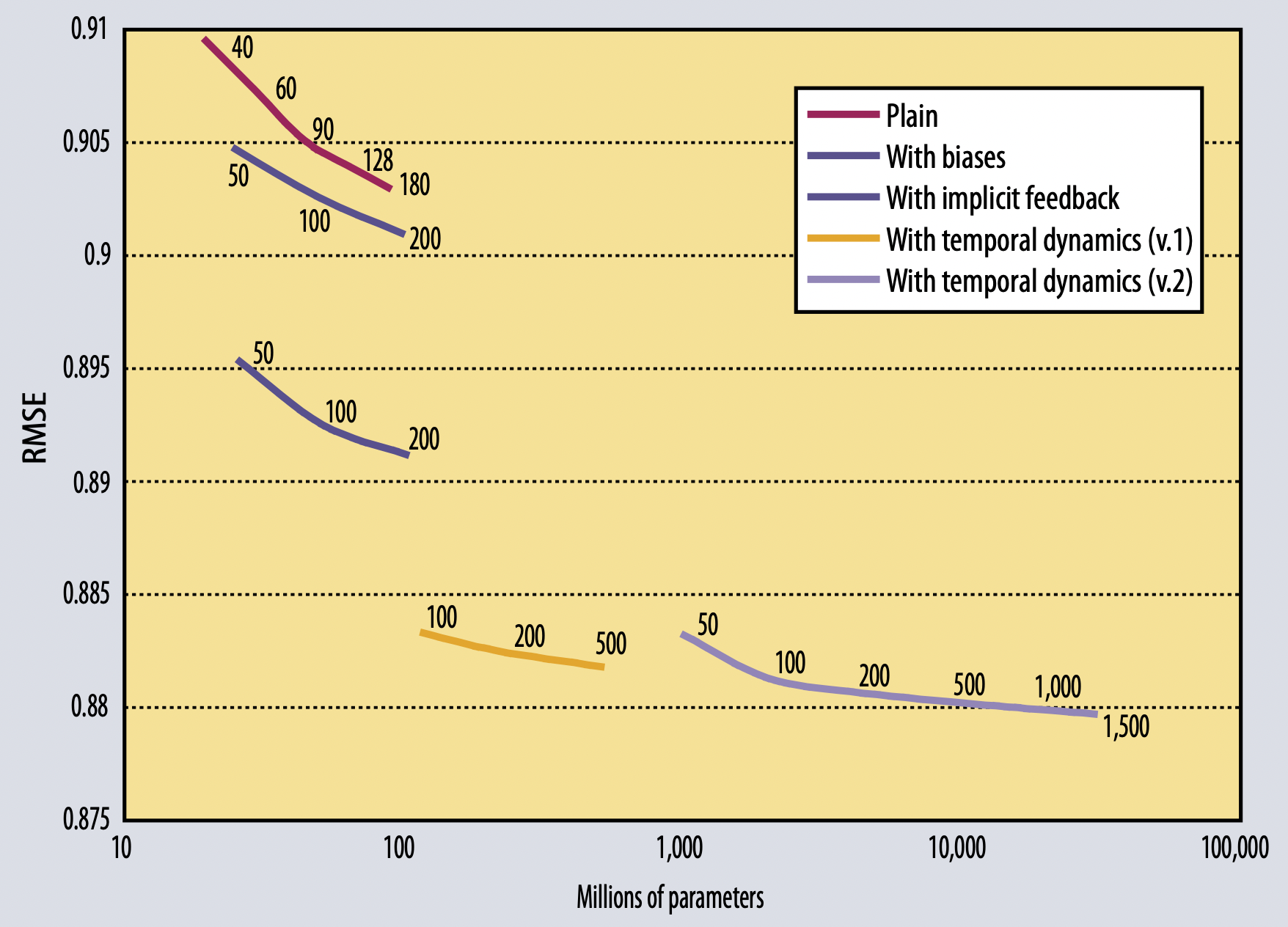
[출처] https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf, Matrix Factorization Techniques for Recommender System

 

Netflix Prize는 약 1억개의 영화 평점 데이터를 가지고 넷플릭스의 기존 알고리즘 대비 10% 이상 RMSE를 감소시킬 수 있으면 상금을 부여하는 대회였다.

이 데이터는 약 1만 7천개의 영화와 약 48만 명의 사용자로 이루어진 explicit feedback인 평점으로 이루어졌다.

결과적으로 MF 기반의 다른 기법들을 혼합한 Model-based CF 알고리즘이 우승을 했다.

 

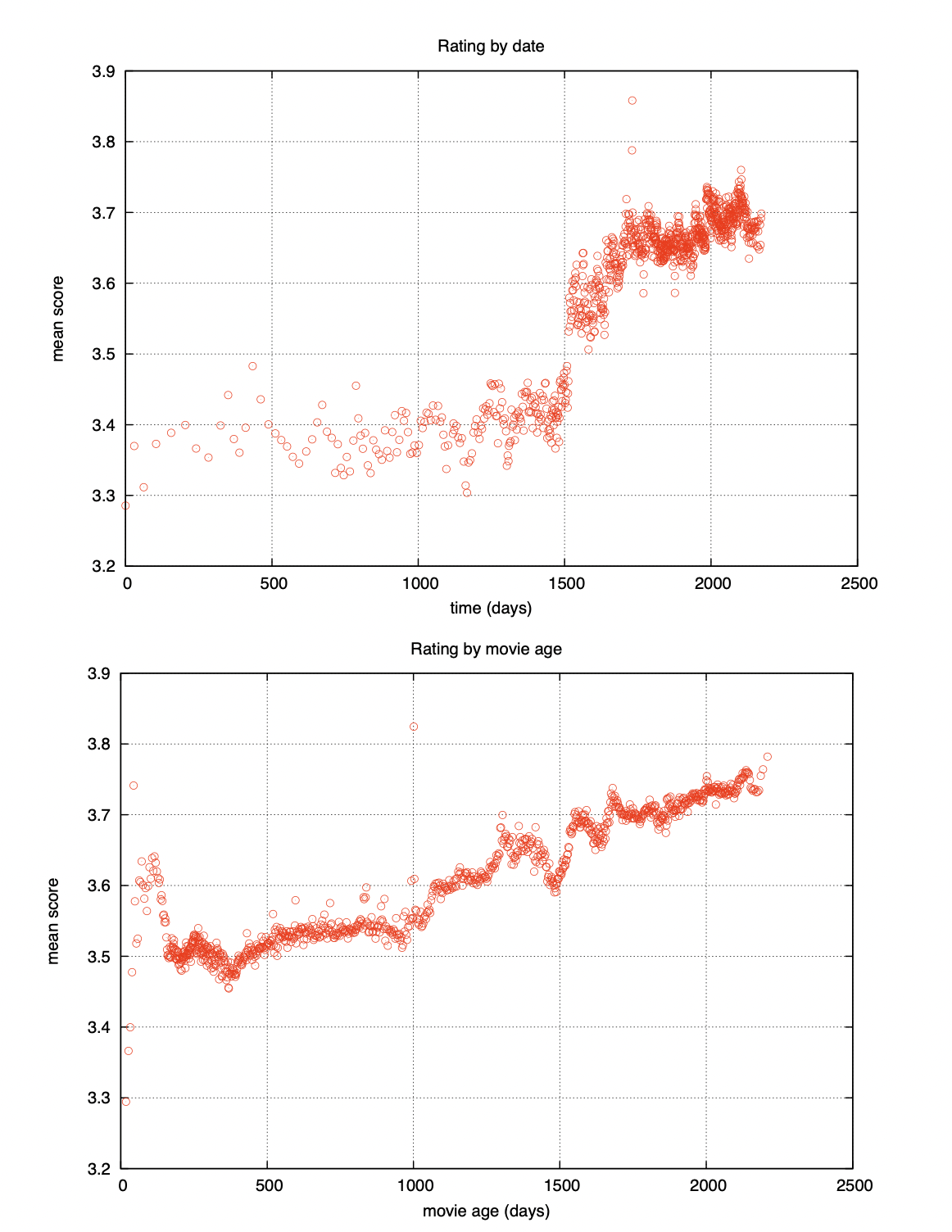
[출처] https://faculty.cc.gatech.edu/~zha/CSE8801/CF/kdd-fp074-koren.pdf, Collaborative Filtering with Temporal Dynamics

 

특히 Netflix 데이터 셋에서는 EDA로 발견한 Temporal Dynamics라는 요소가 매우 중요한 정보로 작용했으며, 성능 향상에 크게 기여했다.

여기서 이 Temporal Dynamics는 2004년 초에 Netflix 시스템의 변화로 평점 평균이 급격하게 증가하는 사건과 더불어 영화의 출시일로부터 시간이 흐를수록 평점이 증가하는 경향을 보이는 두 가지 요소를 의미한다.

 

출처
1. 네이버 커넥트재단 부스트캠프 AI Tech RecSys Track