추천 시스템의 핵심이 되는 여러 방법론

 

 

SOTA(State-Of-The-Art) 추천 시스템의 근간이 되는 방법론

 

앞서 참고로 여기서의 SOTA(State-of-The-Art)의 의미는 '최고의 성능을 내는' 정도로 해석하면 된다.

 

Matrix Factorization

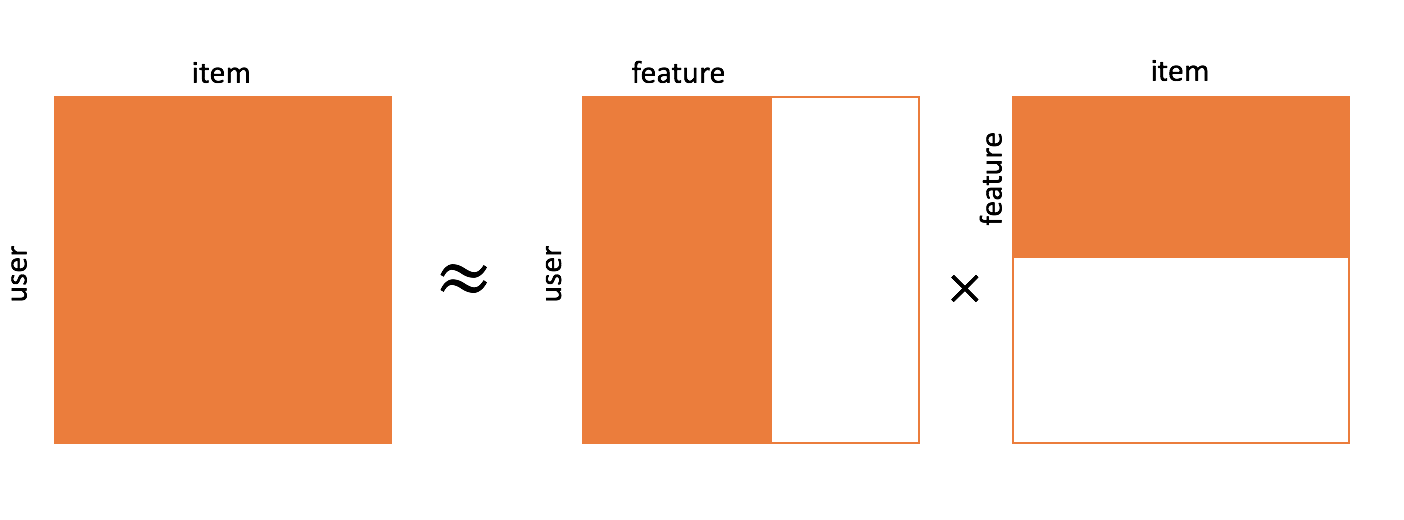
[출처] https://commons.wikimedia.org/wiki/File:Matrix_factorization.png, Xianteng

 

사용자와 아이템의 저차원 표현을 학습하는 것으로 볼 수 있으며, 명시적인 feature를 사용하지 않고도 잠재 표현을 학습하기 때문에 흔히 latent factor model이라고 부른다.

 

$$ R \approx \gamma_U \times \gamma_I^T $$

 

$R$: Sparse한 사용자와 아이템 상호작용 행렬

$\gamma_U$: 각 사용자의 선호도에 관한 잠재 벡터를 행벡터로 갖는 행렬

$\gamma_I^T$: 각 아이템의 속성에 관한 잠재 벡터를 열벡터로 갖는 행렬

 

사용자의 선호도 벡터와 아이템의 속성 벡터를 같은 공간상에 도식화했을 때, 공간의 각각의 축이 의미하는 바는 아이템의 카테고리, 사용자의 취향 등 잠재적인 의미를 갖는 축이 된다.

 

$$ R_{ui} \approx f(u, i) = \alpha + \beta_u + \beta_i + \gamma_u \cdot \gamma_i $$

 

사용자와 아이템 벡터를 내적하고 global bias term과 사용자와 아이템에 관한 bias term을 모두 더함으로써 사용자와 아이템 간의 상호작용인 평점을 예측하게 된다.

이를 통해 목적함수를 정의하면 다음과 같이 나타낼 수 있다.

 

$$ \frac{1}{\mathcal{J}} \sum_{(i, j) \in J} (f(u,i) - R{ij})^2 + \lambda \Omega(\beta, \gamma) $$

 

$\mathcal{J}$: 학습 데이터의 사용자와 아이템의 상호작용

$\lambda$: 정규화 파라미터

$\Omega$: 정규화 Term

 

MF는 explicit feedback(real-valued, $r_{ui} \in \mathbb{R}$)으로 이루어진 rating을 예측하는 데에도 쓰이지만, implicit feedback(binary outcome, $r_{ui} \in \{ 0, 1 \}$)으로 이루어진 데이터로부터 ranking을 수행하는 데에도 효과적이다.

 

Explicit feedback으로 평점을 예측할 때는 주로 RMSE를 최적화하는 optimizer를 사용하는 반면에, implicit feedback으로 Top-K ranking을 수행할 때는 RMSE로 최적화가 어려워서 주로 회귀나 클래스 분류의 방법으로 해결할 수 있다.

Explicit feedback은 사용자로부터 직접 평점을 입력하게 하여 데이터를 수집해야 하는 수고로움이 존재하고 사용자에게 불편함을 야기해서 많은 데이터를 수집하기 어려운 편이다.

 

반면에 사용자가 직접적으로 선호도를 표현하지는 않지만, 사용자가 어떠한 아이템을 클릭하고 상호작용(구매, 시청 등)을 했는지에 관한 다양한 데이터를 좀 더 쉽게 수집할 수 있어서 implicit feedback을 사용하여 추천 시스템을 활용하는 경우가 많다.

Matrix Factorization으로 Implicit feedback을 다룰 때는 행렬의 각 원소에 서로 다른 confidence 값을 부여하는 instance re-weighting scheme이 활용된다.

 

$r_{ui}$: 사용자 $u$가 영상 $i$를 클릭한 횟수

 

Positive instance(Preference)는 다음과 같이 정의할 수 있다.

 

$$ p_{ui} = \begin{cases} 1 & \mbox{if } r_{ui} >0 \\ 0 & \mbox{otherwise } \end{cases} $$

 

사용자 $u$가 아이템 $i$를 선호하는 정도를 의미하는 Confidence 값은 다음과 같이 정의할 수 있다.

 

$$ c_{ui} = 1 + \alpha r_{ui} \quad \text{ OR } \quad c_{ui} = 1 + \alpha \log(1 + \frac{r_{ui}}{\epsilon}) $$

 

이를 통해 목적함수를 다음과 같이 정의할 수 있다.

 

$$ \underset{\gamma}{\arg \min} \sum_{(u, i) \in \mathcal{J}} c_{ui} (p_{ui} - \gamma_u \cdot \gamma_i)^2 + \lambda \Omega(\gamma) $$

 

위와 같은 목적함수를 정의하는 방법을 Weighted Regularized MF 또는 Weighted MF라고 한다.

 

 

 

Bayesian Personalized Ranking(BPR)

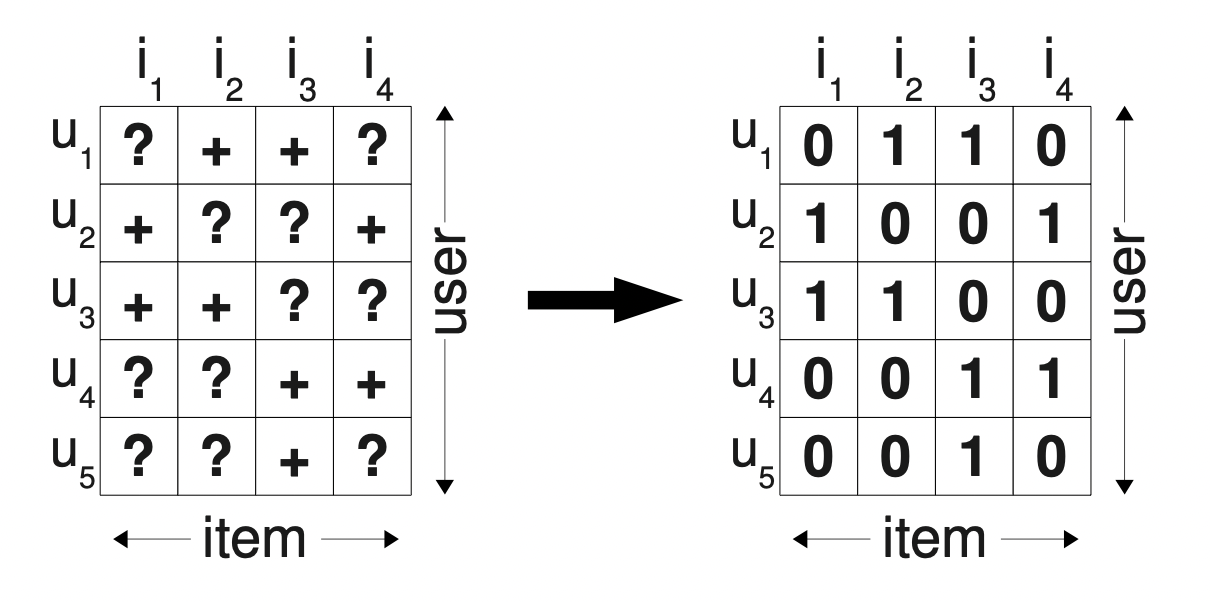
[출처] https://arxiv.org/pdf/1205.2618.pdf?source=post_page, BPR: Bayesian Personalized Ranking from Implicit Feedback

 

BPR은 사용자의 선호도를 두 아이템 간의 pairwise-ranking 문제로 formulation 함으로써 각 사용자 $u$의 personalized ranking function($i >_u j$)을 추정한다.

이를 통해 기존의 implicit feedback을 다뤘던 방법론의 한계를 극복하려고 한다.

기존 방법들은 missing value를 0으로 처리했고, 결과적으로 선호하지 않은 아이템과 사용자가 아직 접하지 않았지만 선호할만한 아이템이 0에 섞이게 되어 regression objective를 사용하면 사용자가 선호할 수 있지만 아직 보이지 않은 아이템(unseen item)에 negative scoring을 부여하는 경우가 발생할 수 있기 때문이다.

그래서 BPR에서는 단순히 0과 1이 아니라 positive instance에는 높은 score를 주고 non-positive instance에는 낮은 score를 주어 ranking하는 형태로 바꾸는 아이디어를 택한다.

 

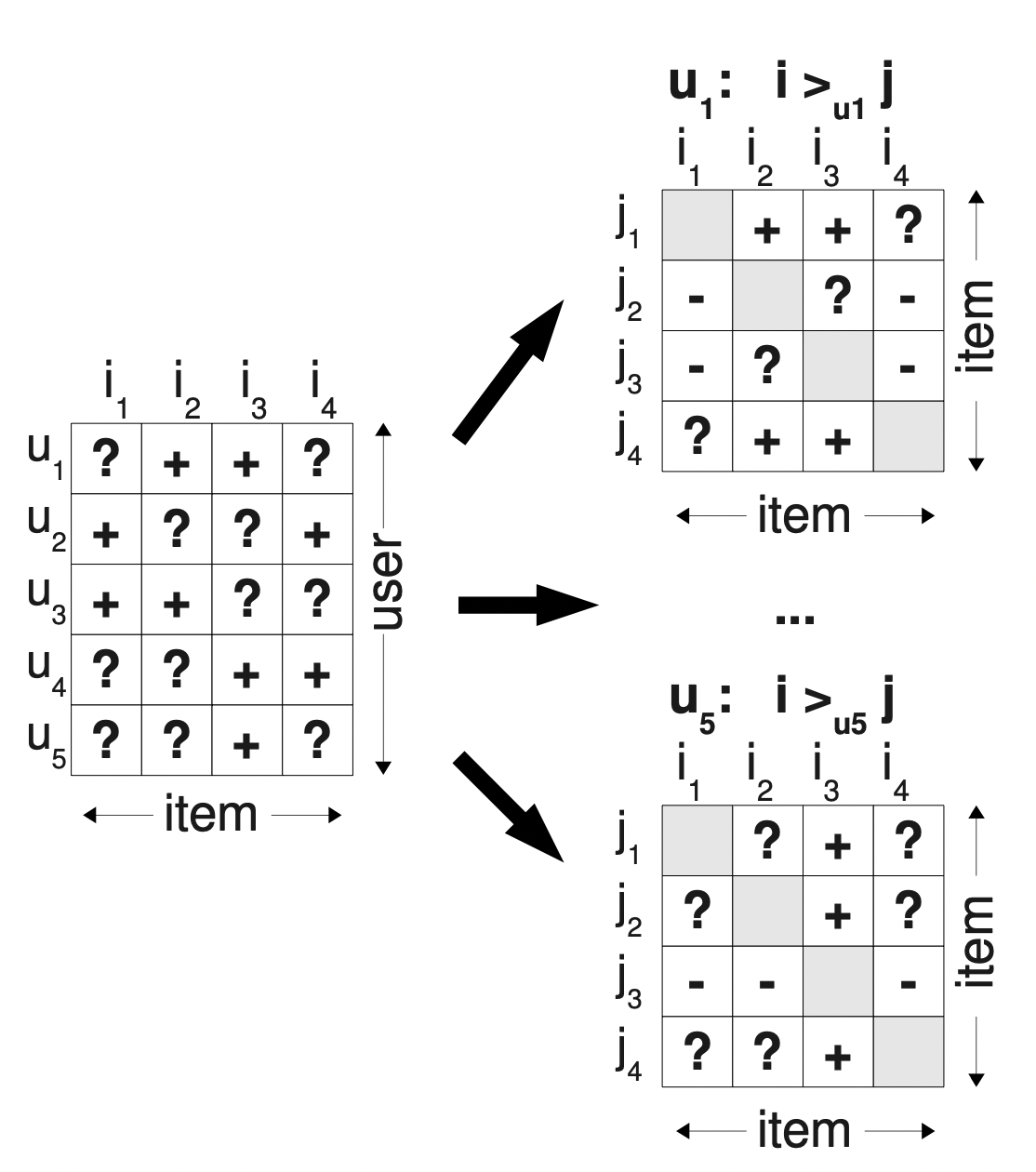
[출처] https://arxiv.org/pdf/1205.2618.pdf?source=post_page, BPR: Bayesian Personalized Ranking from Implicit Feedback

 

$i >_u j$: "사용자 $u$가 아이템 $j$보다는 $i$를 더 선호한다"를 의마하는 personalized ranking function이다.

$\hat{x}_{uij}$: $i >_u j$를 추정하기 위해 도입한 pairwise preference를 나타내는 parameteric predictor이다.

 

$\hat{x}_{uij} > 0$이면 사용자 $u$가 아이템 $i$를 좋아하는 것이다.

$\hat{x}_{uij} \le 0$이면 사용자 $u$가 아이템 $j$를 좋아하는 것이다.

 

$$ p(i>_u j | \Theta) := \sigma \left( \hat{x}_{uij}(\Theta) \right) $$

 

위의 식은 파라미터 $\Theta$가 주어졌을 때, 사용자 $u$가 아이템 $i$를 아이템 $j$에 비해 더 좋아할 확률을 뜻한다.

$p(\Theta) \sim N(0, \mathit{\Sigma_{\Theta}}) $처럼 파라미터 $\Theta$에 대한 사전확률이 Gaussian 분포를 따른다고 가정하고, 사후 확률을 최대화하기 위한 Maximum a Posterior(MAP) Estimator를 사용하여 아래와 같이 personalized ranking objective function을 정리하면 다음과 같다.

 

$$ \begin{aligned} \text{BPR-Opt} :=& \ln p(\Theta| >_u)\\ =& \ln p(>_u|\Theta) p(\Theta)\\ =& \ln \underset{(u, i, j) \in D_S}{\prod} \sigma \big{(} \hat{x}_{uij}(\Theta) \big{)} p(\Theta)\\ =& \underset{(u,i,j) \in D_S}{\sum} \ln \sigma \big{(} \hat{x}_{uij}(\Theta) \big{)} + \ln p(\Theta)\\ =& \underset{(u,i,j) \in D_S}{\sum} \ln \sigma \big{(} \hat{x}_{uij}(\Theta) \big{)} - \lambda_{\Theta} \|\Theta\|^2 \end{aligned} $$

 

결과적으로 $\hat{x}_{uij}$가 어떠한 형태를 따르는지에 따라서 이 BPR의 전체 objective function의 형태가 결정된다.

가장 단순한 형태로는 이 $\hat{x}_{uij}$를 정의할 때 $\hat{x}_{uij} = \hat{x}_{ui} - \hat{x}_{uj}$처럼 사용자 $u$의 아이템 $i$에 대한 선호도와 아이템 $j$에 대한 선호도의 차이로 나타낼 수 있다.

이때 각 compatibility function에 해당되는 $\hat{x}_{ui}$와 $\hat{x}_{uj}$는 latent factor model의 결과값으로 정의될 수 있다.

 

$$ \hat{x}_{uij} = \hat{x}_{ui} - \hat{x}_{uj} = \gamma_u \cdot \gamma_i - \gamma_u \cdot \gamma_j $$

 

MF에서는 하나의 item에 관한 어떤 pointwise한 optimization을 수행하는 반면에, BPR은 두 아이템을 서로 비교하는 pairwise optimization을 수행한다.

또한 explicit feedback로 MF를 사용하는 관점에서 MF는 MSE를 직접 최적화하는 regression이지만, BPR은 분류 문제를 푸는 것으로 이해할 수 있다.

 

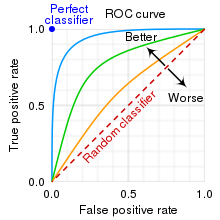
[출처] https://en.wikipedia.org/wiki/File:Roc_curve.svg, cmglee, MartinThoma

 

BPR의 objective function을 최적화하는 것이 흔히 쓰이는 metric의 하나인 AUC(Area Under ROC Curve) 값을 최적화하는 것과 이론상으로 동일하다는 주장이 있다.

분류 문제에서 AUC 값은 분류기가 임의의 positive와 negative sample이 주어졌을 때, negative sample보다 positive sample을 더 높은 순위(더 높은 positive 확률)로 평가할 확률을 의미한다.

 

$$ \text{AUC}(u) = \frac{1}{|I_u||I \setminus I_u|} \sum_{i \in I_u} \sum_{j \in I \setminus I_u} \delta(x_{u,i,j} > 0) $$

 

사용자 별 AUC인 $\text{AUC}(u)$는 BPR에 의해 올바르게 ranking된 케이스의 비율을 나타낸다.

$\delta(x_{u,i,j} > 0)$는 BPR에 의해 알맞게 ranked된 케이스를 뜻한다.

 

 

 

Factorizing Personalized Markov Chains(FPMC)

 

FPMC는 MF와 Markov Chain(MC; sequential behaviors)을 결합한 모델로 사용자와 아이템 간의 관계, 그리고 아이템과 바로 이전 아이템 간의 관계를 함께 모델링한다.

$$ f(u, i) + f(i, i^{(prev)}) $$

 

Markov property는 다음 스텝의 상태는 이전의 상태에만 영향을 받는다는 것을 의미한다.

보통 first-order인 바로 직전 상태에만 영향을 받는 것을 뜻하며, $AR(1)$ 모델이 그 예시이다.

 

$$ p(i^{(t)} = i | i^{(t-1)}, \cdots, i^{(1)}) = P(i^{(t)} = i|i^{(t-1)}) $$

 

FPMC는 사용자 별로 개인화된 형태의 user-specific Markov Chain을 가정한다.

 

$$ p(i_u^{(t)} = i | i_u^{(t-1)}, \cdots, i_u^{(1)}) = P(i_u^{(t)} = i|i_u^{(t-1)}) $$

 

사용자 별로 이전 step과 현재 step의 전이 확률이 다를 수 있음을 반영한다고 이해할 수 있다.

 

편의상 이전 아이템을 $j$라고 하면 아래와 같은 함수를 fitting하는 문제로 표현될 수 있다.

 

$$ f(i|u,j), \mbox{ where } u \mbox{ is a user, } i \mbox{ is a next item to be recommended, and } j \mbox{ is a previous item } $$

 

이전에는 $f(u, i)$라는 2차원 관계만을 다루고 있었지만, FPMC에서는 이전 아이템을 의미하는 $j$가 추가되어 원소별로 전이 확률(transition probability)를 지니는 sparse한 3-way tensor($|U| \times |I| \times |I|)$로 표현될 수 있다.

 

$$ f(i|u,j) = r_u^{U,I} \cdot r_i^{I, U} + r_i^{I, J} \cdot r_j^{J, I} + r_u^{U,J} \cdot r_j^{J, U} $$

 

$r_u^{U,I} \cdot r_i^{I, U}$: 사용자와 다음 아이템의 compatibility

$r_i^{I, J} \cdot r_j^{J, I}$: 이전 아이템과 다음 아이템의 compatibility

$r_u^{U,J} \cdot r_j^{J, U}$: 사용자와 이전 아이템의 compatibility

 

위의 식을 BPR-like framework를 도입하여 최적화를 수행하면 다음과 같이 나타낼 수 있다.

 

$$ \sigma(f(i|u,j) - f(i^{-}|u, j)), \mbox{ where } i^{-} \mbox{ is a sampled non-consumed negative item } $$

$$ f(i|u,j) - f(i^{(-)|u, j}) = (r_u^{U,I} \cdot r_i^{I, U} + r_i^{I, J} \cdot r_j^{J, I}) + (r_u^{U,I} \cdot r_{i^{(-)}}^{I, U} + r_{i^{(-)}}^{I, J} \cdot r_j^{J, I}) $$

 

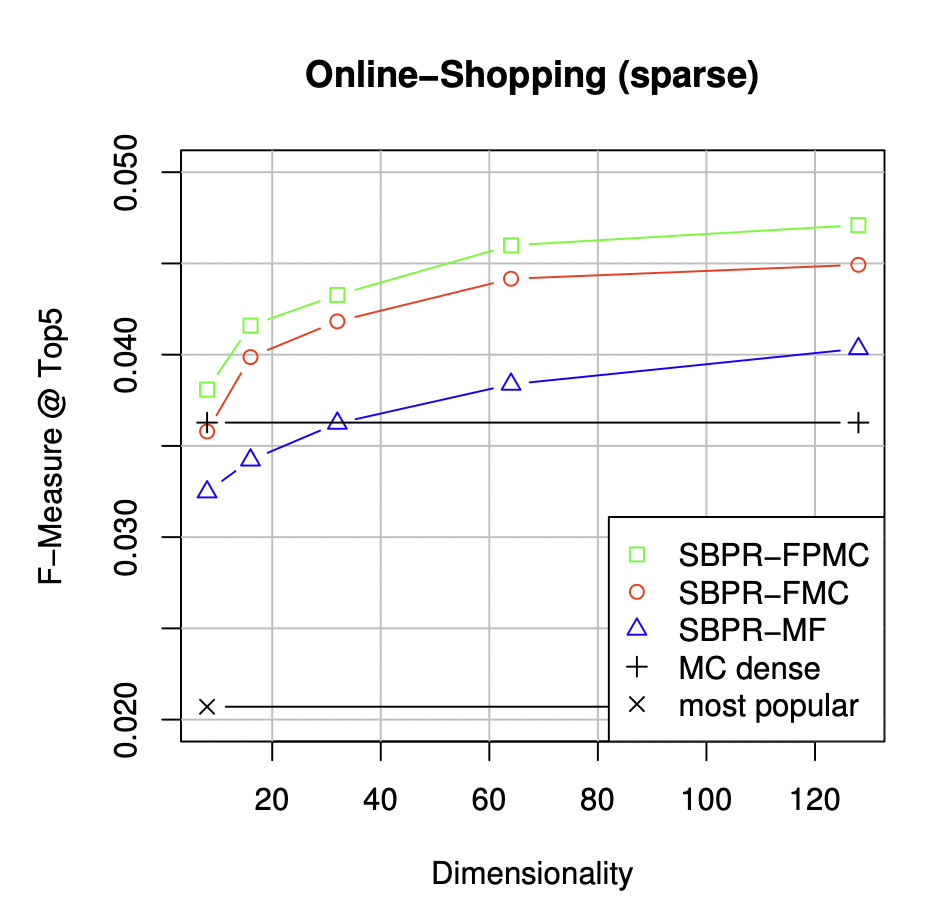
[출처] https://www.ra.ethz.ch/CDStore/www2010/www/p811.pdf, Factorizing Personalized Markov Chains for Next-Basket Recommendation

 

F@5 측정 결과 FPMC에서 사용자 factor를 제거한 FMC, MF보다 FPMC가 상대적으로 더 좋은 성능을 보인다고 한다.

 

 

 

Personalized Ranking Metric Embedding(PRME)

 

PRME는 compatibility function으로 inner product가 아닌 metric space에서 Euclidean distance 같은 다른 distance metric을 사용한다.

즉, $\gamma_u \cdot \gamma_i$ 대신 $d(\gamma_u \cdot \gamma_i)$를 사용하는 것이다.

 

사용자의 순차적인 check-in 기록을 바탕으로 다음에 방문할 곳을 예측하는 태스크인 Next POI(Point-of-Interest) 추천 시스템에서 활용할 수 있다.

또한 인접한 유사 장르의 음악을 추천하는 playlist prediction과 같은 음악 도메인의 태스크에도 효과적이다.

 

$$ \text{PRME}: f(i|u,j) = -d(\gamma_u, \gamma_i)^2 - d(\gamma_i, \gamma_j)^2 $$

 

여기서 $\gamma$는 실제 geographical location이 아니라 latent space에서 정의된 것임을 유의한다.

 

$$ f(i|u,j) = -\|\gamma_u, \gamma_i\|_2^2 - \|\gamma_i, \gamma_j\|_2^2 $$

 

Inner product를 활용하면 사용자가 원하는 아이템의 특징이 극단적인 것까지 아이템으로 추천될 수 있는 반면에, Euclidean 거리 같이 nearest neighbor를 활용하면 사용자가 원하는 아이템의 특징과 유사한 것들만 추천할 수 있게끔 할 수 있다.

 

출처
1. 네이버 커넥트재단 부스트캠프 AI Tech RecSys Track