Multi-Armed Bandit이란?

카지노에 있는 슬롯머신은 한 번에 한 개의 arm을 당길 수 있다. (One-Armed Bandit)
만약에 카지노에 있는 K개의 슬롯머신을 N번 플레이할 수 있으면 어떻게 플레이 하는 것이 좋을지에 관한 아이디어에서 나온 것이다.
K개의 슬롯머신에서 얻을 수 있는 reward의 확률이 모두 다르다고 가정한다.
Reward를 최대화하기 위해서는 arm을 어떠한 순서로 또는 어떤 정책에 의해 당겨야 하는지를 구하는 것이 문제이다.
Multi-Armed Bandit의 문제
그러나 슬롯머신의 reward 확률을 정확히 알 수 없다는 것이 단점이다.
모든 슬롯 머신을 동일한 횟수로 당기면 높은 reward를 얻을 수 없게 된다. (Exploration)
일정 횟수만큼 슬롯머신을 당겨보고, 남은 횟수는 그 시간동안 제일 높은 확률을 가진 슬롯머신만 당기면 동일한 슬롯만 계속 당기게 될 수 있다. (Exploitation)
그래서 Exploration과 Exploitation Trade-off 문제가 발생한다.
Exploration & Exploitation Trade-off
Exploration(탐색)
더 많은 정보를 얻기 위해 새로운 arm을 선택하는 것이다.
Exploitation(활용)
기존의 경험 또는 관측 값을 토대로 가장 좋은 arm을 선택하는 것이다.
Exploration(탐색)이 너무 많은 경우는 exploitation(활용)이 너무 적은 경우와 같은데, 이떄는 탐색에 비용을 지나치게 낭비하여 높은 reward를 얻을 수 없다.
Exploration(탐색)이 너무 적은 경우는 exploitation(활용)이 너무 많은 경우와 같은데, 이때는 잘못된 슬롯머신을 활용하게 되면 높은 reward를 보장할 수 없다.
Multi-Armed Bandit 공식
$$ q_{*}(a) \doteq \mathbb{E}[R_t | A_t = a] $$
$t$: time step 또는 play number
$A_t$: 시간 $t$에 play한 action
$R_t$: 시간 $t$에 받은 reward
$q_{*}(a)$: 액션 $a$에 따른 reward의 실제 기댓값
여기서의 액션은 어떤 한 슬롯머신을 당기는 행위를 의미한다.
최종적으로 알고 싶은 것은 각각의 액션에 관하여 실제 reward의 기댓값이다.
모든 action에 대한 $q_{*}(a)$를 정확히 알고 있으면 문제를 해결할 수 있다.
그러나 실제 reward의 true distribution을 모르기 때문에 추정을 해야한다.
$q_{*}(a)$에 대한 시간 $t$에서의 추정치 $Q_t(a)$를 최대한 $q_{*}(a)$와 비슷하도록 정밀하게 구하는 것이 목표이다.
매 time step마다 추정 가치가 최대인 action을 선택하는 것이 greedy action이다.
Greedy action을 선택하는 것은 exploitation이고, 다른 action을 선택하는 것은 exploration이다.
Multi-Armed Bandit 알고리즘
Simply Average Method(Greedy Algorithm)
$$ Q_t(a) \doteq \frac{\text{sum of rewards when } a \text{ taken prior to } t}{\text{number of times } a \text{ taken prior to }t } = \frac{\sum_{i=1}^{t-1} R_i \cdot 1_{A_i = a}}{\sum_{i=1}^{t-1} 1_{A_i = a}} $$
실제 기댓값인 $q_{*}(a)$의 가장 간단한 추정 방식으로 표본 평균을 사용한다.
즉, 지금까지 관측된 개별 슬롯머신의 reward의 평균값을 구하는 것이다.
액션 $a$를 수행하면서 얻은 reward의 총합을 분자로, 액션 $a$를 수행한 총 횟수를 분모로 하여 계산하면 된다.
가장 간단한 policy로서 평균 리워드가 최대인 action을 선택하는 것이므로 greedy한 방식이다.
$$ A_t = \underset{a}{argmax} Q_t(a) $$
문제는 policy가 처음에 선택되는 action과 reward에 크게 영향을 받아서 exploration이 부족하다.
Epsilon-Greedy Algorithm
Exploration이 부족한 greedy algorithm의 policy를 수정한 전략이다.
일정한 확률에 의해 랜덤으로 슬롯머신을 선택하도록 하고, 그외의 확률은 greedy하게 슬롯머신을 선택한다.
$$ A_{t}= \begin{cases} \underset{a}{\text{argmax }}Q_t(a) & \mbox{ with probability } 1 - \epsilon \\ \text{a random action} & \mbox{ with probability } \epsilon \end{cases} $$
Exploration과 exploitation을 어느 정도 보장하는 단순하면서도 강력한 알고리즘이어서 MAB 기법을 비교할 때 baseline으로 많이 사용한다.
그러나 time step이 많이 지나고 데이터가 충분히 쌓여서 각각의 액션의 true distribution을 추정할 수 있으면 epsilon-greedy algorithm을 사용하는 건 손해를 볼 수 있다.
Upper Confidence Bound(UCB)
$$ A_t \doteq \underset{a}{argmax} \left[ Q_t(a) + c \sqrt{\frac{\ln t}{N_t(a)}} \right] $$
$t$: time step 또는 play number
$Q_t(a)$: 시간 $t$에서 액션 $a$에 대한 reward 추정치 (simple average)
$N_t(a)$: 액션 $a$를 선택했던 횟수
$c$: exploration을 조정하는 하이퍼 파라미터
Simple average로 사용하는 표본 평균에다가 term을 추가해서 exploration이 잘 될 수 있도록 한다.
새로 추가된 term은 해당 action이 최적의 action이 될 수도 있는 가능성인 불확실성을 표현한 것이다.
지금까지 관측값에서 액션 $a$가 많이 선택되지 않으면 분모의 값이 낮을 것이고, 이럴 경우 불확실성의 term 값이 커져서 시간 $t$에 해당 action을 선택할 가능성이 높아질 수 있다.
시간이 지날수록 전반적인 액션들의 선택 횟수가 늘어날 것이고, $\ln t$값의 증가 폭은 줄어들면서 $c \sqrt{\frac{\ln t}{N_t(a)}}$인 불확실성의 term이 0으로 수렴한다.
MAB 알고리즘의 파라미터 튜닝
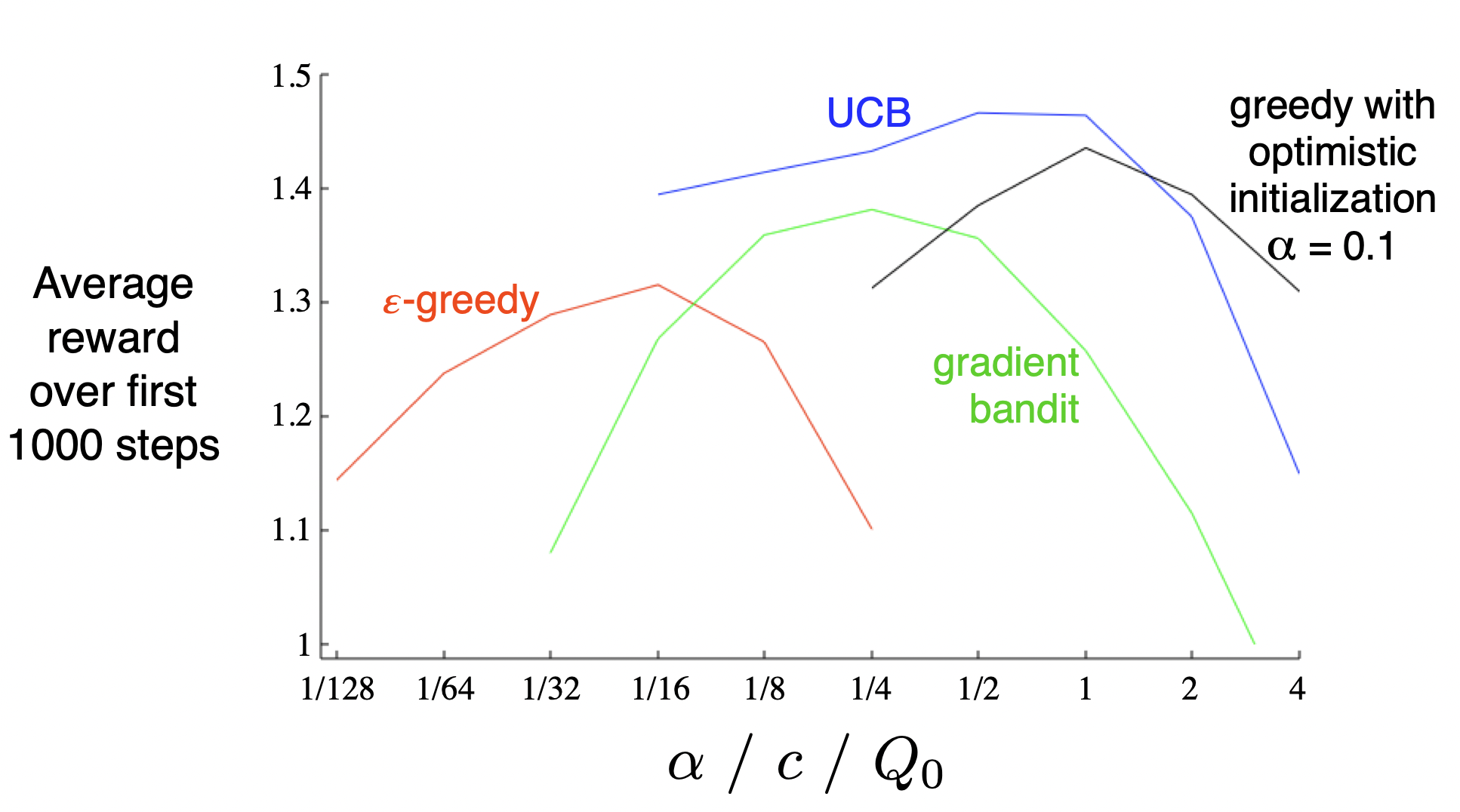
[출처] https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf
각각의 알고리즘을 사용할 때는 적절한 하이퍼 파라미터를 찾아서 exploration과 exploitation의 trade-off가 고려되도록 한다.
Multi-Armed Bandit의 추천 예시
Multi-Armed Bandit을 이용한 추천 시스템
Bandit 문제에서는 실제 서비스의 지표인 클릭 또는 구매를 모델의 reward로 가정한다.
해당 reward를 최대화하는 방향으로 모델이 학습되고 추천을 수행한다.
무거운 추천 모델을 사용하지 않고 간단한 Bandit 기법을 적용해도 온라인 지표가 좋아지는 장점이 있다.
추천하는 개별 아이템은 개별 action에 해당되고, 이 개별 아이템을 유저가 선택 또는 클릭할 확률을 예측하는 것이다.
유저가 아이템을 추천하는 방식이 MAB의 policy에 해당되고, 아이템을 추천했을 때 유저의 클릭 여부를 reward로 측정한다.
구현이 간단하고 이해하기 쉬워서 실제 비즈니스 어플리케이션에 매우 유용하다.
유저 추천
개별 유저에 관해서 모든 아이템의 Bandit을 구하는 것은 불가능하다.
개인별로 구축하기에는 데이터가 부족하여 Bandit이 수렴하지 않는다.
그래서 Clustering을 통해 비슷한 유저끼리 그룹화한 뒤 해당 그룹 내에서 Bandit을 구축한다.
Cluster 별로 아이템 후보 리스트를 생성하며, 인기도 기반, CF 등의 다양한 방법을 사용할 수 있다.
결국 필요한 Bandit 개수는 유저 클러스터 개수에 후보 아이템 수를 곱한 값이 될 것이다.
유사 아이템 추천
주어진 아이템과 유사한 후보 아이템 리스트를 생성하고, 그 안에서 Bandit을 적용한다.
유사 아이템 추출 방법에는 MF, Item2Vec 기반의 유저-아이템 상관관계를 기반으로 한 유사도를 구하거나 이미지 feature, 텍스트 feature 등 Content-Based 기반의 유사도를 구하는 방법이 있을 것이다.
결국 필요한 Bandit it 개수는 전체 아이템 개수마다 각 아이템의 유사한 후보 아이템 개수를 더한 것이 된다.
출처
1. 네이버 부스트캠프 AI Tech 추천시스템 Stage 2 기초 강의