[빠르게 정리하는 선형대수] 행렬(Matrix)과 역행렬, 그리고 Positive Definite
- -
행렬은 선형대수에서 수를 다룰 때 자주 사용하는 형태이며, 기본적으로 AI 모델의 코드는 tensor 기반의 PyTorch로 작성하는 경우가 많아서 행렬에 관한 명확한 이해를 바탕으로 이를 자유자재로 다룰 줄 아는 능력이 중요하다. 행렬에 관한 기본적인 내용과 함께 정방행렬일 때의 역행렬과 정방행렬이 아닐 때 사용하는 pseudo 역행렬에 관해 알아보자.
행렬 (Matrix)
행렬의 정의
행렬의 정의는 다음과 같이 정의할 수 있다.
- 벡터(vector)를 원소로 가지는 2차원 배열
- 같은 차원의 벡터를 모아 나열한 것
즉, 행렬은 Vector를 원소로 가지는 2차원 list나 array이다.
numpy에서는 행 Vector를 기본단위로 생각한다.
행렬은 $n$개의 Vector를 가지고, Vevtor는 $m$개의 element를 가진다
행렬의 표현
- 행렬은 $\mathbf{X}$로 표현된다
- 행렬의 element인 Vector는 $[\mathbf{x_1}, \mathbf{x_2}, ... , \mathbf{x_n}]$과 같이 표현한다.
- 행렬의 $n$번째 Vector이면서, $m$번째 element는 $x_{nm}$으로 표현한다.
행렬의 이해
- 행렬은 행과 열이라는 두 개의 인덱스를 지니고 있다고 볼 수 있다.
- 또한 $m$차원 공간에서의 $n$개의 점으로 이루어진 데이터의 집합으로 이해할 수도 있다.
- 즉, $i$번째 데이터의 $j$번째 변수의 값을 구하는 데 사용할 수 있다.
- 특정 행 또는 열을 고정하면 행벡터 또는 열벡터로 이해할 수 있다.
이러한 이해 방식은 Broadcasting이나 Element-wise Operation 등으로 데이터를 조작하는데 유용하게 사용될 수 있다.
전치행렬(Transpose Matrix)
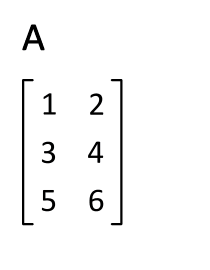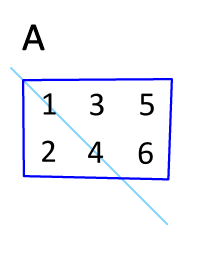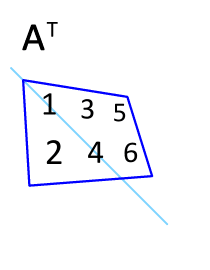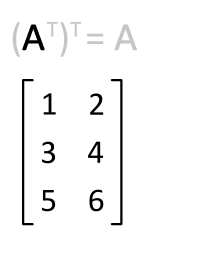
행렬 $A$의 행과 열 인덱스를 바꾸면 전치행렬 $A^T$을 구할 수 있다.
$A$: m x n 행렬 → $A^T$: n x m 행렬 $x_{ij}$ → $x_{ji}$
행렬의 연산
행렬의 덧셈과 뺄셈

[출처] https://commons.wikimedia.org/wiki/File:Matrix_addition_qtl2.svg, Quartl
같은 차원을 지닌 행렬은 서로 대응되는 원소끼리 덧셈과 뺄셈이 가능하다.
행렬의 곱셈
$\mathbf{X}\mathbf{Y}$와 같은 행렬의 곱셈은 $\mathbf{X}$의 i번째 행 벡터와 $\mathbf{Y}$의 j번째 열 벡터의 내적을 성분으로 갖는 행렬을 구하는 연산이다.
그래서 행렬의 곱셈 연산이 성립하려면 $\mathbf{X}$의 행벡터의 element와 $\mathbf{Y}$의 열벡터의 element의 수가 동일해야한다.
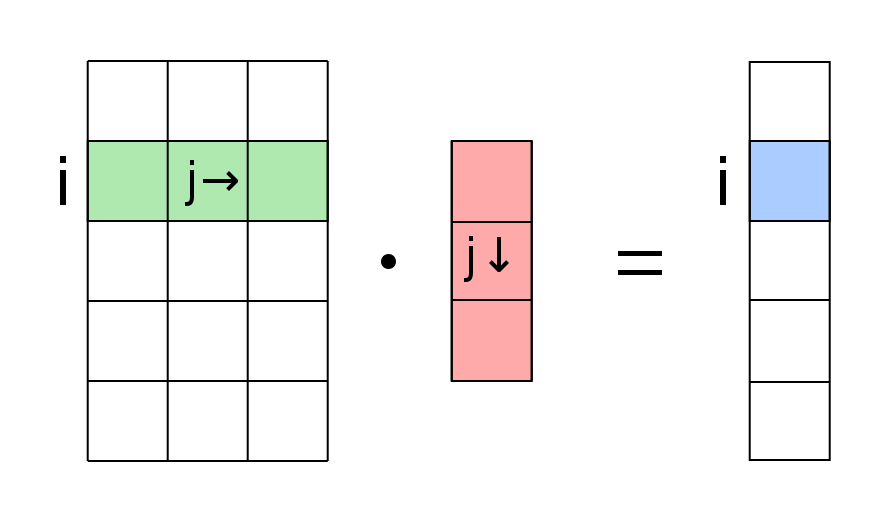
[출처] https://commons.wikimedia.org/wiki/File:Matrix_vector_multiplication.svg, Quartl
$\mathbf{X}$ 행렬의 행의 수 $=$ $\mathbf{Y}$ 행렬의 열의 수
행렬의 곱셈은 결합 법칙과 분배 법칙이 성립 가능하다.
하지만 교환 법칙은 성립하지 않아서 곱셈 순서에 따라 계산 결과가 달라지므로 $\mathbf{X}\mathbf{Y}$와 $\mathbf{Y}\mathbf{X}$는 전혀 다른 의미를 갖는다.
numpy에서 행렬의 곱셈은 @ 기호를 사용한다.
np.inner는 두 행 벡터를 대상으로 수행되며, 수학적으로는 뒤에 오는 벡터를 전치하여 내적한 값을 반환한다.
즉, np.inner(X, Y)는 $\mathbf{X}\mathbf{Y}^T = \left( \sum_{k}{x_{ik}y_{kj}} \right)$와 동일하며, 수학에서 말하는 내적과는 다르므로 유의한다.
일반적으로 행렬 곱셈이 i번째 행과 j번째 열벡터의 내적이라면, numpy의 내적은 i번째 행벡터와 j번째 행벡터의 내적이다.
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
Y = np.array([[0, 1, -1],
[1, -1, 0]])
Z = np.inner(X, Y)
print(Z)
'''
출력 결과
array([[ -5, 3],
[ 5, 2],
[ -3, -1]])
'''
행렬의 스칼라배는 행렬의 모든 성분에 같은 수를 곱하는 것이며, 벡터의 스칼라배와 유사하다.
행렬의 종류
| 행렬명 | 정의 |
| 영행렬(Zero Matrix) | 행렬의 성분 전체가 0인 행렬 |
| 정방행렬(Square Matrix) | 행과 열의 크기가 같은 행렬 |
| 대각행렬(Diagonal Matrix) | 정방행렬에서 대각 성분이 모두 0이 아니고, 나머지 성분이 0인 행렬 |
| 단위행렬(= 항등행렬, Identity Matrix) | 대각행렬 중 대각 성분이 1로만 구성된 행렬 |
| 상삼각행렬(Upper Triangular Matrix) | 대각선을 기준으로 위쪽에만 원소 값이 존재하는 행렬 |
| 하삼각행렬(lower Triangular Matrix) | 대각선을 기준으로 아래쪽에만 원소 값이 존재하는 행렬 |
| 대칭행렬(Symmetric Matrix) | 대각 원소에 대하여 대칭인 원소가 서로 같은 행렬 |
벡터 공간과 행렬
행렬은 Vector 공간에서 사용되는 연산자로서 이해할 수 있다.
행렬곱셈을 통해 $m$차원의 공간에 있던 $\mathbf{x}$를 $n$차원 공간의 $\mathbf{z}$로 변환할 수 있다는 의미이다.
즉, 차원을 이동시켜주는 함수이자 수식의 역할을 할 수 있고, 이를 통해 패턴추출이나 데이터 압축 등의 기능을 수행할 수 있다.
수학의 모든 선형 변환은 행렬곱으로 계산할 수 있다.
역행렬(Inverse Matrix)
행렬식
2차원 행렬 $A$에 관한 행렬식은 다음과 같이 정의한다.
$A = [[a, b], [c, d]]$ $|A| = det A = ad - bc$
역행렬의 의미
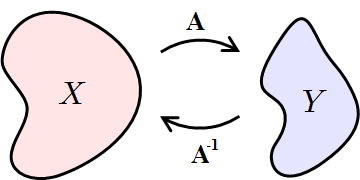
어떤 행렬 $\mathbf{A}$의 역행렬은 $\mathbf{A^{-1}}$로 표현되며, 해당 연산을 되돌리는 개념으로 이해할 수 있다.
$\mathbf{A}\mathbf{A^{-1}} = \mathbf{A^{-1}}\mathbf{A} = \mathbf{I}$ (단, $\mathbf{I}$는 항등행렬)
역행렬이 존재하려면 다음과 같은 조건을 만족해야 한다.
- 행과 열의 개수가 같아야 한다. (즉, 정방행렬이어야 한다.)
- $\det A$가 0이 아니다.
수학적으로 역행렬은 가우스 소거법, 여인자 전개 등의 방법을 사용하여 구할 수 있다. numpy에서는 np.inv를 통해 역행렬을 구할 수 있다.
유사역행렬(pseudo-inverse)
연립방적식과 유사역행렬
정방행렬이 아니어서 역행렬을 구할 수 없으면 유사역행렬 또는 무어 펜로즈(Moore-Penrose) 역행렬 $A^+$를 이용한다.
행이 열보다 수가 많은지 적은지에 따라 유사역행렬의 계산 방법이 달라진다.
$n > m$이고 모든 열벡터가 선형 독립이면, $A+ = (A^TA)^{-1}A^T$
$n \leq m$이고 모든 행벡터가 선형 독립이면, $A+ = A^T(AA^T)^{-1}$
유사역행렬을 통해 $i\leq j$인 경우, 다시 말해서 식이 변수의 개수보다 작거나 같은 경우, $(a_{ij})$와 $(b_{i})$가 주어진 상황에서 이를 만족하는 $(x_j)$를 구하는 문제를 풀 수 있다.
$\mathbf{Ax} = \mathbf{b}$에서 $\mathbf{x}$는 $\mathbf{A}$의 유사역행렬과 $\mathbf{b}$의 곱이 된다.
numpy에서는 np.linalg.pinv()로 유사역행렬을 구할 수 있다.
선형회귀분석과 무어 펜로즈 역행렬
$i \ge j$인 경우는 곧 데이터가 변수보다 많은 경우를 의미하는데, 이때는 무어 펜로즈 역행렬을 선형회귀분석에서 선형회귀식을 찾는 데 사용할 수 있다.
$\mathbf{X}\beta = \hat{\mathbf{y}} \approx \mathbf{y}$
여기서 $\mathbf{X}$는 선형회귀식의 변수, $\beta$는 계수, $\mathbf{y}$는 실제값을 의미한다.
$\mathbf{X}\beta$를 구하면 선형회귀식을 통해 구한 예측값이 되는 것이고, 이를 실제값인 $\mathbf{y}$에 근접하도록 해야 한다.
즉, 예측값에 최대한 근접하도록 지나가는 선형회귀식의 계수를 잘 찾는 것이 관건이다.
그러나 이를 완벽히 만족하는 해를 찾을 수는 없으므로 $\mathbf{\hat{y}}$과 $\mathbf{y}$오차가 최소한이 되는 $\beta$를 찾는다.
이때, Moore-Penrose 역행렬을 이용하면 다음과 같이 정리할 수 있다.
$\beta = \mathbf{(X^{T}X)^{-1}X^T}\mathbf{y}$
정리하면, $\hat{\mathbf{y}}$과 $\mathbf{y}$와의 $L_2$ Norm 거리가 최소일 때의 선형 회귀식이 가장 좋다고 볼 수 있는데, 이 때 최대한 이를 만족하는 계수를 구하는 과정에서 유사 역행렬을 사용한다.
$L_2$ Norm을 가장 최소화하는 선형 모델을 찾을 때 Moore-Penrose 역행렬을 이용하여 선형회귀식의 계수를 구한다.
Positive Definite
먼저 Inner product에 관한 내용은 아래 글에서 자세히 다룬 바 있다.
벡터(Vector)의 정의와 Inner Product(내적) 정리
AI에서 주로 사용하는 기본적인 자료구조인 vector에 관해 알아보고, vector를 이해하는 데 필요한 norm, inner product, orthogonal 등 여러 개념을 살펴보고자 한다. 벡터(Vector)의 정의 벡터는 다음과 같이
glanceyes.com
Symmetric, Positive Definite
Symmteric 하면서 positive definite한 matrix는 ML(Machine Learning)에서 매우 중요한 역할을 하는데, 이들도 inner product로 정의될 수 있다.
$n$차원의 vector space에서 정의되는 inner product $\langle \cdot, \cdot \rangle$와 이 벡터 공간에서의 basis $B = (b_1, \dots , b_n)$가 있다고 가정하자. 그러면 vector space V에 있는 임의의 벡터 $x, y \in V$는 다음과 같이 표현될 수 있다.
$$\begin{align} x = \sum_{i = 1}^n \psi_i b_i \\ y = \sum_{j = 1}^n \lambda_j b_j \end{align}$$
이는 basis의 정의에 의해 vector space의 basis는 그 원소들의 선형결합으로 vector space 내의 존재하는 모든 vector를 나타낼 수 있어서다.
그러면 이 $x, y$의 inner product를 구해보면 다음과 같이 정리할 수 있다.
$$\langle x ,y \rangle = \langle \sum_{i=1}^n \psi_i b_i, \sum_{j=1}^n \lambda_j b_j \rangle = \sum_{i = 1}^n \sum_{j = 1}^n \psi_i \langle b_i, b_j \rangle \lambda_j = \hat{x}^{\intercal} A \hat{y}$$
여기서 행렬 $A$의 각 원소는 basis를 구성하는 요소들의 쌍을 inner product한 것이며, inner product는 정의에 의해 symmetric 하므로 $A$는 자연스럽게 symmetric 하다. 그리고 $\hat{x}$와 $\hat{y}$는 basis $B$에 대한 벡터 $x, y$의 좌표로 해석할 수 있다.
중요한 점은 inner product $\langle \cdot, \cdot \rangle$이 행렬 $A$에 의해 unique 하게 정의된다는 사실이다. 더욱이 inner product는 정의에 의해 positive definite한 성질을 갖고 있으므로 vector space $V$에 관해 영벡터를 제외한 모든 벡터에 관해 다음과 같은 사실을 유추할 수 있다.
$$\forall x \in V \setminus {0} : x^{\intercal} Ax > 0$$
즉, 자기 자신의 벡터에 관한 inner product는 영벡터가 아닌 이상 무조건 0보다 클 수 밖에 없는데, 위의 식을 만족할 때의 $A$를 symmetric, positive definite(또는 그냥 positive definite)이라고 한다. 다시 말해, 위의 식이 바로 행렬 $A$가 symmetric, positive definite 하다는 것의 정의이다.
이것을 직관적으로 이해해 보자면, vector $x$가 존재하고 어떠한 symmetric, positive definite한 matrix $A$로 표현되는 transformation을 $x$에 적용하여 transform 시키면, 그 결과를 $x$와 내적했을 때 0보다 큰 값이 나온다는 것이다. 즉, $x$에서 $A$를 가지고 transformation한 결과의 벡터는 $x$를 기준으로 90도 이내의 비슷한 방향을 가리킨다는 것이다. 만약 0보다 작으면 내적 시 음수가 될 테니까 말이다.
만약 위의 정의에서 $ \gt $ 대신 $ \ge $로 바꾸면 이는 symmteric, semidefinite의 정의이다.
Positive Definite과 Inner Product
만약 행렬 $A$가 vector space인 $\mathbb{R}^{n \times n}$ symmetric positive definite이면, $\hat{x}^{\intercal} A \hat{y}^{\intercal}$은 어떠한 vector space $V$에 속하는 임의의 벡터 $x$, $y$에 대하여 그 vector space를 이루는 어떤 basis $B$에 관해 inner product $\langle x, y \rangle$로 정의될 수 있다.
즉, inner product는 이 $A$에 의해 unique 하게 결정된다는 사실을 유추할 수 있다. 이는 앞서 살펴 본 내용에서도 찾아볼 수 있다.
Positive Definite의 성질
만약 $A \in \mathbb{R}^{n \times n}$가 symmetric, positive definite이면, 다음과 같은 property를 만족한다.
(1) $A$의 null space(kernel)은 영벡터만을 원소로 갖는다. 그 이유는 $x \ne 0$인 모든 벡터 $x$에 관해 $x^{\intercal} A x > 0$를 만족해서다. 이는 $x \ne 0$이면 $Ax \ne 0$임을 내포한다.
(2) $A$의 대각원소인 $a_{ii}$는 모두 positive이다. (0보다 크다.) 이는 $\hat{x}^{\intercal} A \hat{x}^{\intercal}$에서 $x$ 대신 $\mathbb{R}^n$의 standard basis인 $e_i$로 대체하면 $a_{ii} = \hat{e_i}^{\intercal} A \hat{e_i}^{\intercal}$이어서다.
이를 통해 자연스럽게 positive definite matrix의 eigenvalue는 모두 0보다 크다는 사실을 얻을 수 있는데, 이러한 성질을 사용한 예시는 아래 글에서 Fourier features를 다루면서 알아본 적이 있다.
Neural Tangent Kernel과 Fourier Features를 사용한 Positional Encoding (3) - Fourier Features
이 글 시리즈는 'Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains' 논문과 이를 이해하는 데 필요한 선수 내용을 소개한 'Neural Tangent Kernel: Convergence and Generalization in Neural Networks'
glanceyes.com
출처
1. 네이버 부스트캠프 AI Tech Stage 1 기초 수학 강의
2. Mathematics for Machine Learning, Cambridge University Press, Marc Peter Deisenroth
'AI > AI 수학' 카테고리의 다른 글
| [빠르게 정리하는 통계] 머신러닝에서 기본으로 알아야 할 확률분포 개념 (0) | 2023.06.24 |
|---|---|
| [빠르게 정리하는 통계] 자주 쓰이는 확률분포 정리 (0) | 2023.06.23 |
| [빠르게 정리하는 선형대수] 벡터(Vector)의 정의와 Inner Product(내적) 정리 (0) | 2023.03.25 |
| [빠르게 정리하는 선형대수] Eigenvalue와 Eigenvector (0) | 2023.02.21 |
| [인공지능 기초] Uncertainty(2) - 결합 확률과 조건부 확률 그리고 베이즈 정리 (0) | 2023.01.21 |
소중한 공감 감사합니다.