신경망(Neural Network)
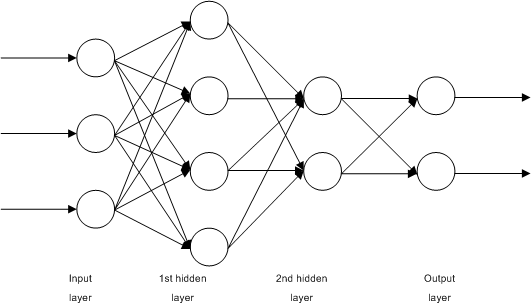
[출처] https://commons.wikimedia.org/wiki/File:Multilayer_Neural_Network.png, John Salatas
선형모델은 단순 데이터를 해석하는데 유용하지만 복잡한 패턴에는 적합하지 않은데, 이러한 복잡한 패턴을 근사할 수 있는 비선형적인 함수가 필요하다.
신경망은 여러 계층의 선형 모델과 비선형성을 부여하는 활성함수(activation function)을 혼합한 합성함수이다.
Feed Forward
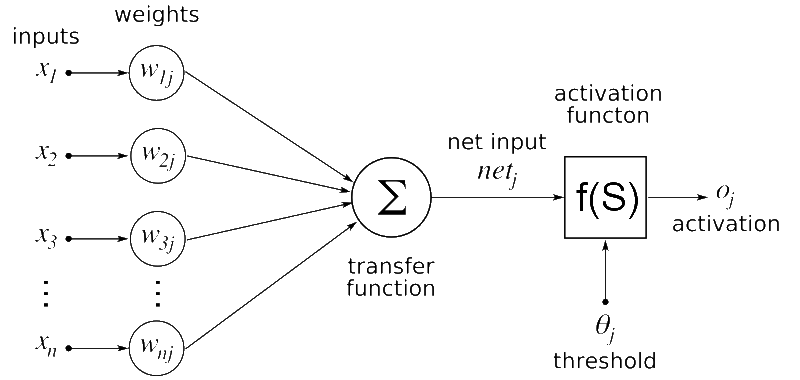
[출처] https://commons.wikimedia.org/wiki/File:Artificial_neural_network.png, Geetika saini
신경망에 입력되는 input 데이터가 존재한다.
- Input Data는 행렬 $\mathbf{X}$로 표현된다.
- 행렬 $\mathbf{X}$의 요소는 벡터인 $\mathbf{x}$로 표현되며, 이 벡터는 $n$개 존재한다.
- 벡터 $\mathbf{x}$내에는 변수 $x_i$가 $d$개 존재할 것이다.
- 즉, Input Data는 $\mathbf{X}(n∗d)$로 표현할 수 있다.
input 데이터를 새로운 차원으로 보내는 가중치 행렬 $\mathbf{W}$도 존재한다.
- $\mathbf{W}$는 Input Data와 내적하기 위해 $d$개의 Vector를 갖는다.
- 이 Vector는 변환하고자 하는 특정 $p$차원을 갖는다.
- 즉, 가중치 행렬은 $\mathbf{W}(d*p)$로 표현된다.
가중치를 내적한 행렬에 덧셈 연산을 하기 위한 절편 $\mathbf{b}$도 존재한다.
- $\mathbf{b}$는 $n$개의 Vector에 대해 적용되기 위해 $n$개의 Vector를 갖는다.
- 이 Vector는 변환하고자 하는 특정 $p$차원을 갖는다.
- 즉, 절편 행렬은 $\mathbf{b}(n*p)$로 표현될 수 있다.
- 이때, 각 열벡터는 동일한 값을 가져 편향의 역할을 한다.
$O = XW + b$의 선형변환을 통해 input 데이터를 새로운 행렬 $\mathbf{O}$로 변환한다.
- 이 행렬의 의미는 $p$ 차원인 벡터 $\mathbf{o}$가 $n$개 존재하는 형태가 된다.
- 즉, 가중치 행렬 $\mathbf{W}(d*p)$과 절편 $\mathbf{b}(n*p)$를 통해 $d$차원의 데이터 벡터 $\mathbf{x}$가 $p$차원의 데이터 벡터 $\mathbf{o}$로 되는 것이다.
- 수학적으로는 $d$개의 변수로 $p$개의 선형모델을 만들어 $n$개의 잠재변수를 만드는 것이다.
선형변환된 데이터 벡터 $\mathbf{o}$에 비선형함수를 적용시켜 비선형적 합성함수를 만들 수 있다.
활성함수(Activation Function)
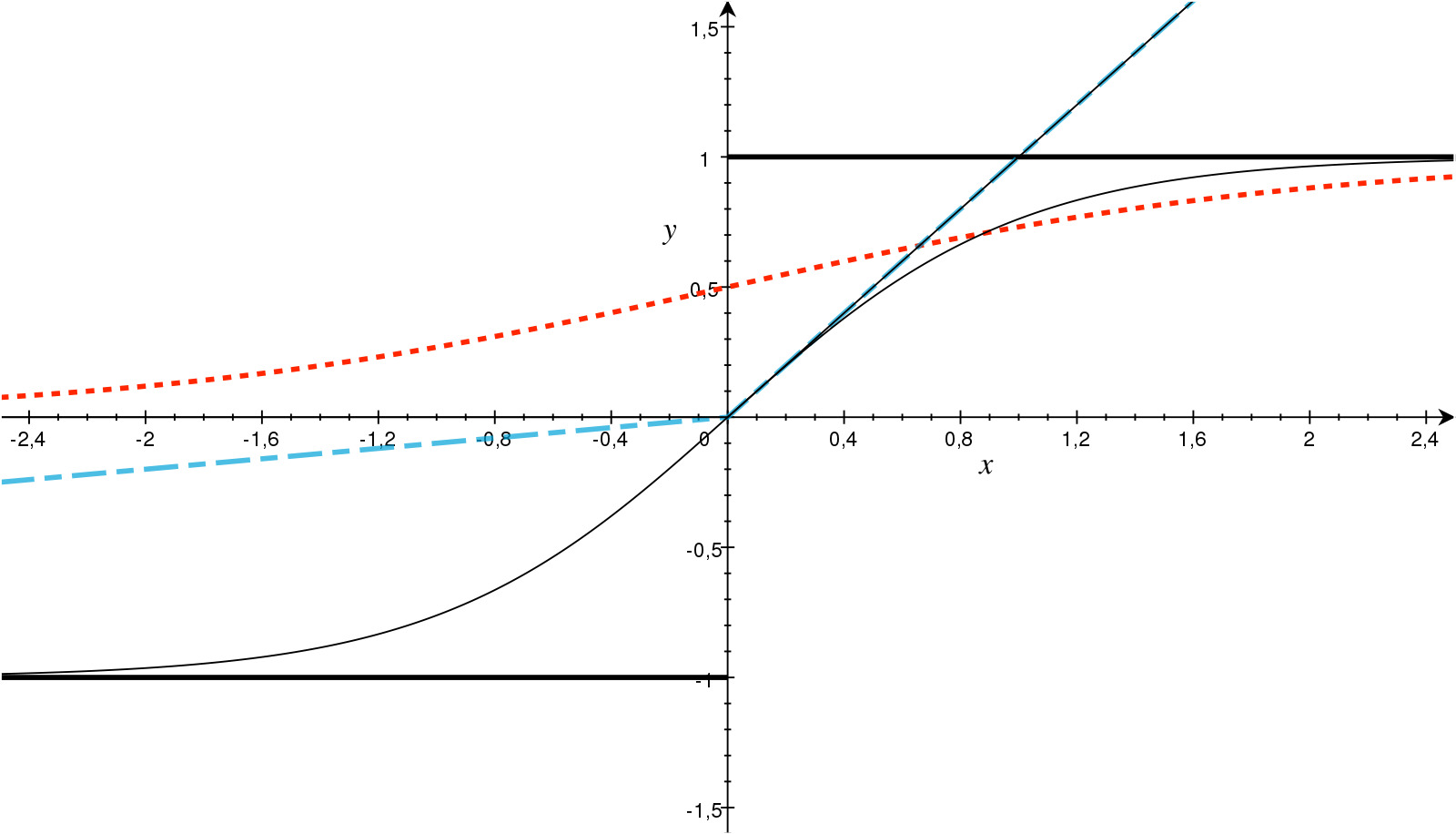
[출처]https://www.sciencedirect.com/science/article/pii/S093938891830120X#fig0010, AKMaier
활성함수는 선형 모델에 비선형성을 부여하기 위한 것으로, 임의의 실수값을 입력받아서 실수값을 출력하는 비선형함수를 의미한다.
활성함수를 사용하지 않는다면 아무리 층이 넓고 깊더라도 선형모델에 불과하게 된다.
그래서 복잡한 패턴과 현상을 파악하기 위해 함수의 비선형적 근사가 필수적이며, 이처럼 비선형적인 변환을 통해 다양한 정보를 포함할 수 있도록 한다.
다양한 활성함수를 적용하여 비선형적인 새로운 잠재벡터의 행렬 $H$를 생성하고 활용할 수 있다.
결국 신경망은 선형모델과 활성함수를 합성한 함수이다.
Softmax (소프트맥스)
softmax는 확률벡터를 출력하는 함수이며, 주로 데이터가 어떠한 분류에 속할 확률이 가장 높은지를 분류하는 예측 모델을 만들 때 사용할 수 있다. 즉, 특정 클래스에 속할 확률 값을 구하는 것이다.
$\text{softmax}(\mathbf{o})$의 $j$번째 원소는 특정 클래스 $j$에 속할 확률 값이 된다.
$$ \text{softmax}(\mathbf{o}) = \bigg(\frac{e^{o_1}}{\sum_{k=1}^p e^{o_k}}, \cdots, \frac{e^{o_p}}{\sum_{k=1}^p e^{o_k}} \bigg) $$
import numpy as np
def softmax(vec) :
denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
numerator = np.sum(denumerator, axis=-1, keepdims=True)
val = denumerator / numerator
return val
vec = np.array(
[[1, 2, 0],
[-1, 0, 1],
[-10, 0, 10]])
softmax(vec)
'''
output
array([[2.44728471e-01, 6.65240956e-01, 9.00305732e-02],
[9.00305732e-02, 2.44728471e-01, 6.65240956e-01],
[2.06106005e-09, 4.53978686e-05, 9.99954600e-01]])
'''
이 외에도 전통적으로 사용하는 sigmoid, tanh, 그리고 근래에 자주 사용하는 ReLU 등 다양한 활성함수가 있다.
ReLU를 딥러닝에서 활성함수로 상대적으로 많이 사용하는 이유
ReLU(Rectified Linear Unit) 함수 그래프
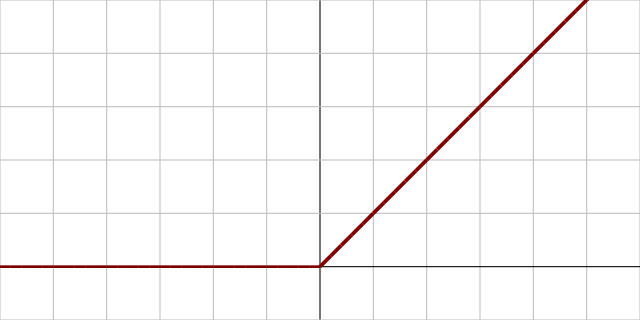
[출처] https://commons.wikimedia.org/wiki/File:Activation_rectified_linear.svg, Laughsinthestocks
시그모이드(sigmoid) 함수 그래프
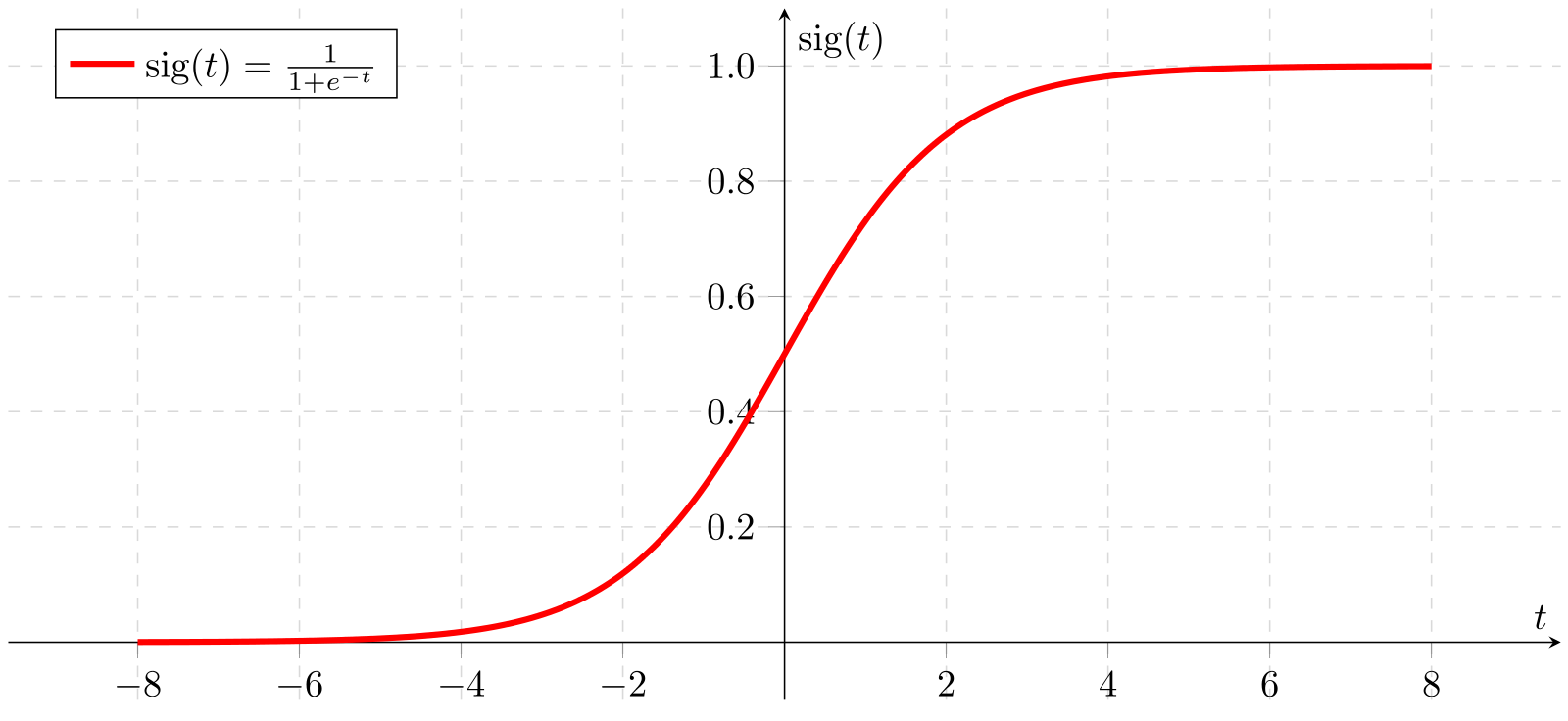
시그모이드(sigmoid) 함수는 항상 0과 1 사이, tanh 함수는 함숫값이 항상 -1보다 크거나 1보다 작을 뿐만이 아니라 입력의 절댓값이 크면 클수록 미분 값이 0에 가까워지는 특징이 있어서 역전파(Backpropagation) 알고리즘에서 Chain Rule을 적용하여 gradient vector를 구할 때 이 값이 0에 가까워지는 기울기 소멸 문제(Vanishing Gradient Problem)이 발생한다.
특히 여러 계층의 신경망에서 역전파 알고리즘을 사용하면 앞쪽 계층에 위치한 gradient vector를 구할 때 뒤에서부터 Chain Rule에 의해 여러 gradient 값이 곱해지므로 0에 빠르게 수렴한다.
Layers
전통적인 Perceptron은 input data를 선형변환한 후, 활성함수를 통해 출력한다.
출력된 Output data를 다시 새로운 층의 Input data로 사용하면, Perceptron이 여러 층처럼 구성되는데, 이러한 형태를 Multi Layer Perceptron이라 한다.
신경망을 이렇게 여러 층으로 구성하는 이유는 넓은 형태의 신경망이 비효율적이기 때문이다.
얕고 넓게 신경망을 구축하면 목적함수에 근사하기 위해 필요한 노드의 수가 기하급수적으로 늘어니는데, 실제로 이러한 신경망은 잘 작동하지 않는다.
층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 수가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능하지만, 층이 너무 깊으면 최적화가 어려워서 오히려 학습이 불가능해질 수도 있다.
그래서 적절한 수준으로 신경망을 구축해야 한다.
Backpropagation (역전파 알고리즘)
최종적으로 출력된 Output과 손실함수를 통해 모델의 파라미터(가중치, 절편 등)를 최적화할 수 있다.
즉, 손실함수의 값을 줄이기 위해 파라미터를 최적화하는 작업(학습)을 해야하며, 이를 위해 역전파 알고리즘이 사용된다.
경사하강법을 적용하여 각 perceptron의 가중치와 절편를 업데이트 해야하며, 선형모델에서 $β$의 gradient vector $∇_β$를 구한 것처럼 각 층에 존재하는 가중치와 절편의 미분값을 구해야 한다.
미분값은 한번에 계산되지 않고, chain rule에 의해 상위층부터 하위층으로 순차적으로 계산되어 내려온다.
근래의 Deep Learning Framework에서는 자동미분을 사용하는데, 각 뉴런이 전달받은 값의 형태와 출력 값을 기억하여 Gradient를 구하는 것이다.
각 뉴런은 해당 값을 메모리에 저장해놓아야 하기 때문에 역전파 알고리즘은 순전파에 비해 메모리를 상대적으로 더 많이 요구한다.
이미 Framework에 구현되어 있는 자동미분 역전파 알고리즘(예: pytorch의 autograd())에 의해 현재는 신경망을 구현하여 학습시키면 주어진 목적식을 최소화하는 파라미터를 구할 수 있다.
출처
1. 네이버 부스트캠프 AI Tech Stage1 수학 기초 강의