2022년 1월 17일(월)부터 21일(금)까지 네이버 부스트캠프(boostcamp) AI Tech 강의를 들으면서 개인적으로 중요하다고 생각되거나 짚고 넘어가야 할 핵심 내용들만 간단하게 메모한 내용입니다. 틀리거나 설명이 부족한 내용이 있을 수 있으며, 이는 학습을 진행하면서 꾸준히 내용을 수정하거나 추가해나갈 예정입니다.
CNN(Convolutional Neural Network)
CNN이란?
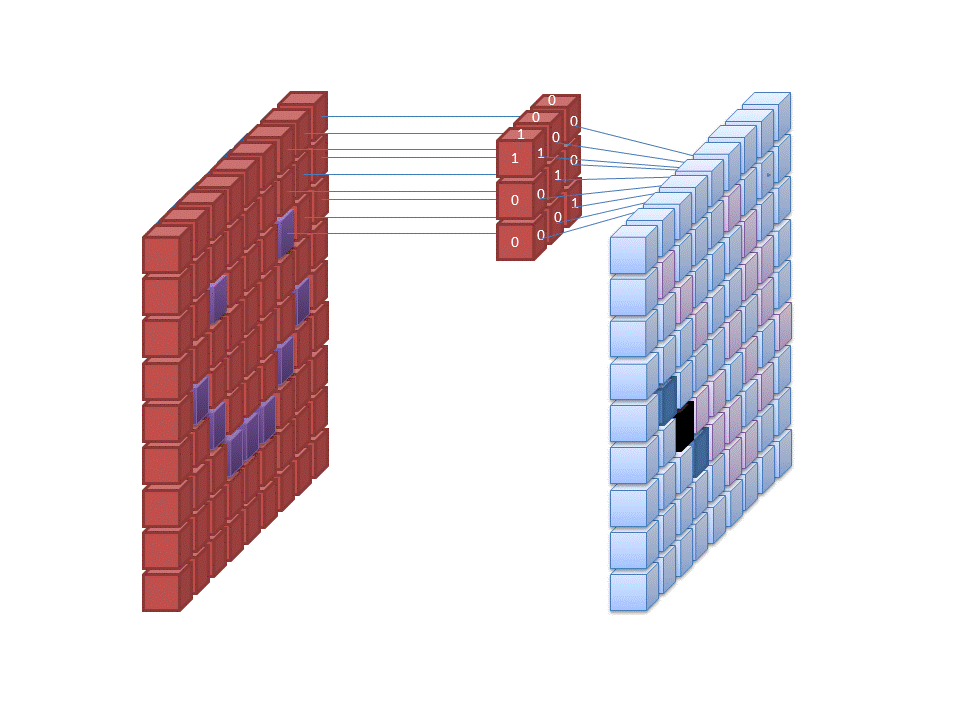
[출처] https://commons.wikimedia.org/wiki/File:Convolutional_Neural_Network_NeuralNetworkFilter.gif, Cecbur
다층신경망(MLP)에는 각 뉴런들이 선형 모델과 활성 함수로 모두 연결된 구조도 존재하지만, 커널(kernel)이란 것을 사용하여 입력 벡터 상에서 이를 움직여 가면서 convolution 연산을 진행하는 선형 모델과 합성함수가 적용되는 구조도 존재하는데, 이를 CNN이라고 한다.
CNN은 딥러닝의 한 종류로서 주로 이미지 등을 분석하는 데 사용하며, 커널(Kernel)이라는 것을 활용한다.
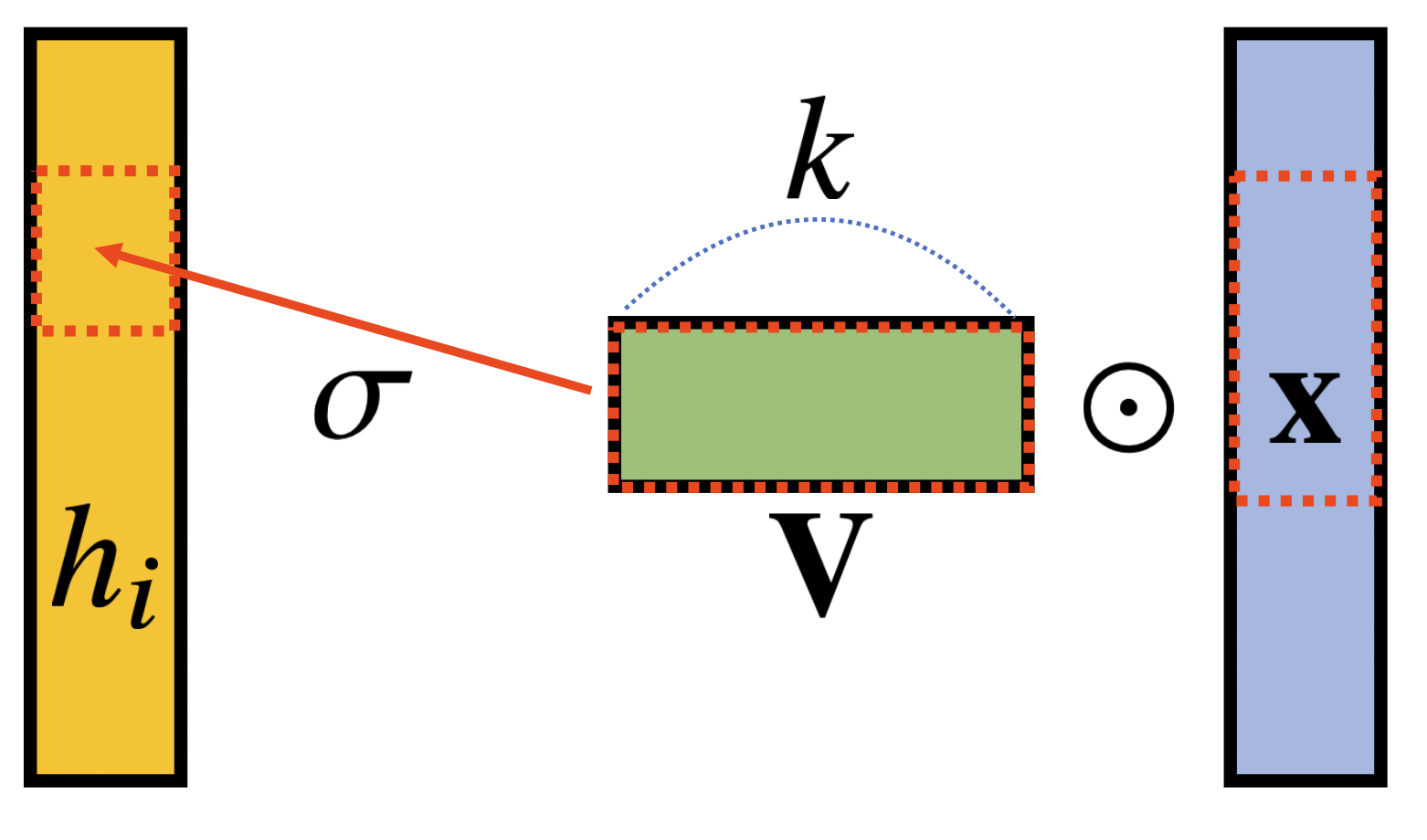
Convolution 연산
$$ [f*g](x) = \int_{\mathbb{R}^d}f(z)g(x-z)dz = \int_{\mathbb{R}^d} f(x-z)g(z)dz = [g*f](x) $$
$$ [f*g](i) = \sum_{a\in \mathbb{Z}^d} f(a)g(i-a) = \sum_{a\in \mathbb{Z}^d} f(i-a)g(a) = [g*a](i) $$
두 개의 함수 $f$, $g$가 있을 때, $x$라는 입력 신호에 관해 전체 정의역에서 $z$를 움직여가며 두 함수 $f$, $g$를 곱한 것을 적분해주는 형태이다.
Convolution 연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것이다.
CNN 에서 사용하는 연산은 사실 convolution이 아니고 cross-correlation이지만, 관용적으로 CNN에서는 convolution 연산을 사용한다고 말한다.
convolution 연산을 미분해도 convolution 연산이 나오는 특징이 있으며, Discrete일 때도 마찬가지로 성립한다.
커널은 정의역 내에서 움직여도 그 형태나 크기 등은 변하지 않고, 커널을 통해 처리하는 결과는 주어진 신호에 국소적으로 영향을 받는다.
2차원에서의 Convolution 연산
$$ [f*g](i,j) = \sum_{p,q} f(p,q)g(i+p, j+q) $$
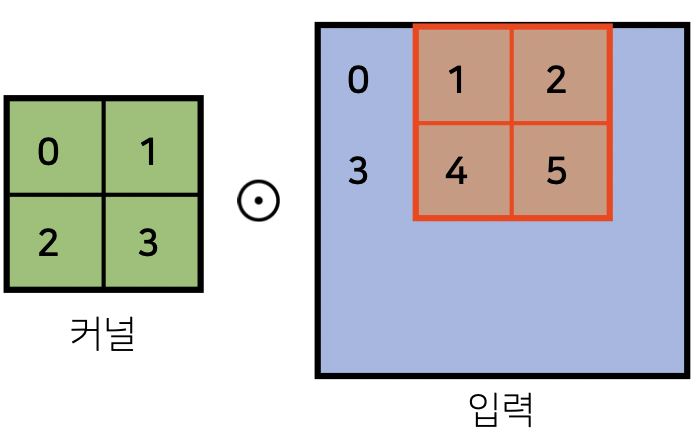
CNN에서 출력 데이터의 크기 구하기
커널 크기: $(K_H, K_W)$
입력 데이터 크기: $(H, W)$
출력 크기: $(H - K_H + 1) * (W - K_W + 1)$
채널(Channel)과 Convolution 연산
입력의 채널이 여러 개일 때는 채널에 관해 convolution을 적용한다.
채널 수: $C$
커널 수: $K$
커널 크기: $(K_H, K_W, C)$
입력 데이터 크기: $(H, W, C)$
출력 크기: $(H - K_H + 1) * (W - K_W + 1) * K$
CNN에서의 역전파 알고리즘
$$ \begin{align} \frac{\partial}{\partial{x}} [f*g](x) &= \frac{\partial}{\partial{x}} \int_{\mathbb{R}^d} f(y)g(x-y)dy\\ &= \int_{\mathbb{R}^d} f(y) \frac{\partial}{\partial{x}}g(x-y)dy \\ &= [f*g'](x) \end{align} $$
Convolution 연산은 커널의 모든 입력데이터에 공통으로 적용되기 때문에 역전파 알고리즘을 사용할 때도 convolution 연산이 나온다.
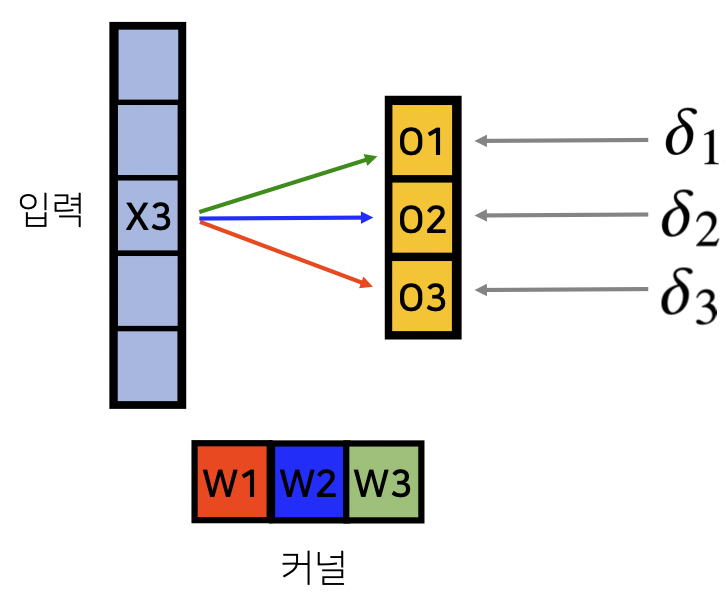
Backpropagation을 수행할 때 $x_3$는 다음과 같이 업데이트 된다.
$x_1 = \partial_1 w_1$
$x_2 = \partial_1 w_2 + \partial_2 w_1$
$x_3 = \partial_1 w_3 + \partial_2 w_2 + \partial_3 w_1$
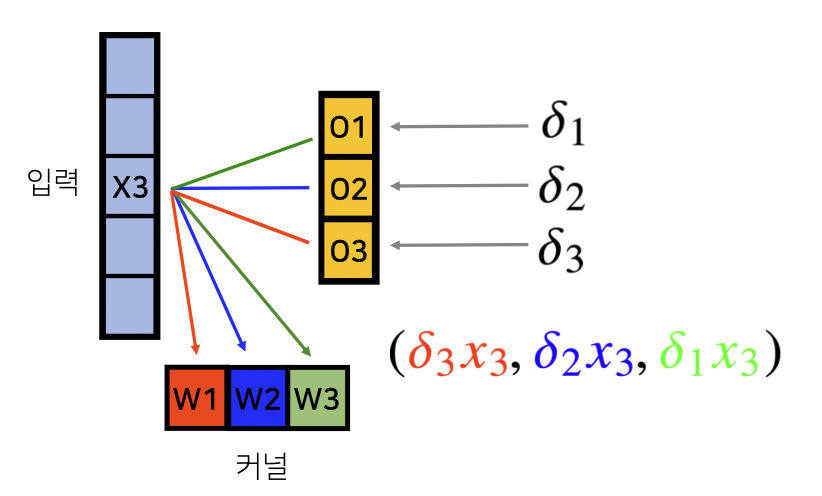
역전파 단계에서 다시 커널로 가중치의 gradient가 전달된다.
$ (w_1, w_2, w_3) \leftarrow (\partial_3 x_3, \partial_2 x_3, \partial_1x_3)$
정리하면, $\frac{\partial{\mathcal{L}}}{\partial w_1} = \partial_1 x_1 + \partial_2 x_2 + \partial_3 x_3$로 커널의 가중치 $w_1$이 업데이트 된다.