Deep Learning 기반의 Collaborative Filtering
- -
Deep Learning-based Collaborative Filtering
추천 시스템에서 Deep Learning 모델의 장점
Non-Linear Transformation
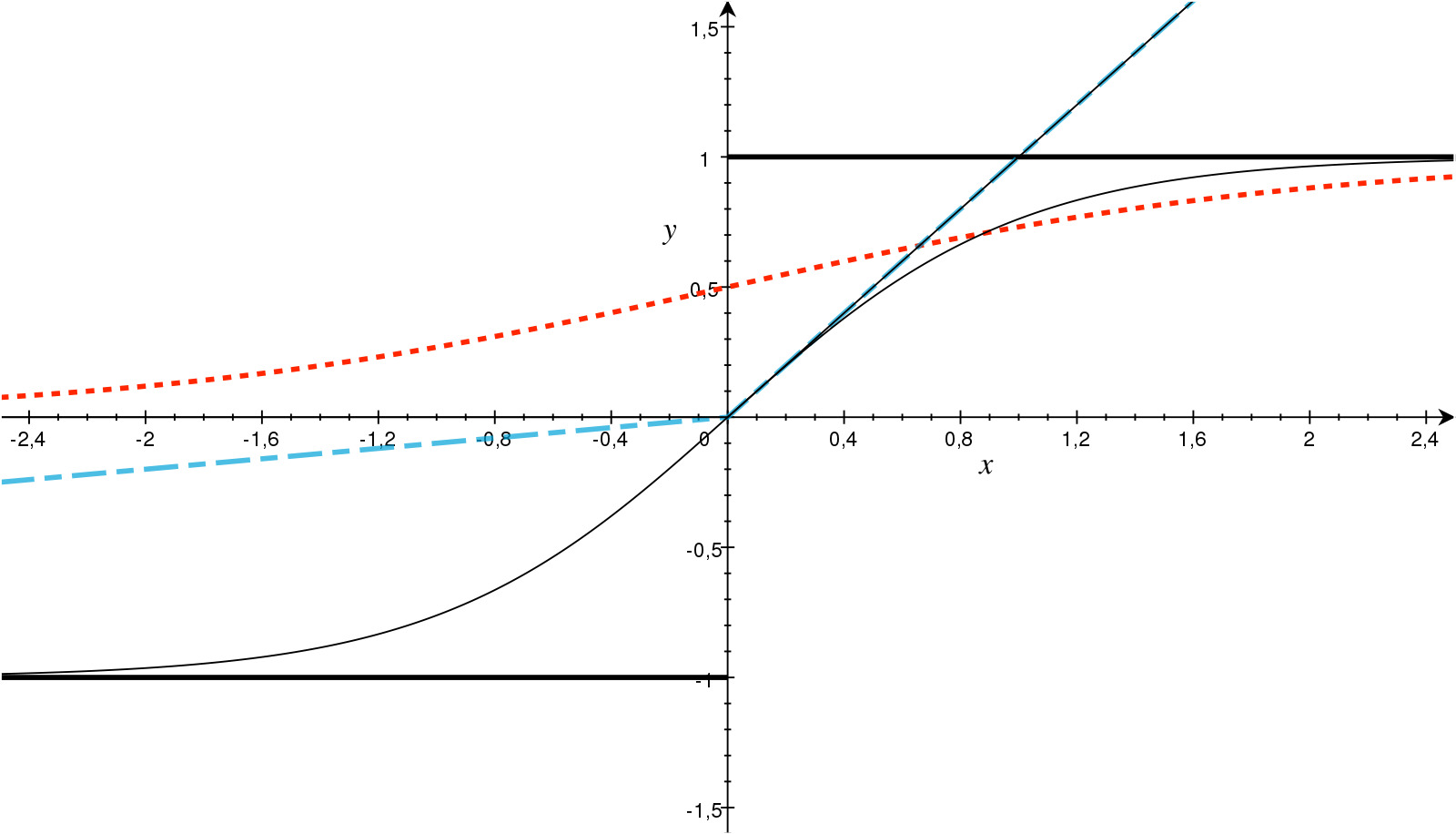
[출처] https://www.sciencedirect.com/science/article/pii/S093938891830120X#fig0010, AKMaier
ReLU, Sigmoid, Tanh와 같은 비선형 활성화함수를 활용해 복잡한 사용자-아이템 간 상호작용을 포착할 수 있다.
Representation Learning
Feature-engineering에 드는 수고를 덜어주며, 여러 다른 종류들로 이루어진 다차원적인 콘텐츠 정보를 포함할 수 있다.
즉, 이미지, 비디오 등 Multi-Modality의 특성을 지닐 수 있다.
Sequence Modeling
RNN, Transformer 모델을 활용해 순차적인 사용자의 액션에 알맞은 추천을 할 수 있다.
Flexibility
다양한 네트워크 구조를 쉽게 결합할 수 있으며, TensorFlow, PyTorch 등 여러 딥 러닝 프레임워크 오픈 소스가 존재한다.
추천 시스템에서 Deep Learning 모델의 한계
Interpretability
Neural Network의 구성 요소들의 Interpretability는 블랙박스에 가까워서 여전히 중요한 연구 주제이며, 이를 고려한 새로운 연구들이 지속적으로 나오고 있다.
Data Requirement
전통적인 머신러닝 기법에 비해 유의미한 성능을 내기 위해서는 필요로 하는 데이터의 양이 많다.
그럼에도 불구하고 추천 시스템에서는 NLP 또는 CV 분야에 비하면 다루는 데이터의 크기가 상대적으로 적은 편이다.
Extensive Hyperparameter Tuning
딥 러닝 뿐만이 아니라 머신러닝의 전반적인 문제라고 볼 수 있지만, 딥 러닝에서는 특히 Hyperparameter를 어떻게 튜닝할 것인지가 꽤 중요한 문제가 될 수 있다.
딥 러닝을 통한 CF 모델의 예시
Matrix Factorization에서 사용자와 아이템 간 상호작용 행렬을 유저와 아이템의 잠재 요인 행렬로 각각 분해했는데, 이 잠재 요인을 지닌 행렬을 만드는 임의의 함수 $f$를 deep nueral architecture로 대체한다고 볼 수 있다.
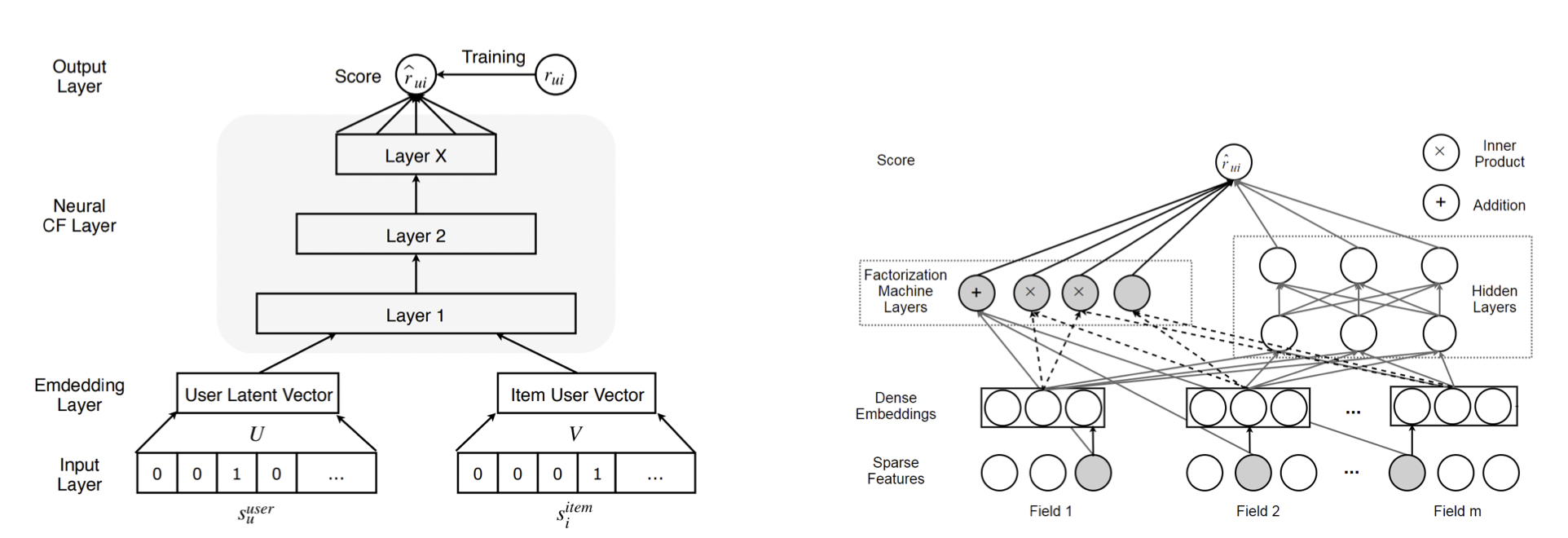
[출처] https://arxiv.org/pdf/1707.07435.pdf, Deep Learning based Recommender System: A Survey and New Perspectives
이에 관한 모델 사례로 NCF(Neural Collaborative Filtering), AutoRec, Deep Matrix Factorization 등이 존재한다.
딥 러닝 모델에 비해 MF가 갖고 있는 한계
Compatibility function을 모델링함에 있어서 MF에서는 사용자 term인 $\gamma_u$와 아이템 term인 $\gamma_i$의 관계를 모델링할 때 inner product를 사용하지만, 딥 러닝 모델에서는 DNN을 사용한다.
이는 MF의 inner product가 가지는 linearity 특성으로 인해 표현력에 한계가 존재하기 때문이다.
Autoencoder 기반의 CF
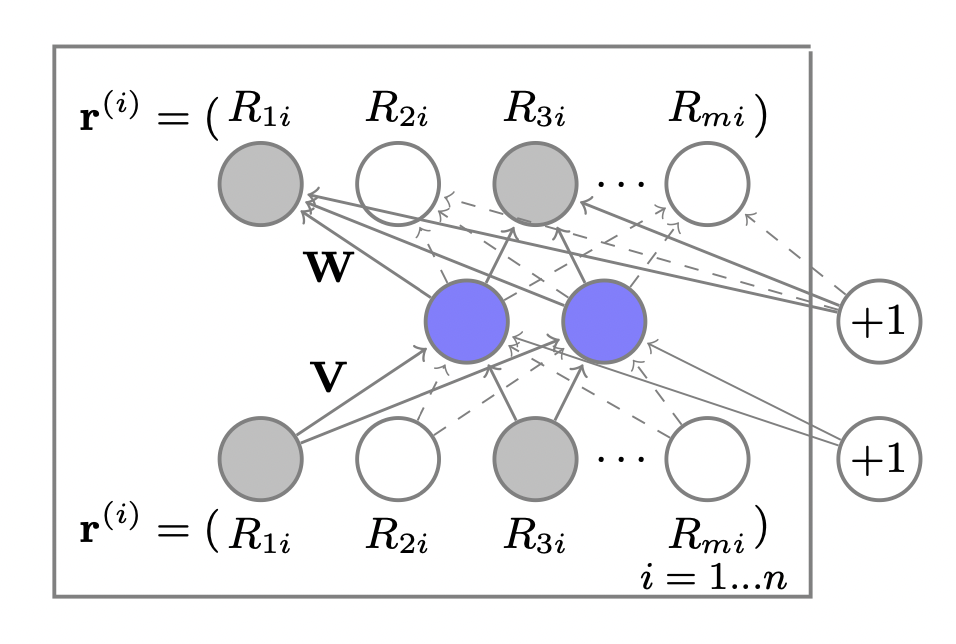
[출처] https://users.cecs.anu.edu.au/~akmenon/papers/autorec/autorec-paper.pdf, AutoRec: Autoencoders Meet Collaborative Filtering
차원 축소 테크닉이자 self-supervised learning(비지도학습) 방법의 하나인 Autoencoder를 추천 시스템의 sparse한 데이터의 상황에 적합하도록 Formulation한 형태이다.
입력값인 rating을 reconstruction(decoding) 할 수 있게끔 학습함으로써 rating이 가지고 있는 잠재적인 패턴이 latent code에 암호화될 수 있도록 하는 방법이다.
평점 예측에서는 rating 값을 reconsturction, 즉 복호화할 수 있도록 학습한다.
Top-K ranking의 경우 상호작용이 발생할 확률을 reconstruction하도록 학습한다.
Training set으로 학습한 후, 학습 과정에서는 나타나지 않았던 testing set에 관해 평가를 진행한다.
예를 들어, 사용자와 아이템 간 상호작용 데이터를 가진 행렬 $R$을 autoencoder로 encoding하면 decoding을 통해 이것이 행렬 $R'$으로 reconstruction 된다.
$R$에 담겨진 모든 정보를 가운데 있는 encoder와 decoder 사이의 latent code가 요약하여 갖고 있게 된다.
이 latent code를 information bottleneck이라고도 하며, latent code는 행렬 $R$을 행렬 $R'$으로 reconstruction 하는 데 중요한 정보를 담고 있다고 볼 수 있다.
알려지지 않은 평점이 0으로 기본적으로 설정되어 있는 평점 행렬인 $R$의 $u$번째 행인 $R_u$가 주어졌을 때, $R_u$를 reconstruction하는 과정과 그에 따른 목적함수는 다음과 같이 정의될 수 있다.
여기서 $f$와 $g$는 비선형 활성함수, $\mathbf{W}$와 $\mathbf{V}$는 가중치 행렬, $\mu$와 $b$는 편향, $\| \cdot \|_{\mathcal{O}}^2$는 관측된 값에 관해서만 고려하겠다는 의미이다.
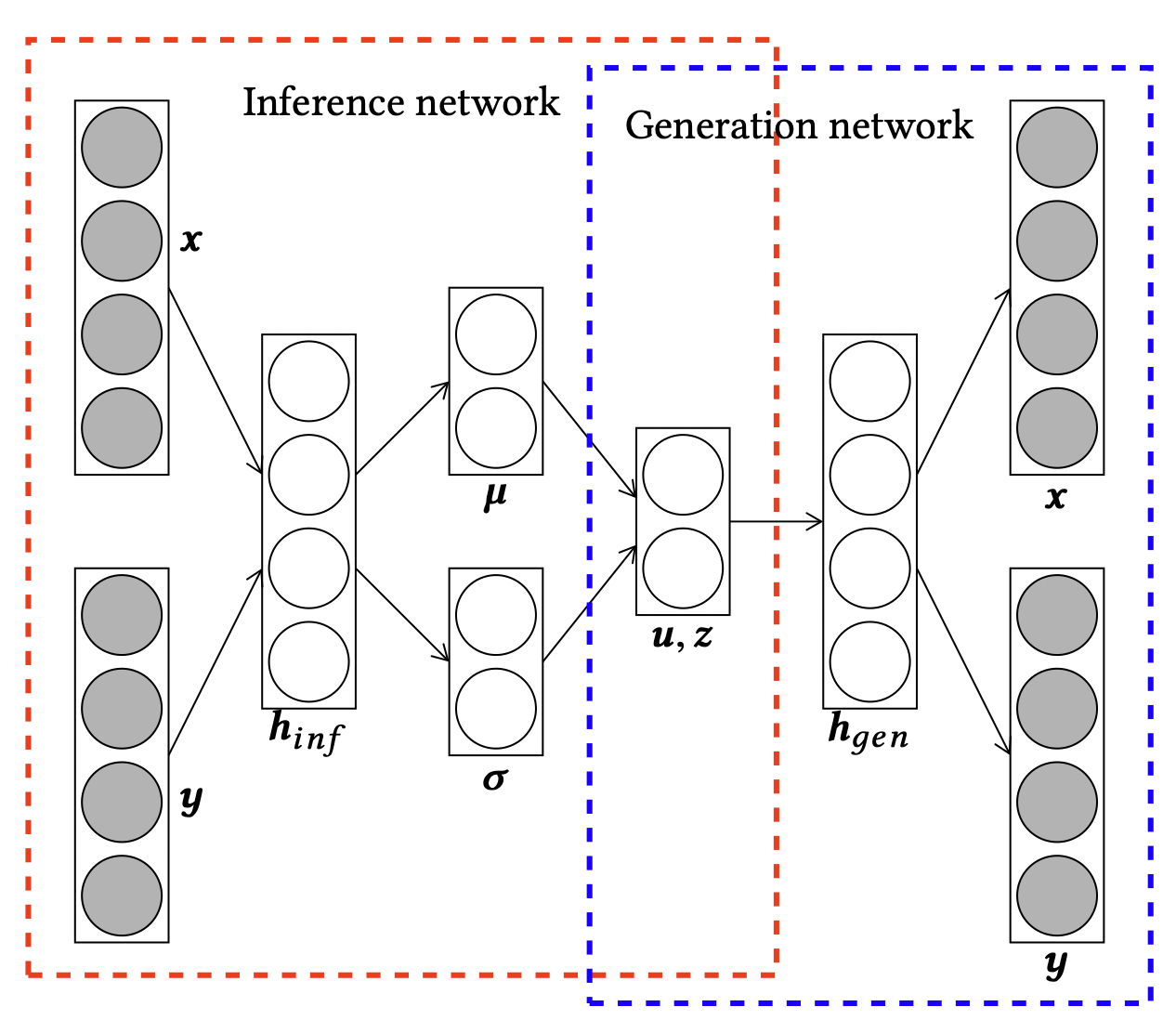
[출처] https://arxiv.org/pdf/1807.05730.pdf, A Collective Variational Autoencoder for Top-N Recommendation with Side Information
Autoencoder 기반 모델에 side information도 같이 고려할 수 있는 방법이 있는데, 이는 input의 앞에 아이템에 대한 임베딩 벡터를 붙여서 encoder layer에 통과시키는 것이다. 이럴 경우 샘플링 분포에서 아이템의 임베딩 벡터를 반영한 모수가 나온다.
Decoder layer의 output으로 나온 재생성된 input에서 임베딩 벡터 부분만 따로 뗄 수 있도록 split하면 된다.
아래 코드는 Multi-DAE를 사용하여 사용자가 본 영화 이력을 바탕으로 새로운 영화를 추천할 때, 영화 아이템의 장르와 타이틀이라는 side-information을 추가하여 모델의 성능을 향상시킨 기법이다.
class MultiDAE(nn.Module):
"""
Container module for Multi-DAE.
Multi-DAE : Denoising Autoencoder with Multinomial Likelihood
See Variational Autoencoders for Collaborative Filtering
https://arxiv.org/abs/1802.05814
"""
def __init__(self, p_dims, q_dims=None, dropout=0.5):
super(MultiDAE, self).__init__()
self.item_genre = torch.Tensor(item_genre_emb.values) ##### 추가
self.item_title = torch.Tensor(item_title_emb.values) ##### 추가
self.p_dims = p_dims
if q_dims:
assert q_dims[0] == p_dims[-1], "In and Out dimensions must equal to each other"
assert q_dims[-1] == p_dims[0], "Latent dimension for p- and q- network mismatches."
self.q_dims = q_dims
else:
self.q_dims = p_dims[::-1]
self.dims = self.q_dims + self.p_dims[1:]
self.layers = nn.ModuleList([nn.Linear(d_in, d_out) for
d_in, d_out in zip(self.dims[:-1], self.dims[1:])])
self.drop = nn.Dropout(dropout)
self.init_weights()
def forward(self, input):
h = F.normalize(input)
h = torch.cat((self.item_genre.to(device), self.item_title.to(device), h), 0) ###추가
h = self.drop(h)
#print('합친 h.shape: ', h.shape)
for i, layer in enumerate(self.layers):
h = layer(h)
if i != len(self.layers) - 1:
h = F.tanh(h) #reluX
reconstructed_genre, reconstructed_title, reconstructed_h = h.split([self.item_genre.shape[0], self.item_title.shape[0], input.shape[0]], 0) ##추가
return reconstructed_genre, reconstructed_title, reconstructed_h
def init_weights(self):
for layer in self.layers:
# Xavier Initialization for weights
size = layer.weight.size()
fan_out = size[0]
fan_in = size[1]
std = np.sqrt(2.0/(fan_in + fan_out))
layer.weight.data.normal_(0.0, std)
# Normal Initialization for Biases
layer.bias.data.normal_(0.0, 0.001)
마찬가지로 Multi-VAE에도 side-information을 추가할 수 있다.
class MultiVAE(nn.Module):
"""
Container module for Multi-VAE.
Multi-VAE : Variational Autoencoder with Multinomial Likelihood
See Variational Autoencoders for Collaborative Filtering
https://arxiv.org/abs/1802.05814
"""
def __init__(self, p_dims, q_dims=None, dropout=0.5):
super(MultiVAE, self).__init__()
self.p_dims = p_dims
self.item_genre = torch.Tensor(item_genre_emb.values) ##### 추가
self.item_title = torch.Tensor(item_title_emb.values) ##### 추가
if q_dims:
assert q_dims[0] == p_dims[-1], "In and Out dimensions must equal to each other"
assert q_dims[-1] == p_dims[0], "Latent dimension for p- and q- network mismatches."
self.q_dims = q_dims
else:
self.q_dims = p_dims[::-1]
# Last dimension of q- network is for mean and variance
temp_q_dims = self.q_dims[:-1] + [self.q_dims[-1] * 2]
self.q_layers = nn.ModuleList([nn.Linear(d_in, d_out) for
d_in, d_out in zip(temp_q_dims[:-1], temp_q_dims[1:])])
self.p_layers = nn.ModuleList([nn.Linear(d_in, d_out) for
d_in, d_out in zip(self.p_dims[:-1], self.p_dims[1:])])
self.h_temp = None
self.drop = nn.Dropout(dropout)
self.init_weights()
def forward(self, input):
self.input = input
mu, logvar = self.encode(input)
z = self.reparameterize(mu, logvar)
recon_gen, recon_tit, recon_batch = self.decode(z)
return recon_gen, recon_tit, recon_batch, mu, logvar
def encode(self, input):
h = F.normalize(input)
h = torch.cat((self.item_genre.to(device), self.item_title.to(device), h), 0) ###추가
h = self.drop(h)
for i, layer in enumerate(self.q_layers):
h = layer(h)
if i != len(self.q_layers) - 1:
h = F.tanh(h)
else:
mu = h[:, :self.q_dims[-1]]
logvar = h[:, self.q_dims[-1]:]
return mu, logvar
def reparameterize(self, mu, logvar):
if self.training:
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return eps.mul(std).add_(mu)
else:
return mu
def decode(self, z):
h = z
for i, layer in enumerate(self.p_layers):
h = layer(h)
if i != len(self.p_layers) - 1:
h = F.tanh(h)
reconstructed_genre, reconstructed_title, reconstructed_h = h.split([self.item_genre.shape[0], self.item_title.shape[0], self.input.shape[0]], 0) ##추가
return reconstructed_genre, reconstructed_title, reconstructed_h
def init_weights(self):
for layer in self.q_layers:
# Xavier Initialization for weights
size = layer.weight.size()
fan_out = size[0]
fan_in = size[1]
std = np.sqrt(2.0/(fan_in + fan_out))
layer.weight.data.normal_(0.0, std)
# Normal Initialization for Biases
layer.bias.data.normal_(0.0, 0.001)
for layer in self.p_layers:
# Xavier Initialization for weights
size = layer.weight.size()
fan_out = size[0]
fan_in = size[1]
std = np.sqrt(2.0/(fan_in + fan_out))
layer.weight.data.normal_(0.0, std)
# Normal Initialization for Biases
layer.bias.data.normal_(0.0, 0.001)
부스트캠프의 Level 2의 Movie Recommendation(영화 추천) 대회를 진행하면서 현재 글을 쓰는 시점 기준으로 가장 성능이 좋게 나오는 모델이 바로 이 auto encoder를 사용한 multi variational encoder와 multi denoising encoder 모델이다.
이 대회에서는 사용자가 평가한 영화 순서가 원본 데이터 그대로 주어지지 않고 순서 중 일부를 제외하는 전처리 과정을 거친 데이터를 사용하는데, 이로 인해 sequential data에 강한 BERT4Rec, SASRec보다 static data에 좀 더 강점을 보이는 auto encoder가 더 좋은 추천 결과를 보이는 게 아닌가 하는 생각이 들었다.
평점 예측을 위한 Deep Learning-based CF
평점 예측과 Explicit Feedback
평점 예측 문제는 real-value로 이뤄진 explicit feedback을 예측하는 태스크에 주로 사용되며, explicit feedback은 아이템의 별점과 같이 사용자의 선호에 관한 명시적인 정보를 제공한다고 볼 수 있다.
U/I(User or Item based)-RBM(Restricted Boltzmann Machines)
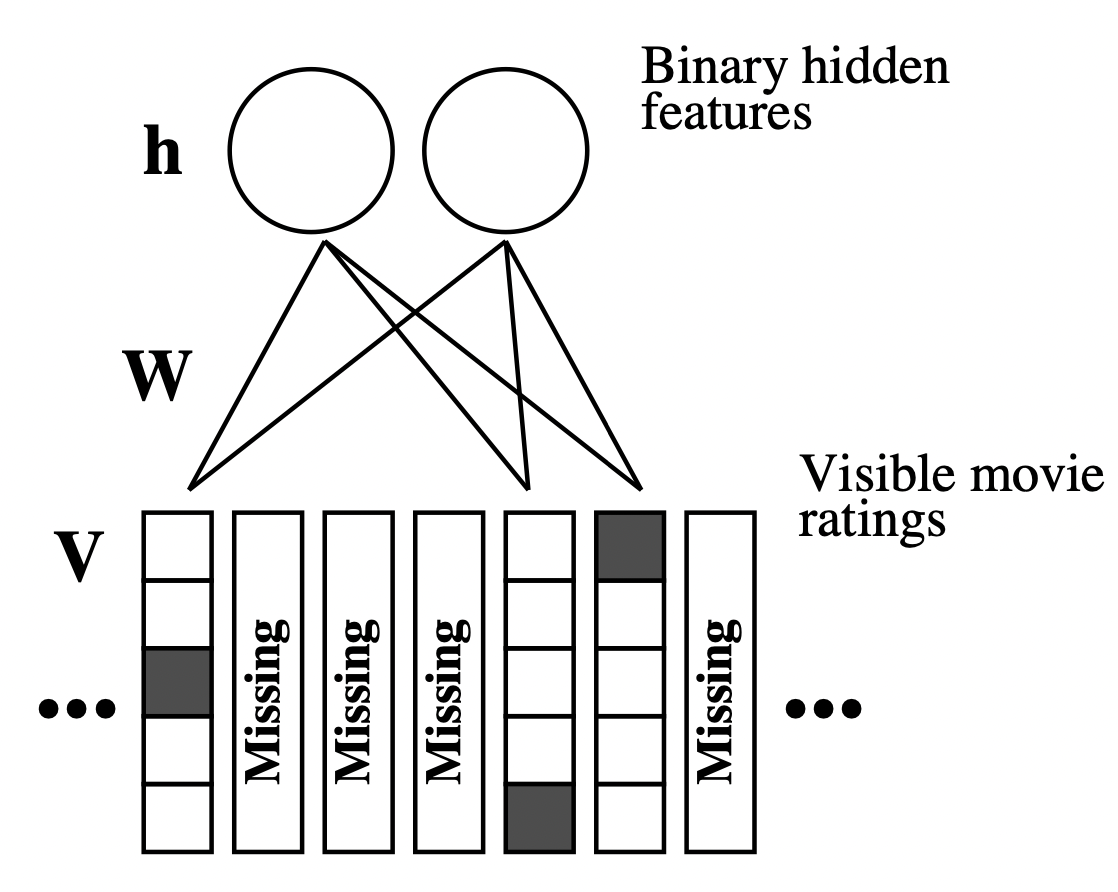
[출처] https://www.cs.toronto.edu/~rsalakhu/papers/rbmcf.pdf, Restricted Boltzmann Machines for Collaborative Filtering
RBM(Restricted Boltzmann Machines)을 활용한 기법으로, 최초로 Neural Net을 활용한 추천 모델 중 하나이다.
여기서 RBM은 대표적인 비지도 방식 중 하나이자 Generative Model의 일종으로, 모든 visible layer의 node와 hidden layer의 node가 bipartite graph(이분 그래프)처럼 연결된 구조를 갖는 모델이다.
'Restricted'라는 명칭이 붙은 이유는 모델이 이분 그래프처럼 같은 layer 내부에서는 연결이 존재하지 않는 형태이기 때문이다.
입력층인 visible layer는 input으로 받은 입력 데이터를 hidden layer에 얼마나 전달할 것인지를 확률에 따라 결정한다.
User-based RBM에서는 user 별 item에 관한 rating을 visible layer에 입력한다.
Item-based RBM에서는 item 별 user에 관한 rating을 visible layer에 입력한다.
여기서는 기본적으로 user-based로 소개되었지만, visible layer의 입력에 따라 변경이 가능하다.
RBM의 경우 1~5점의 평점 예측을 Regression이 아니라 $\{ 1, 2, 3, 4, 5 \}$의 label을 갖는 multi-class classification 문제로 변환할 수 있다.
각 사용자에 관한 visible layer인 $\mathbf{V}$는 $5 \times |I|$의 binary indicator가 된다.
U/I(User or Item based)-AutoRec
가장 기본적인 Autoencoder를 적용한 모델이며, user 또는 item 별 평점을 입력 값을 사용한 후에 출력 값과의 error를 확인한다.
Backpropagation 과정에서 전체 노드에 적용하는 게 아니라 관측된 rating과 관련 있는 노드에 관해서만 업데이트한다는 특징이 있다.
대개 아이템 기반의 Autoencoder 사용자 기반의 Autoencoder보다 더 잘 동작하는 경향을 보이는데, 이는 아이템 별 rating이 유저 별 rating보다 압도적으로 많기 때문이라고 알려져 있다.
Encoder와 Decoder 별 활성화 함수를 어떻게 조합하느냐에 따라 성능 차이가 큰 모습을 보인다.
Hidden Layer의 뉴런 수 또는 레이어 개수를 높이면 더 좋은 성능을 보인다고 한다.
Top-K Ranking을 위한 Deep Learning-based CF
Top-K Ranking과 Implicit Feedback
Top-K Ranking 문제는 0과 1의 binary-value로 이루어진 implicit feedback을 예측하는 태스크에 주로 사용되며, implicit feedback은 사용자의 아이템에 관한 클릭, 구매 등 사용자의 선호에 관해 암시적인 정보만을 제공한다고 볼 수 있다.
NeuMF(Neural Matrix Factorization)
Neural Matrix Factorization = Generalized MF + MLP
Compatibility function으로 element-wise product와 concatenation을 사용했으며, GMF의 입력으로는 사용자와 아이템 벡터를 element-wise product 연산 결과를, MLP의 입력으로는 사용자와 아이템 벡터를 concatenation한 결과를 넣어준다.
MF 모델의 한계로 지적되어 온 linear model의 표현력의 한계를 극복하고자 하는 것이지만, 이후의 연구들에서는 NeuMF가 MF보다 상대적으로 그렇게 성능이 좋지는 않다는 반대되는 결과가 보고되기도 한다.
CDAE(Collaborative Denoising Auto-Encoders)
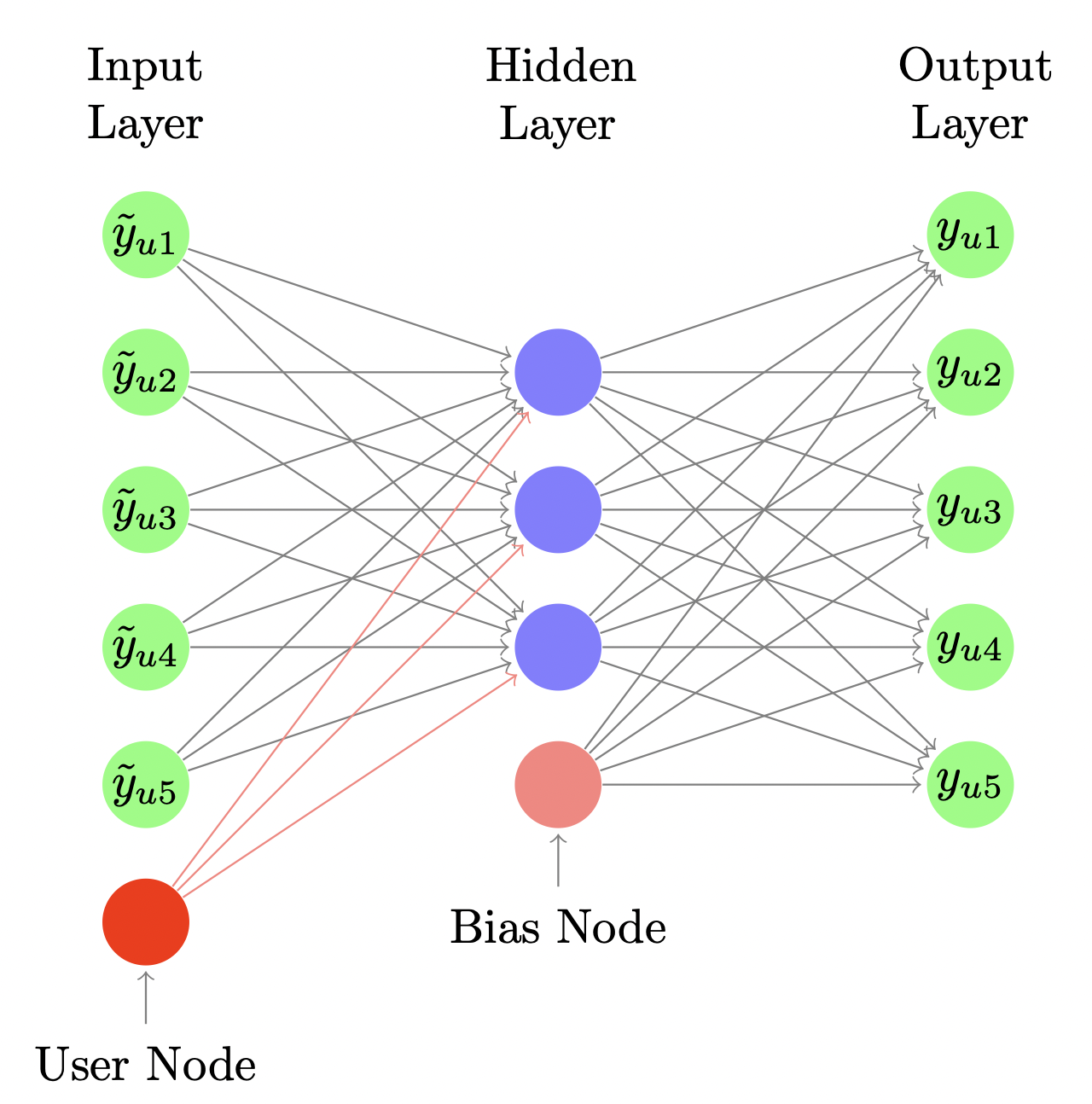
[출처] https://alicezheng.org/papers/wsdm16-cdae.pdf, Collaborative Denoising Auto-Encoders for Top-N Recommender Systems
Denoising Auto-Encoder라는 Auto-Encoder의 확장 버전을 사용한다고 볼 수 있다.
랜덤하게 input인 일부 상호작용을 0으로 수정하여 drop-out 함으로써 과적합을 예방하는 효과를 낳게끔한다.
이는 의도적으로 input에 noise를 삽입한 후 좀 더 복잡해진 오염된 input data에 관해서도 결과를 잘 reconstruction 할 수 있도록 하기 위함이다.
Input layer에 user node라고 하는 사용자의 id를 임베딩하여 생성한 것을 추가적으로 사용함으로써 이것이 어떠한 사용자를 나타내는지를 모델링하는 효과를 보이게 할 수 있다.
특히 MF에서의 user bias의 형태로 작동한다고 이해할 수도 있다.
여기서는 Top-K ranking 문제를 다루므로 interaction이 일어날 확률을 예측하는 형태로 결과가 나온다.
주로 implicit feedback을 다루는 NeuMF와 CDAE에서는 관측한 데이터 뿐만이 아니라 negative instance sampling을 활용하는데, 이는 실제 사용자가 사용하지 않았던 아이템 일부를 랜덤하게 샘플링해서 학습 과정에서 negative instacne에 관한 정보가 반영될 수 있도록 하는 것이다.
Multi-VAE
VAE(Variational Auto-Encoder)는 정확한 추론이 불가능한 상황에서 근접 추론을 위한 방법론 중 하나이며, deep generative model의 일종이다.
ELBO(Evidence Lower BOund) term들은 Auto-Encoder 관점에서 해석 가능하다.
$\mathbb{E}_{q_{\phi}(z|x)}[p_{\theta}(x|z)]$에 해당되는 term은 reconstruction error를 최소화하고, $D_{KL}(q_{\phi}(z|x)\|p(z))$에 해당되는 term은 variational distribution인 $q_{\phi}(z|x)$를 prior distribution인 $p(z)$과 유사하게 강화해주는 역할을 한다.
그래서 variational distribution인 $q_{\phi}(z|x)$는 확률적인 encoder 관점에서, original distribution인 $p_{\theta}(x|z)$는 확률적인 decoder의 관점에서 해석될 수 있다.
추천 시스템에서는 VAE를 interaction data의 reconstruction에 활용할 수 있다.
이때 기존 VAE와는 다르게 Multi-VAE에서는 데이터의 분포를 Gaussian이 아닌 다항분포(multinomial distribution)으로 모델링함으로써 아이템의 파라미터의 합이 1이 되게 하여 아이템들이 한정된 예산을 놓고 경쟁하는 현상을 표현할 수 있도록 한다.
또한 기존 VAE와는 달리 KL annealing을 사용함으로써 부분적으로 규제를 하는 테크닉을 사용한다.
여기서 KL annealing이란 학습 초기에는 loss에 곱해지는 정규항에 곱하는 파라미터의 값을 작게하여 latent 분포인 $z$에 의미 있는 정보가 담기게 하고, 뒤로 갈수록 정규항의 값을 키워서 prior distribution에 맞추도록 하는 것이다.
EASE(Embarrassingly Shallow Auto-Encoders)
일종의 Auto-Encoder이자 User-Free 모델로 볼 수 있다.
여기서는 학습되는 아이템 간 유사도를 구하는 행렬인 $W$ 대신에 $B$로 표기한다.
또한 자명한 해결 방법인 $B = I$가 되는 것을 피하기 위해 $B$의 대각 원소를 0으로 고정한다.
딥 러닝에서 학습할 때 SGD를 사용하지 않아도 바로 수식을 유도하여 파라미터를 구하는 close-form solution이어서 딥 러닝 프레임워크 말고 numpy로도 구현할 수 있다.
EASE에 관한 자세한 내용은 아래 포스트에서 구체적으로 서술했다.
Embarrassingly Shallow Autoencoders for Sparse Data 모델이 희소 데이터에 강한 이유
Embarrassingly Shallow Autoencoders for Sparse Data 모델은 왜 희소한 데이터에서 괜찮은 성능을 보일까? 한 달이라는 긴 시간동안 네이버 부스트캠프 AI Tech 3기에서 진행했던 Movielens 데이터 기반의 영화..
glanceyes.tistory.com
출처
1. 네이버 커넥트재단 부스트캠프 AI Tech RecSys Track
'AI > 추천 시스템' 카테고리의 다른 글
| 추천 시스템의 평가 방법과 실험에서의 데이터 분할 전략 (0) | 2022.04.26 |
|---|---|
| Side Information과 이를 사용하는 추천 시스템 (1) | 2022.04.20 |
| 추천 시스템에서의 Implicit Feedback (0) | 2022.04.18 |
| Embarrassingly Shallow Autoencoders for Sparse Data: EASE 모델이 희소 데이터에 강한 이유 (4) | 2022.04.16 |
| Memory-based와 Model-based Collaborative Filtering (0) | 2022.04.02 |
소중한 공감 감사합니다.