생성 모델(Generative Model)과 VAE 그리고 GAN
- -
Generative Model
Generative Model이란?
Discriminative Model과 Generative Model

일반적으로 머신러닝에서 모델을 크게 두 범주로 분류하자면 discriminative model과 generative model로 구분할 수 있다. Discriminative model은 데이터의 레이블링을 예측하는 것처럼 decision boundary를 잘 결정하는 것이 목표인 모델이며, 우리가 일반적으로 잘 아는 classficiation, segmentation, detection과 같은 task를 잘 수행하는 모델로 볼 수 있다.
그에 반해 생성 모델(generative model)은 기본적으로 어떠한 입력이 주어졌을 때 이를 모델에 통과하여 output을 내는데, 그 결과는 기존 input과 비교했을 때 핵심적인 내용은 유사하지만 noise 또는 stochastic variation이 추가될 수 있는 모델이라고 볼 수 있다. 그러나 더 정확한 표현으로 정리하자면, 우리가 설명하려는 학습 데이터의 분포를 따르면서 샘플을 샘플링하여 새로운 데이터를 생성하는 모델이다. 그러면 학습 데이터의 분포를 아는 게 중요한데, 일반적으로 학습 데이터가 주어졌을 때 이 데이터들이 어떠한 분포에서 나왔을 확률이 높은지를 구하는 maximum likelihood estimation으로 구한다.
Generative Model의 종류

'NIPS 2016: GAN tutorial' 문서에 보면 위와 같이 generative model을 분류했다. 앞서 generative model은 설명하려는 학습 데이터의 분포가 어떠한 분포에서 왔을 가능성이 높은지를 maximum likelihood로 구한다고 했는데, 모델링하려는 확률 분포를 명백한 수학적인 모델로 구하는 방법이 explicit density, 그러한 분포를 명백하게 구하지 않는 방법이 implicit density이다. Explicit density 방식에서도 두 가지로 분류할 수 있는데, tractable density 방법과 approximate density 방법으로 나눌 수 있다. Implicit density에서는 학습하려는 분포를 직접 구하기보다는 어떻게 그러한 분포를 잘 따르도록 샘플링할지에 관한 방법에 주목한다.
일반적으로 generative model이라면 자주 언급되는 모델은 바로 학습 데이터의 분포에 근사하는 분포를 구하는 VAE(Variational AutoEncoder)와 직접적인 분포를 구하지 않고 그러한 분포를 따르는 샘플링을 그럴 듯하게 수행하는 GAN(Generative Adversarial Network)가 있다. 그래서 위의 분류 그림을 보면 VAE는 explicit density의 approximate density 방법에 속하고, GAN은 implicit density에서 direct sampling을 수행하는 방법으로 분류되어 있다. 그러면 GAN과 VAE가 구체적으로 어떠한 모델이며, 이들이 각각 어떤 장단점을 지니고 있는지 간단히 짚고 넘어가자.
GAN(Generative Adversarial Model)
첫 번째는 바로 GAN(Generative Adversarial Model)이다. GAN은 이름에서도 알 수 있다시피 discriminator와 generator 모델에 관해 'adversarial' network를 구성하여 두 모델을 서로 번갈아 학습을 하여 최종적으로는 학습된 generator를 가지고 생성 모델로 사용하는 것이다. 여기서 generator는 noise에 해당되는 seed를 샘플링하여 자신이 생성한 이미지를 discriminator가 실제 이미지인 것처럼 속이게 만들기 위해 노력하고, discriminator는 주어진 입력이 실제 이미지인지 아니면 generator가 생성한 이미지인지를 잘 구분할 수 있도록 학습한다. 최종적으로 discriminator가 무엇이 generator가 생성한 데이터고 무엇이 진짜 데이터인지 구분하지 못하는 상태를 nash equilibrium에 도달했다고 말하고, 이러한 경쟁적인 학습 방식을 채택한 GAN은 높은 visual fidelity 덕분에 현재도 자주 사용되는 모델이다.
그러나 GAN은 학습이 다른 모델에 비해 상대적으로 불안정하다고 알려져 있다. 대표적으로 mode collapse 현상을 들 수 있는데, 이는 generator가 어떤 한 이미지만을 생성하는데도 불구하고 discriminator가 실제 이미지인 것으로 잘 속아서 generator가 다양한 이미지가 아니라 discriminator를 잘 속이기 위한 오직 하나의 이미지만을 생성하게 되는 문제이다. 이럴 경우 generator가 다채로운 이미지를 생성해야 한다는 목표에 위배되므로 좋은 현상이라고 볼 수 없다. 또한 GAN은 학습을 위해 optimization 하려는 loss의 종류가 많다. 이를 한 번에 정리하면 한 편의 긴 글이 될 정도로 학계에서 매우 많은 loss가 제안되었다. 이처럼 loss가 많이 나오는 것도 기존의 GAN의 학습이 불안정하다는 문제를 보여준다. 그리고 GAN은 static한 2D image에서 좋은 성능을 보이는 경우가 많고, 영상이나 3D로 넘어가면 상대적으로 좋지 못한 성능을 보이는 한정된 modality도 한계이다.
VAE(Variational AutoEncoder)
두 번째는 VAE(Variational AutoEncoder)이다. VAE는 명칭에서도 알 수 있듯이 autoencoder를 기반으로 하는 생성 모델인데, 그전에 autoencoder를 간단히 짚고 넘어갈 필요가 있다. Autoencoder는 입력을 encoder에 통과시켜서 latent space의 code로 보낸 뒤에, 거기서 바로 decoder를 통과하여 다시 복원된 이미지가 원래 이미지와 유사해지도록 학습하는 모델이다. 그런데 여기서 encoder에 통과시켜서 나오는 latent code를 decoder에 바로 통과시키지 않고, encoder에서 나온 output이 latent space에서 입력에 대응되는 조건부 latent distribution의 모수로 출력되도록 하면, 그 모수를 가지고 입력 이미지에 대응되는 조건부 latent distribution에서 latent code를 샘플링하여 이를 decoder에 넣어서 복원시킨 output이 나올 텐데, 그러면 그 이미지가 기존의 이미지와 핵심적인 정보는 유사하지만 샘플링 과정에서 noise가 추가되기 때문에 detail에서 차이가 있거나 다른 pose를 취하고 있는 등 새롭게 생성된 이미지가 나오는 것이다.
VAE의 장점은 상대적으로 간단한 모델이라는 것이다. Encoder 부분에서는 Fully-connected layer 또는 CNN를 여러 번 통과해서 저차원의 latent space로 보내고, 그 공간에서의 조건부 확률분포를 모델링하는 모수를 출력한다. 그 모수에 대응되는 latent distribution에서 latent code를 샘플링하여 이를 decoder에 통과시켜서 reconstruction된 output을 얻는 모델이다. 전반적인 학습 흐름이 크게 어렵지 않다. 그러나 VAE가 생성한 이미지의 visual fidelity는 GAN 계열의 모델보다 우위에 있지 않거나 이에 비해 상대적으로 좋지 않은 결과를 내는 것으로 알려져 있다. 그래서 fidelity가 중요한 모델에서는 VAE를 사용하는 일이 드물며, 주로 이미지를 reconstruction 하는 task에서 사용한다.
Generative Model의 특징
Generation
'그럴 듯한 가짜' 또는 '실제 데이터 셋에서 볼 수 있을 법한 input'을 만들어내는 모델이라고 볼 수 있다. 여기서 '그럴 듯하다'라는 것은 수학적으로 실제 데이터의 분포와 비슷한 분포에서 나온 데이터라는 걸 의미한다.
즉, 수학적으로 생성 모델의 목적은 실제 데이터 분포에 근사하는 것이며, 실제 데이터 분포에 근사하는 분포에서 샘플링된 값으로 새로운 데이터를 생성하는 것이다. 단순히 generation만 할 수 있는 건 implicit generative model이라고 한다.
Density estimation
Generative model은 어떤 이미지가 주어졌을 때 이것이 진짜 이미지인지 생성된 이미지인지를 판단할 수 있는 이상치 감지가 가능한 discriminator까지 포함한다.
Explicit model은 데이터 생성뿐만이 아니라 확률값을 얻어낼 수 있는 모델을 의미한다.
Unsupervised representation learning
이 특징이 generative model에 들어가는지는 논란이 있지만, 그래도 generative model이 할 수 있는 작업이다.
그러면 여기서 $p(x)$를 어떻게 구해야 하는지가 관건이다.
Basic Discrete Distributions
Bernoulli Distribution
Biased coin flip(던졌을 때 앞뒤가 나올 확률이 서로 다른 동전)을 예로 들 수 있다.
$D = \{\text{Heads, Tails}\}$
$P(X = \text{Heads}) = p$이면 $P(X = \text{Tails}) = 1 - p$이다.
그래서 이 분포를 표현하는 수는 $p$ 한 개이면 된다.
$X \sim Ber(p)$
Categorical Distribution
Biased m-sided dice(던졌을 때 면마다 나올 확률이 다른 주사위)를 예로 들 수 있다.
$D = \{1, \cdots, m\}$
각 면이 나올 확률은 $\sum_{i=1}^m p_i = 1$을 만족하는 $P(Y = i) = p_i$라고 정의할 수 있다.
이 분포를 표현하는 데 필요한 수는 $m - 1$개 필요하다.
RGB Joint Distribution
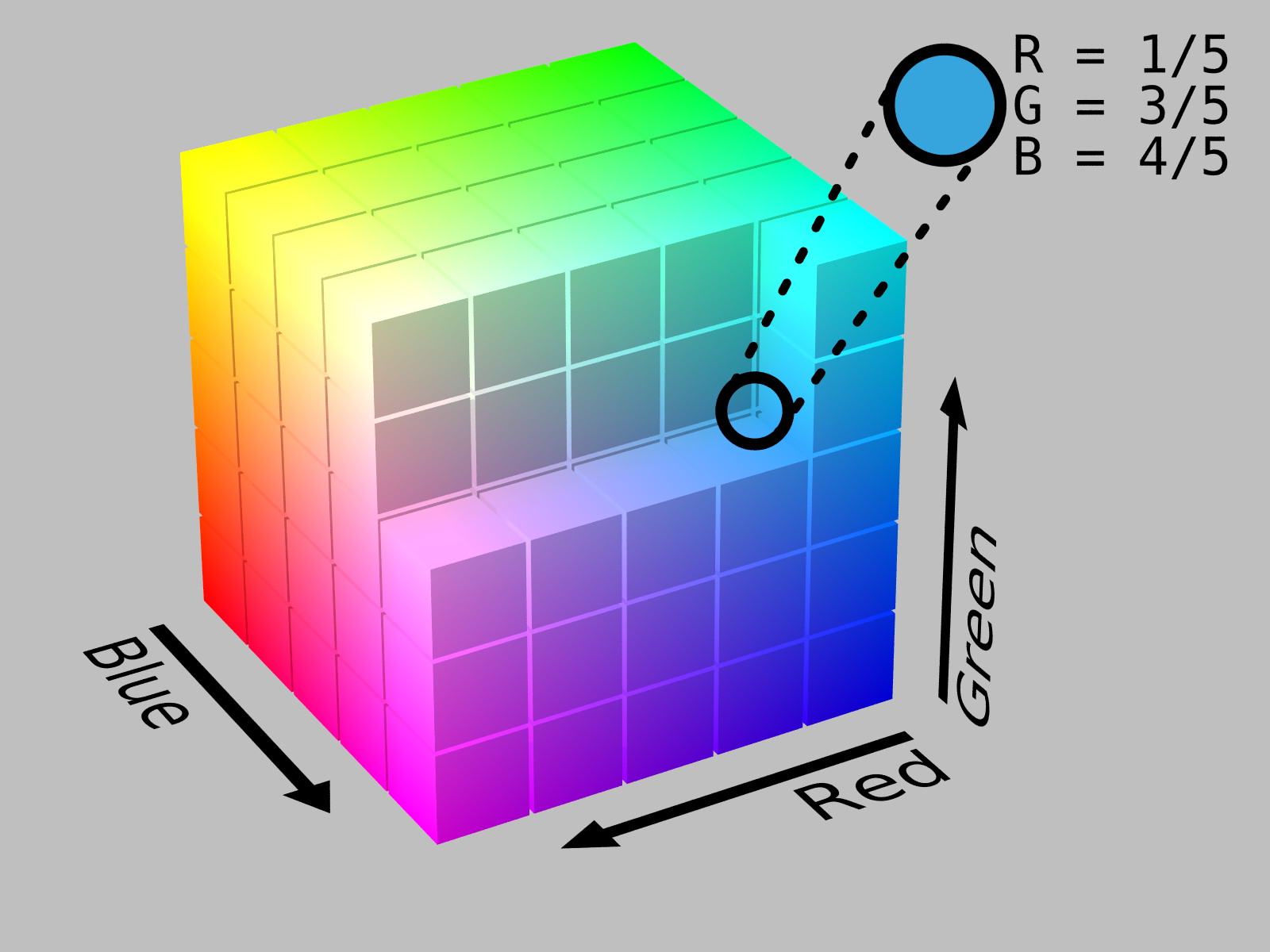
[출처] https://en.wikipedia.org/wiki/File:RGB_Cube_Show_lowgamma_cutout_b.png, SharkD
한 픽셀을 표현하는 데는 RGB의 세 개의 값이 필요하다.
$(r, g, b) \sim p(R, G, B)$
이 분포를 표현하는 데 필요한 파라미터 수는 $256 × 256 × 256 - 1$이다.
Binary Image
$X_1, \cdots, X_n$까지의 $n$개의 binary pixel이 있다고 가정하면, 가능한 경우의 수는 $2^n$이다.
이때 필요한 파라미터 수는 $2^n - 1$이다.
기억해야 할 점은 기계학습에서 파라미터의 수가 많아지면 많아질수록 generalization performace가 낮아진다.
$n$개의 binary pixel이 모두 independent하다면 어떻게 될까? (사실 유의미한 가정은 아니다.)
$p(x_1, \cdots, x_n) = p(x_1) p(x_2) \cdots p(x_n)$
가능한 경우의 수는 $2^n$이지만, 필요한 파라미터 수는 $n$개가 된다.
그러나 이렇게 될 경우 표현력이 떨어지게 된다.
Conditional Independence
조건부 확률 가정을 어떻게 하는가에 따라 파라미터의 수가 달라지며, 이는 모델에 큰 영향을 준다.
Chain Rule
Bayes Rule
Conditional Independence
$z$가 주어졌을 때 $x$와 $y$가 independent 하면, $p(x|y,z) = p(x|z)$를 만족한다.
즉, $x \bot y | z$이면, $p(x|y,z) = p(x|z)$이다.
Chain rule과 잘 조화시키면 condition에 해당되는 부분을 날려줄 수도 있다.
어떠한 가정도 없이 chain rule을 사용하면 joint distribution을 conditional distribution으로 표현해주는 것밖에 없으므로 fully dependent model과 같은 수의 파라미터를 가진다.
$p(x_1)$: 파라미터 1개
$p(x_2|x_1)$: 파라미터 2개 ($p(x_2|x_1= 0)$일 때 1개, $p(x_2|x_1 = 1)$일 때 1개)
$p(x_3|x_1, x_2)$: 파라미터 4개
필요한 전체 파라미터의 수는 $1 + 2 + 2^2 + \cdots + 2^{n-1} = 2^n - 1$이므로 fully dependent model일 때와 같다.
그런데 만약에 $X_{i+1} \bot X_1, X_2, \cdots, X_{i-1} |X_i$ (Markov Assumption)처럼 $i+1$번째 픽셀은 $i$번째 픽셀에만 dependent하고, 1부터 $i-1$번째 픽셀에는 independent하다고 가정한다.
그러면 $p(x_1, \cdots, x_n) = p(x_1) p(x_2|x_1) p(x_3|x_2) \cdots p(x_n|x_{n-1})$를 만족한다.
이때 필요한 파라미터 수는 $1 + 2 + 2 + \cdots + 2$이므로 $2n - 1$이다.
Auto-regressive model은 이러한 conditional independency를 이용한다.
Auto-Regressive Model
28 × 28 크기의 binary 픽셀이 있다고 가정한다.
$p(x) = p(x_1, \cdots, x_{784})$ over $x \in \{0, 1\}^{784}$
$p(x)$를 chain rule에 의해 parameterize하면 다음과 같다.
$p(x_{1:784}) = p(x_1) p(x_2|x_1) p(x_3|x_{1:2}) \cdots p(x_{784}|x_{1:783})$
이처럼 일반적으로 하나의 데이터가 이전 데이터에 dependent한 모델을 auto-regressive model(AR(1))이라고 한다.
이 random한 픽셀들에 순서를 매기는 것이 필요하다.
어떤 식으로 conditional independence를 주는지에 따라 전체 모델의 structure가 달라질 수 있다.
Neural Autoregressive Density Estimator (NADE)
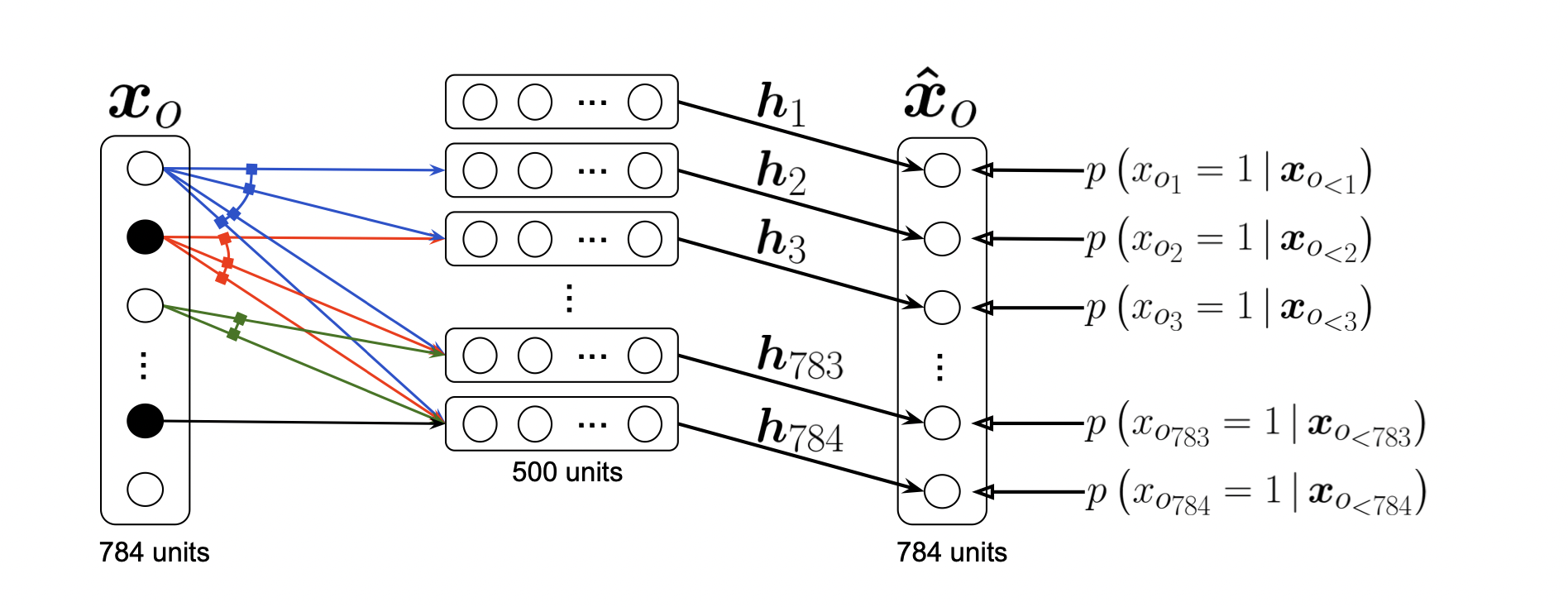
[출처] https://www.jmlr.org/papers/volume17/16-272/16-272.pdf, Neural Autoregressive Distribution Estimation
1에서 $i$번째 픽셀로 갈수록 neural network의 입력 수가 늘어나므로 neural network의 weight가 계속 커진다.
NADE는 explicit 모델이어서 단순 generation뿐만이 아니라 임의의 input에 관해서도 확률을 계산할 수 있다.
즉, 임의의 input에 관해 독립적으로 확률을 explicit하게 계산할 수 있다.
Continuous한 random variable을 모델링 할 경우 Gaussian distribution을 사용한다.
Pixel RNN(Recurrent Neural Network)
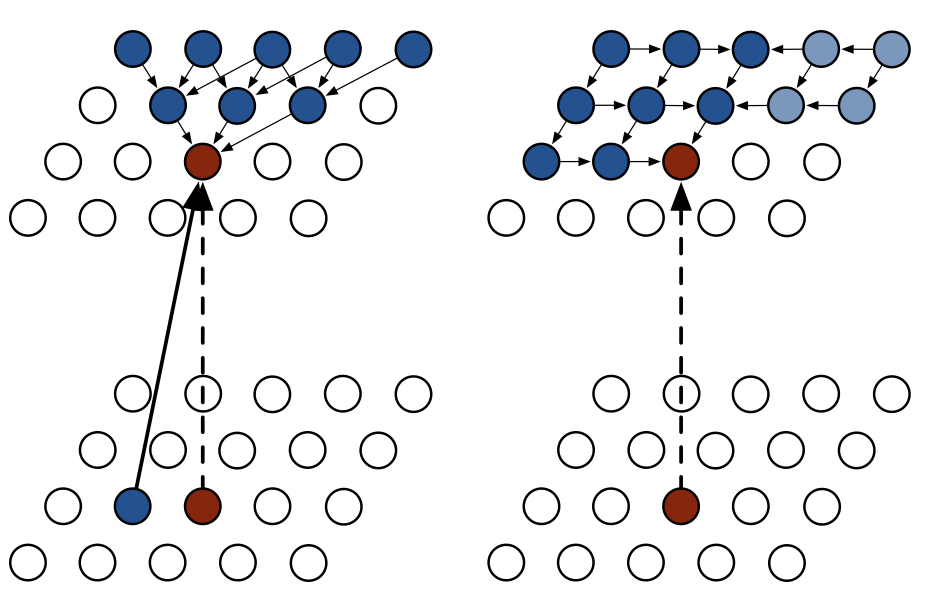
[출처] https://arxiv.org/pdf/1601.06759.pdf, Pixel Recurrent Neural Networks
RNN을 사용하여 auto-regressive model을 정의할 수도 있다.
$n × n$인 RGB image의 경우는 다음과 같다.
$i$번째 픽셀은 1부터 $i-1$번째까지의 픽셀도 고려할 뿐만이 아니라 $i$번째 픽셀의 R,G,B 값도 고려한다.
Pixel RNN의 ordering을 어떻게 하느냐에 따라 두 가지로 나눌 수 있다.
- Row LSTM
- Diagonal LSTM
위의 그림에서 왼쪽이 Row LSTM, 오른쪽이 Diagonal LSTM 방식을 도식화한 것이다.
Latent Variable Models
Auto-Encoder(AE)는 generative model일까? No!
- VAE와 AE는 목적이 전혀 다르다.
- AE의 목적은 어떤 데이터를 잘 압축하는것, 어떤 데이터의 특징을 잘 뽑는 것, 어떤 데이터의 차원을 잘 줄이는 것이다.
- AE는 학습을 진행하고, 나중에 decoder 부분을 떼어 버린다.
- 이후 input data의 중요한 정보만 담고 있는 $z$로 input data를 예측을 하면 원래보다는 결과가 나아질 것이다.
- 반면 VAE의 목적은 Generative model으로 어떤 새로운 데이터를 만들어내는 것이다.
- 즉, VAE는 generative model이고, AE는 generative model이 아니다.
Variational Auto-Encoder (VAE)
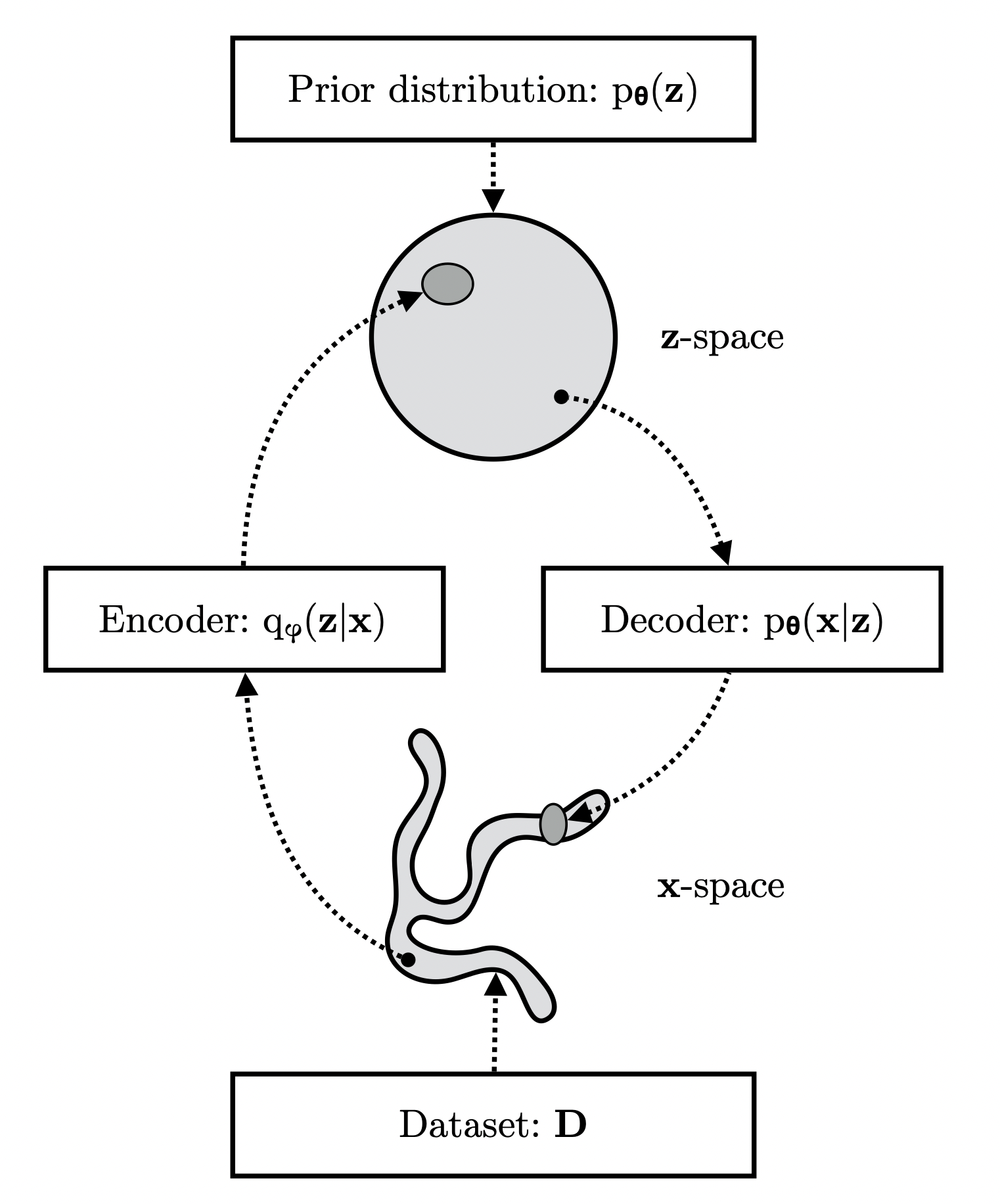
[출처] https://pure.uva.nl/ws/files/17891313/Thesis.pdf, Variational Inference and Deep Learning: A New Synthesis
Variational Auto-Encoder
Unsupervised Learning은 데이터의 label이 주어지지 않더라도 input 데이터가 주어졌을 때 해당 데이터가 어떠한 label에 속하는지를 알아낼 수 있도록 하는 방법이다.
꼭 label이 아니어도 feature 값으로 생각할 수도 있는데, 어떤 데이터의 정답 feature 값이 주어지지 않더라도 해당 데이터가 어떠한 feature 값을 가져야 하는지 알아낼 수 있는 것이다.
그런데 일반적으로 손실함수인 loss function을 줄이는 방향으로 모델을 학습시켜야 하는데, 상식적으로 정답 데이터가 주어지지 않으면 실제 정답과 예측에 대한 loss function을 구할 수가 없다.
이를 해결하고자 하는 방법이 variational auto-encoder이다.
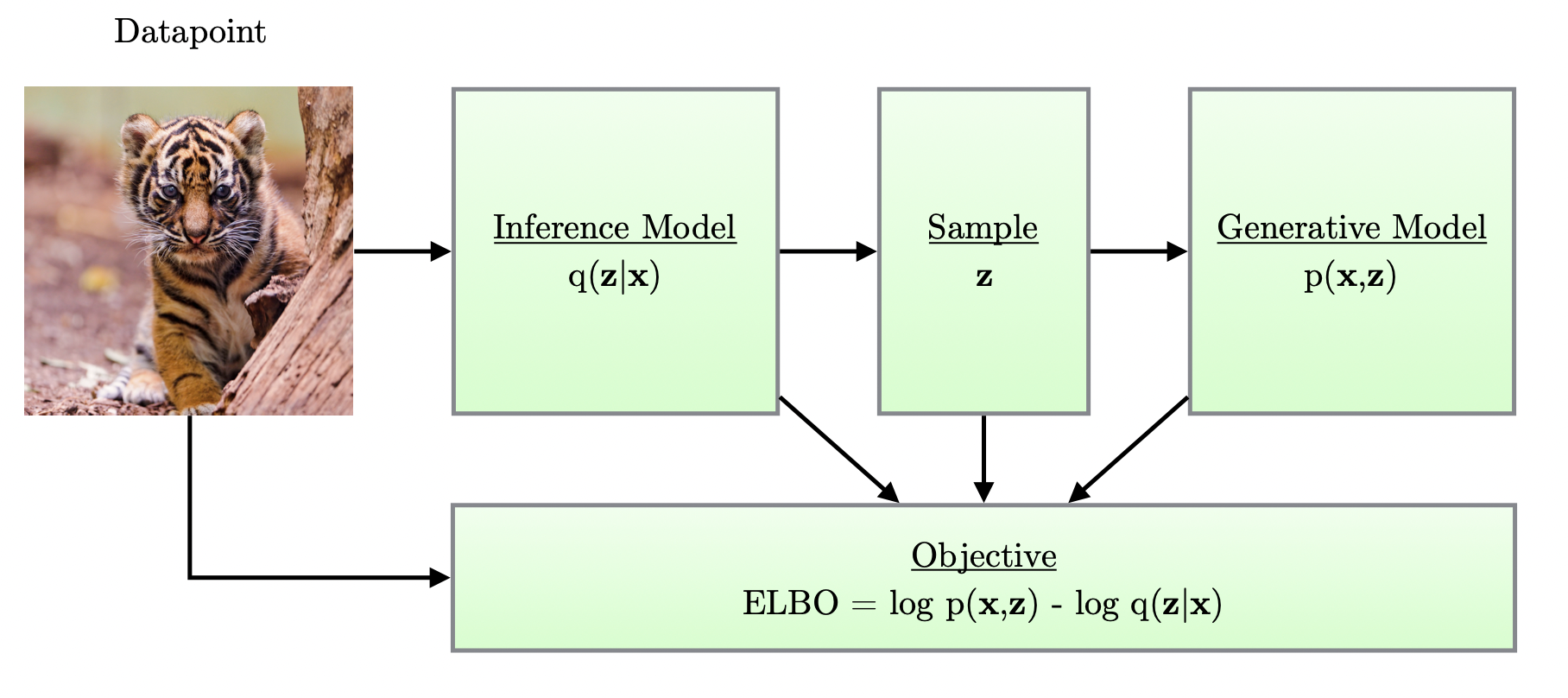
[출처] https://pure.uva.nl/ws/files/17891313/Thesis.pdf, Variational Inference and Deep Learning: A New Synthesis
예를 들어 이미지를 학습시킨다고 가정해보면, variational auto-encoder에서는 이미지 $x$를 encoder에 넣어서 $x$보다 차원이 작은 $z$라는 결과를 구하고, 이 $z$를 바탕으로 decoder에 통해 새로운 이미지를 reconstruction 하는 것이다.
$z$의 차원이 $x$보다 적다는 말은 $z$는 $x$에 대한 중요한 정보(core data)만을 담고 있어야 한다는 의미이고, 이로 인해 $z$를 가지고 $x$와 유사한 새로운 input data인 $\hat{x}$를 만들어 낼 수 있는 것이다.
그러면 loss function을 $\|x - \hat{x}\|^2$로 설정하여 이를 최소화하는 방향으로 모델을 학습시키면, $z$에는 결국 reconstruction하기 위한 중요한 정보를 담게 할 수 있다.
VAE는 완전히 input과 똑같은 이미지를 생성하고 싶은 것이 아니라 유사하지만 조금은 다른 조정된(controlled) 이미지를 생성하고 싶은 것이므로 확률분포를 이용한다.
Variational Inference(변분추론, VI)
The goal of VI is to optimize the variational distribution that best matches the posterior distribution.
Posteroir distribution(사후 확률분포)을 찾는 것이 목표이다.
아래는 이 포스트를 쓰면서 자세히 참고한 자료 링크이다.
https://ratsgo.github.io/generative%20model/2017/12/19/vi/
변분추론(Variational Inference) · ratsgo's blog
이번 글에서는 Variational Inference(변분추론, 이하 VI)에 대해 살펴보도록 하겠습니다. 이 글은 전인수 서울대 박사과정이 2017년 12월에 진행한 패스트캠퍼스 강의와 위키피디아 등을 정리했음을 먼
ratsgo.github.io
Posterior Distribution
Posterior distribution인 $p_{\theta}(z|x)$은 observation이 주어졌을 때, 관심 있어하는 random variable의 확률분포이다.
위에서 $z$는 latent vector, $x$는 input이다.
Variational Distribution(Latent Distribution)
일반적으로 posterior distribution을 구하는 것은 불가능하므로 이를 최적화하여 posterior distribution에 근사할 수 있는 확률분포 $q_{\phi}(z|x)$를 찾는다.
KL(Kullback-Leibler) Divergence metric을 사용해서 posterior distribution과 variational distribution의 차이를 줄일 수 있다.
Posterior distribution이 무엇인지도 모르는데, variational distribution을 어떻게 찾을 수 있을까?
Posterior distribution인 $p(z|x)$와 variational distribution인 $q_{\phi}(z|x)$의 KL divergence를 줄이는 것이 목적이지만, 이것이 어려우므로 ELBO(Evidence Lower BOund)를 키움으로써 반대급부로 KL divergence를 줄일 수 있다.
ELBO는 reconstruction term과 prior fitting term으로 유도가 가능하다.
Reconstruction term은 encoder를 통해서 input을 latent space로 보내고 다시 decoder로 돌아오는 reconstruction loss을 줄이는 것이다.
Latent space는 input 대상을 잘 설명할 수 있는 공간이며, input의 feature 중 일부는 다른 feature의 조합으로 표현 가능해서 불필요할 수 있으므로 latent space는 일반적으로 실제 space보다 작다.
Prior fitting term은 input을 latent space로 올렸을 때 이루는 latent distribution을 prior distribution과 유사하도록 강화해주는 것이며, KL Divergence를 활용한다.
Auto-encoder는 input 자신을 언제든지 reconstruct할 수 있는 z를 만드는 것이 목적이라면, VAE는 input이 만들어지는 확률 분포를 찾는 것이 목적이다.
Variational Auto-Encoder의 특징
어떤 입력이 주어졌을 때 이 입력을 latent space로 보내고 무언가를 찾은 후 이를 reconstruction하는 term으로 만들어지는데, latent space 상의 posterior distribution으로 $z$를 sampling을 하고 이를 decoder에 통과시켜서 나오는 output 값이 generated result라고 보는 것이다.
비문이 많아서 이해하기 어려운데, 요약하자면 입력값 $x$를 encoder에 통과시키고, encoder의 결과로 나온 $\mu$와 $\sigma$로 된 정규 분포에서 latent variable인 $z$를 샘플링하여 다시 이를 decoder에 통과시켜 새로 만들어진 $x'$를 얻는 것이다.
Auto-encoder는 input이 encoder를 통해 latent space로 간 후 다시 decoder를 통과하여 output으로 나오므로 latent space에서의 사후 확률분포를 고려하지 않아서 엄밀한 의미로서 generation model이 아니다.
Variational Auto-encoder의 한계
Intractable model이어서 Explicit한 model이 아니다.
여기서 intractable이란 문제를 해결하기 위해 필요한 시간이 문제의 크기에 따라 지수적으로(exponential) 증가한다면 그 문제는 난해(intractable)하다고 한다.
Prior fitting term은 미분 가능해야 하므로 다양한 latent prior distribution을 사용하기 어려워서 gaussian distribution을 주로 사용한다.
그래서 대다수의 경우 isotropic Gaussian을 사용한다. (모든 output dimension이 independent함을 의미한다.)
Adversarial Auto-Encoder
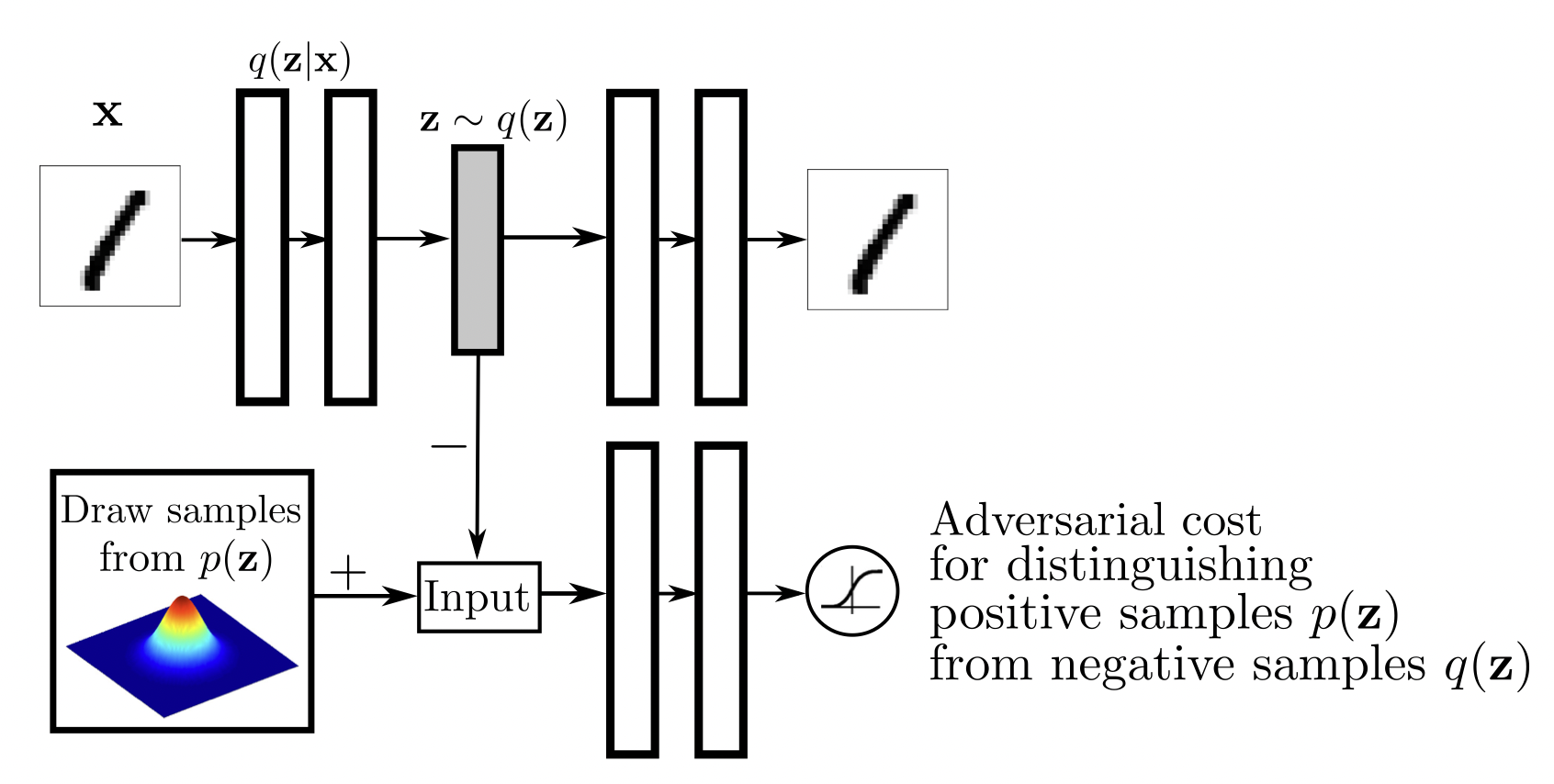
[출처] https://arxiv.org/pdf/1511.05644.pdf, Adversarial Autoencoders
GAN을 활용해서 latent distribution 사이의 분포를 맞춰주는 것이다.
Variational auto-encoder의 prior fitting term을 GAN objective으로 바꾼 것과 같다.
Generative Adversarial Network (GAN)
Generative Adversarial Network(GAN)
Generator는 discriminator를 잘 속이려고 하고, discriminator는 generator가 만든 input 중에서 찾고자 하는 것을 잘 구별하게 하여 이를 반복하면서 결과적으로 discriminator와 generator의 성능을 높이는 것이다.
다시 말해, generator와 discriminator라는 두 개의 모델을 적대적(adversarial)으로 경쟁시키며 발전시키는 것이며, generator와 discriminator라는 두 명의 player가 서로 minmax game을 하는 것으로 볼 수 있다.
Discriminator 입장에서는 위의 식을 만족하도록 최적화 해야한다.
이를 항상 최적화시키는 discriminator는 다음과 같이 요약할 수 있다.
이를 통해 나오는 결과는 다음과 같다.
우리가 만들었다고 생각하는 true data distribution과 학습한 generator 사이의 Jenson-Shannon Divergence(JSD)를 최소화하는 것을 의미한다.
GAN을 활용한 여러 모델
DCGAN
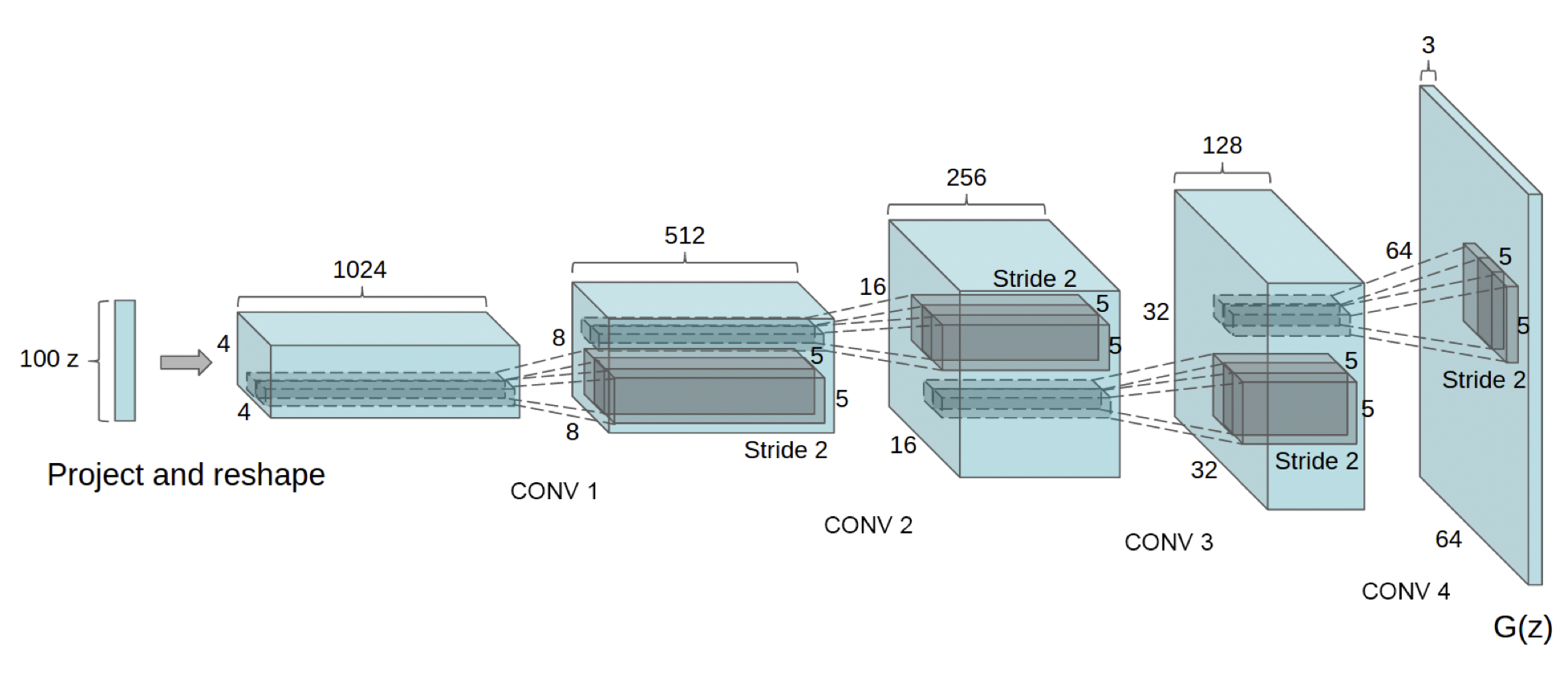
[출처] https://arxiv.org/pdf/1511.06434.pdf, Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks
이미지 도메인에서 GAN을 활용한 케이스이다.
Info-GAN

[출처] https://arxiv.org/pdf/1606.03657.pdf, InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets
Class라는 것을 random하게 집어 넣어서 결과론적으로 generation할 때 generator가 특정 모드에 집중할 수 있도록 하는 것이다.
Puzzle-GAN
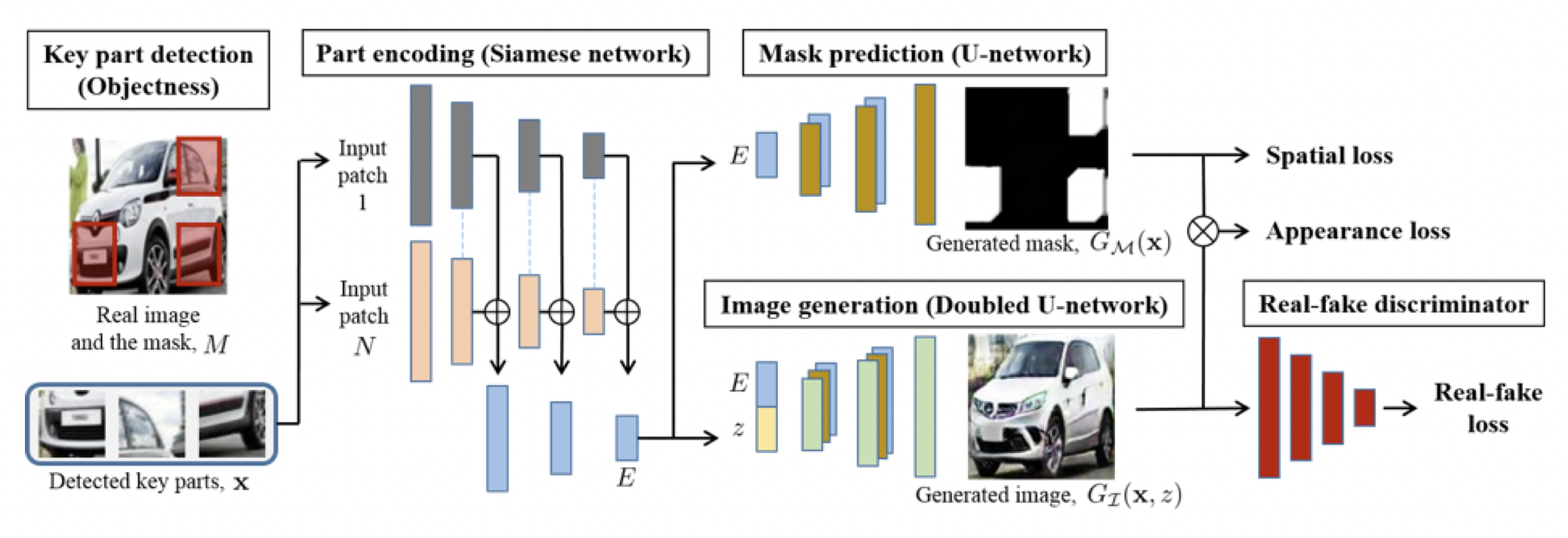
[출처] https://arxiv.org/pdf/1703.10730.pdf, Unsupervised Holistic Image Generation from Key Local Patches
Image 안의 서브 패치를 통해서 원래 이미지를 복원하는 모델을 GAN으로 만든 것이다.
CycleGAN
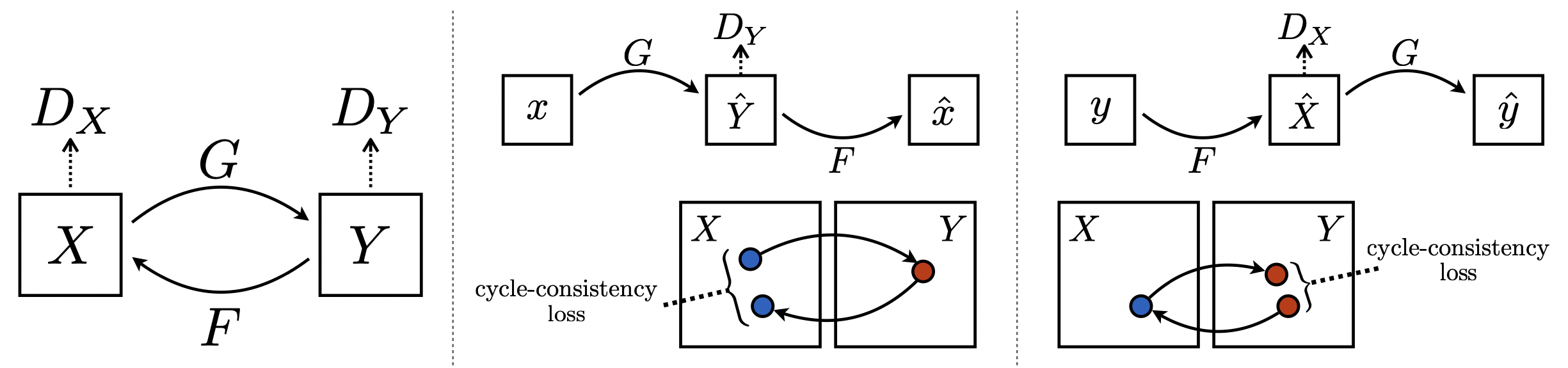
[출처] https://arxiv.org/abs/1703.10593, Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks
Cycle-consistency loss를 통해 둘 이상의 이미지 사이의 도메인을 바꿀 수 있는 것이다.
Progressive-GAN
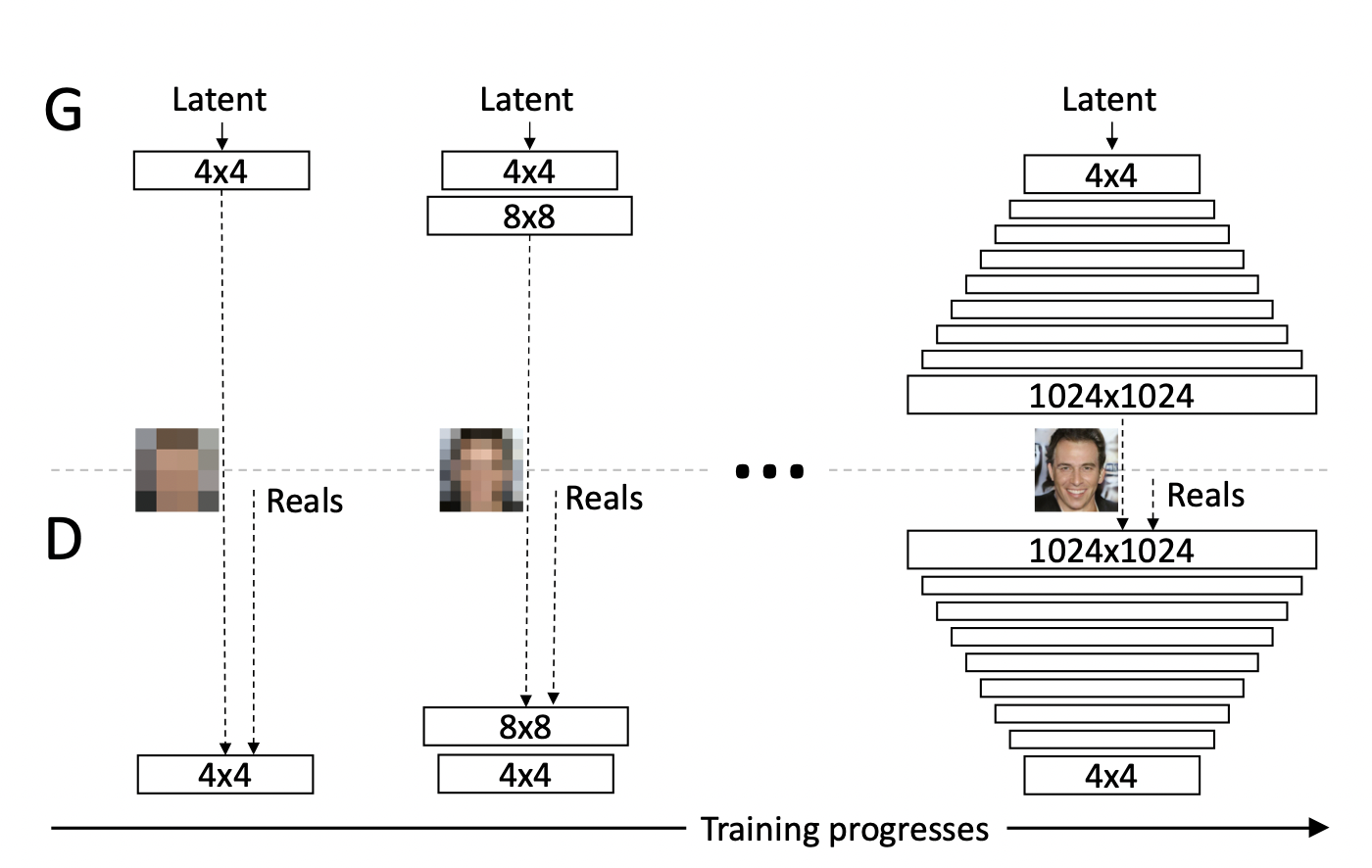
[출처] https://arxiv.org/pdf/1710.10196.pdf, Progressive Growing of GANs for Improved Quality, Stability, and Variation
고차원의 이미지를 생성하는 데 최적화된 모델이다.
작은 크기의 이미지부터 큰 이미지의 크기를 차례로 키워서 만드는 아이디어를 사용했다.
출처
1. 네이버 부스트캠프 AI Tech 기초 인공지능 강의 (Generative Model)
'AI > AI 기본' 카테고리의 다른 글
| Transformer의 Self Attention에 관한 소개와 Seq2Seq with Attention 모델과의 비교 (0) | 2022.07.23 |
|---|---|
| Attention 기법을 사용한 Seq2Seq with Attention (0) | 2022.07.14 |
| Self-Attention을 사용하는 Transformer(트랜스포머) (0) | 2022.02.17 |
| 순차 데이터와 RNN(Recurrent Neural Network) 계열의 모델 (0) | 2022.02.17 |
| 딥 러닝에서의 일반화(Generalization)와 최적화(Optimization) (0) | 2022.02.16 |
소중한 공감 감사합니다.