AI/CV

NeRF: 2D 이미지를 3D 이미지로 Reconstruction하여 Novel View Synthesis이 가능한 Neural Radiance Fields

들어가기 전에

어떤 대상의 2D 이미지를 가지고 3D 이미지로 reconsturction하여 새로운 각도에서 본 이미지를 얻는 novel view synthesis를 수행하기 위한 방법이 꾸준히 연구되어 왔다. 그중에서 volumetric rendering 과정에서 neural network인 MLP를 사용하여 괄목할 만한 view synthesis 성능을 보인 NeRF가 크게 주목을 받았다. 현재는 더 발전된 방법들이 많이 제안되었지만, NeRF(Neural Radiance Fields)에서 volumetric rendering을 최적화하기 위해 시도한 방법을 익혀두고 이를 바탕으로 어떻게 발전되어 왔는지 그 흐름을 공부해 둘 필요가 있어 보였다. 그래서 이번 논문 리뷰에서는 NeRF에서 주목해야 할 만한 여러 방법론에 관해 핵심을 위주로 간단히 정리하고자 한다.

NeRF(Neural Radiance Fields)란?

[출처] https://github.com/yenchenlin/nerf-pytorch

NeRF는 sparse한 2D 이미지를 가지고 volumetric rendering에서 사용하는 continuous volumetric scene function을 최적화하여 새로운 각도에서 본 이미지를 생성하는 데 있어서 2020년 당시 state-of-the-art의 결과를 보인 방법론이다. 이전까지만 해도 neural network를 사용해서 novel view synthesis를 수행한 결과가 그리 좋지 않았는데, NeRF가 나오면서 3D reconstruction 분야의 한 획을 그었다고 평할 정도로 좋은 성능을 보인다고 한다.

AI 분야는 1년만 시간이 지나도 구식이 되는 경우가 많은데, NeRF는 현재 글 작성 시점 기준으로 나온 지 꽤 되었고 그동안 이에 관해 자세하고 쉽게 설명한 리뷰가 많아서 일일이 논문의 모든 부분을 상세히 기술하는 건 크게 의미가 있지 않다고 느꼈다. 그래서 이 글에서는 핵심적인 부분 위주로 배경지식과 왜 이러한 방법을 사용했는지와 함께 오해할 수 있는 부분에 관해 자문자답하는 식으로 서술하고자 하며, PyTorch로 구현된 코드도 간단히 살펴보고자 한다. 참고한 코드 github URL은 다음과 같다.

https://github.com/yenchenlin/nerf-pytorch

GitHub - yenchenlin/nerf-pytorch: A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces the results.

A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces the results. - GitHub - yenchenlin/nerf-pytorch: A PyTorch implementation of NeRF (Neural Radiance Fields) that reproduces ...

github.com

개인적으로 이 논문에서 주목할 만한 부분을 세 가지로 정리하면 다음과 같다.

어떠한 과정에서 neural network를 어떤 목적으로 사용했는지
Volume rendering을 위한 함수를 어떻게 정의했는지
Volume rendering 과정에서 ray 위의 점들을 어떻게 샘플링할 것인지

Novel View Synthesis는 언제 사용될 수 있을까?

일반적으로 2D 이미지에 3D object를 표현하는 경우 그 대상의 정해진 특정 방향에서 바라 본 2D 이미지를 그대로 다루기보다는 3D object의 mesh, voxel grid 등 3D 정보를 저장하여 다루는 경우가 많다. 이는 그 3D object를 어떠한 방향에서 바라보느냐에 따라 2D 이미지에 어떻게 렌더링 되는지가 달라질 수 있어서다. 그러나 3D object의 정보를 저장하고 처리하는 데 필요한 리소스와 연산량이 많아져서 고성능의 컴퓨팅이 요구될 수 있다.

만약 그 3D object를 앞에서 바라 본 모습만 저장하고 이를 novel view synthesis를 통해 다양한 각도에서 본 모습을 렌더링 할 수 있으면 필요한 컴퓨팅 리소스가 크게 줄 수 있지 않을까? 즉, 3D object를 임의의 방향에서 바라볼 때 어떠한 모습인지에 관해 학습시킨 neural network만 가지고 있다면, 3D object 그 자체의 정보가 없어도 새로운 view에 관한 2D image를 보여줄 수 있다.

NeRF 모델 살펴보기

NeRF에서 Deep Neural Network를 어떻게 사용했는가?

먼저 NeRF에서 사용한 deep neural network가 어떻게 사용되었는지를 살펴보고, 왜 논문에서 이처럼 구현했는지 그 이유를 정리하려고 한다.

우리가 현실에서 어떤 3D object를 특정 방향에서 핀홀(pinhole) 카메라를 통해 볼 때, 3D object를 온전히 그대로 눈으로 받아들이지 않고 object를 구성하는 각각의 point에서 반사된 광선(ray)을 받아들인다. 카메라 또는 사람의 망막은 2차원으로 되어 있고, 이를 구성하는 각각의 픽셀에 어떠한 빛이 들어오는지에 따라 그 픽셀의 색이 결정되는데, 이는 다시 말해 그 픽셀에 들어오는 ray 위에 있는 점들이 어떠한 색상과 밀도를 띠는지를 적분한 결과에 의해 픽셀의 색과 투명도가 결정된다는 것이다.

어렵게 서술되어서 그렇지만 그림과 같이 공부하면 쉽게 이해할 수 있다. 예를 들어, 다음과 같이 카메라의 핀홀을 통해 픽셀로 들어오는 ray가 있다고 가정해 보자. 그러면 ray 위의 점들에서 주황색 point들을 A, 초록색 point들을 B라고 하자. A는 공기 중에 있으므로 밀도가 낮고, B는 직육면체인 object에 있으므로 밀도가 높다. 그러면 A와 B 중 픽셀의 색을 결정하는 데 더 많은 영향을 미치는 것은 무엇일까? 바로 B이다. 밀도가 낮으면 그만큼 투명도가 높고, 반대로 밀도가 높으면 투명도가 낮아서 ray의 색에 영향을 덜 미치게 된다.

그러면 B 중에서 픽셀의 색에 가장 영향을 많이 끼치는 point는 무엇일까? Ray가 처음 직육면체 object에 도달할 때 만나게 되는 지점일 확률이 높다. 이러한 직관을 미리 이해하고 NeRF에서 소개된 방법을 공부하면 좀 더 빠르게 이해할 수 있을 것이다.

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Figure 2

NeRF에서 deep neural network로 무엇을 하는지 궁금할 수 있는데, 바로 3차원 공간 상의 임의의 point 위치와 이를 바라보는 ray의 viewing direction을 가지고 해당 point에서의 density와 color를 예측하는 것이다. 다시 말해, NeRF에서는 ray 위에 존재하는 실제 3차원 공간상의 point마다 밀도와 색이 어떠한지를 학습하기 위해 각 fully-connected layer로 구성된 deep neural network를 사용한다. 이때 input은 ray 위에 있는 point의 3D 공간상의 좌표 $(x, y, z)$와 그 ray가 뻗어 나가는 방향이자 2D 이미지에서 해당 point를 바라보는 방향(viewing direction) $(\theta, \phi)$이다. 그리고 output은 point가 위치한 곳의 volume density $\sigma$와 그 point가 어떠한 색으로 보일 지를 의미하는 view-dependent emiited radiance $c$이다.

이쯤 되면 머리가 복잡해질 수 있는데, 여기까지가 대략적인 아이디어고 이제부터 의문이 들 수 있는 점을 하나씩 정리해보고자 한다.

Point의 3차원 좌표인 $(x, y, z)$는 어떻게 구하는 것인가?

Point의 좌표인 $(x, y, z)$는 직접 명시적으로 데이터로 주어지지는 않고, ray origin과 viewing direction을 unit vector로 변환한 것을 가지고 좌표를 구한다. Ray origin은 카메라를 촬영한 3차원 좌표이고, viewing direction은 object를 찍은 방향으로 뻗어 나가는 ray의 방향을 의미한다. Ray origin과 viewing direction를 가지고 해당 ray 위에 있는 임의의 point들의 world coordinate 좌표인 $(x, y, z)$를 구하는 것이며, 처음부터 $(x, y, z)$가 주어지는 것은 절대 아니다.

Ray origin과 viewing direction을 이용하면 ray 위의 point 좌표는 쉽게 구할 수 있다. 앞서 viewing direction을 $(\theta, \phi)$라고 표현했는데, 일반적으로 이를 unit vector로 나타내는 건 어렵지 않다. 한 축 방향으로의 unit vector에 rotation matrix를 적용한 후 벡터의 크기를 1로 정규화해 주면 해당 방향으로의 unit vector이다. 그러나 이 논문에서는 하술할 intrinsic parameter와 extrinsic parameter를 이용하여 각 픽셀별로 viewing direction을 계산했다. 여기서 짚고 넘어가고자 하는 바는 viewing direction과 벡터는 서로 자유자재로 변환할 수 있다는 것이다.

Ray origin이 world coordinate에서의 특정 좌표이고 viewing direction에 관한 unit vector을 구한 상태라면 ray 위에 존재하는 point의 좌표는 ray origin에서 시작하여 unit vector 방향으로 실수배만큼 이동한 위치로 구할 수 있다.

좀 더 쉬운 이해를 위해 2차원 평면 상에 그려서 나타냈지만, 3차원에서도 성립하는 내용이다. 3차원이라면 초점 $o$와 unit vector $d$는 각각 3차원 좌표와 벡터로 주어지고, $o$에서 벡터 $d$ 방향으로 $t$만큼 실수배 이동한 곳의 3차원 좌표 $(x, y, z)$가 바로 $r(t)$와 같다.

def render_rays(ray_batch,network_fn,
                network_query_fn,
                N_samples,
                retraw=False,
                lindisp=False,
                perturb=0.,
                N_importance=0,
                network_fine=None,
                white_bkgd=False,
                raw_noise_std=0.,
                verbose=False,
                pytest=False):
                
    N_rays = ray_batch.shape[0]
    rays_o, rays_d = ray_batch[:,0:3], ray_batch[:,3:6] # [N_rays, 3] each
    viewdirs = ray_batch[:,-3:] if ray_batch.shape[-1] > 8 else None
    bounds = torch.reshape(ray_batch[...,6:8], [-1,1,2])
    near, far = bounds[...,0], bounds[...,1] # [-1,1]

    t_vals = torch.linspace(0., 1., steps=N_samples)
    
    # 중략

    pts = rays_o[...,None,:] + rays_d[...,None,:] * z_vals[...,:,None] # [N_rays, N_samples, 3]

run_nerf.py 파일 코드에서 render_rays 함수에서 ray origin인 rays_o와 ray direction인 rays_d를 받아서 point들의 좌표인 pts를 구하는 부분이 이에 해당된다. z_vals는 t_vals를 가지고 샘플링하면서 나온 변수인데, 이는 샘플링하는 부분에서 서술할 예정이다. 여하튼 rays_o 좌표에서 rays_d 벡터 방향으로 z_vals 실수배만큼 이동한 곳의 좌표가 point들의 좌표인 pts이다.

Ray origin과 ray direction은 어떻게 구하는가?

논문에서 구현한 바에 의하면 ray origin과 ray direction은 intrinsic parameter에 관한 행렬인 $K$와 extrinsic parameter에 관한 행렬을 사용하여 구한다. 이에 관한 computer vision 배경 지식이 필요한데, 간단히 설명하고 넘어가려고 한다.

2D 이미지는 실제 3차원 공간상에 있는 점들을 이미지 평면에 투영(projection)시킨 것과 같으며, 투영하는 과정에서 projection matrix를 사용한다. 그러면 이 행렬을 사용하여 이미지 좌표계와 real world 좌표계를 자유자재로 변환할 수 있음을 유추할 수 있다. 이때 projection matrix로 고려되는 게 바로 intrinsic과 extrinsic parameter이다. Intrinsic parameter는 렌즈와 초점(focal point) 사이의 거리인 focal length와 cell의 크기 등 projection에 영향을 미치는 카메라 내부의 요인이고, extrinsic parameter는 카메라가 설치된 위치, 카메라가 바라보는 방향 등 카메라 외부의 요인이다.

간단한 예시를 들어보자. 카메라의 이미지 센서가 정사각형이고, focal length가 cell의 가로와 세로 방향 크기 각각 모두 $f$배이며, 주점은 이미지 센서의 cell array가 한쪽 방향으로 기울어지지 않았다고 하자. 또한 카메라 설치에 관해 rotation과 translation 모두 발생하지 않았다고 가정하자. 그러면 이미지 좌표계와 3차원 좌표계를 서로 변환할 수 있는 식은 위와 같이 구할 수 있다.

만약 카메라 설치에 관해 rotation과 translation이 바뀌어서 extrinsic parameter에 변화가 생기면 projection은 위의 사진처럼 식을 작성할 수 있다.

위의 예시에서는 3차원 현실 좌표계를 2차원으로 바꾸는 과정에 관해서만 설명이 되었지만, 2차원 이미지 좌표계를 3차원 현실 좌표계로 변하는 것도 간단히 구현 가능하다. Projection matrix의 역행렬을 양변에 곱해주면 3차원 이미지 좌표를 구할 수 있다.

NeRF 논문에서는 이러한 방법을 run_nerf_helpers 코드의 get_rays 함수를 사용하여 구현했다. Intrinsic parameter를 사용하여 direction에 관한 vector를 구하고, extrinsic parameter의 rotation에 해당되는 부분 행렬과 내적하여 rays_d를 계산했다. 또한 extrinsic parameter의 translation에 해당되는 벡터인 camera frame의 origin을 world coordinate으로 변환하여 ray origin인 rays_o를 구했다.

def get_rays(H, W, K, c2w):
    i, j = torch.meshgrid(torch.linspace(0, W-1, W), torch.linspace(0, H-1, H))
    i = i.t()
    j = j.t()

    dirs = torch.stack([(i-K[0][2])/K[0][0], -(j-K[1][2])/K[1][1], -torch.ones_like(i)], -1)
    rays_d = torch.sum(dirs[..., np.newaxis, :] * c2w[:3,:3], -1)
    rays_o = c2w[:3,-1].expand(rays_d.shape)
    return rays_o, rays_d

torch의 meshgrid를 이용해서 2차원 이미지의 $x$, $y$ 좌표 인덱스를 구하여 transpose하고, intrinsic parameter를 이용하여 dirs 벡터를 구한다. K[0][0]는 focal length가 $x$ 방향의 이미지 cell의 몇 배인지고, K[1][1]는 focal length가 $y$ 방향의 이미지 cell의 몇 배인 지며, K[0][0]과 K[1][1]은 camera frame origin의 $x$, $y$ 좌표이다. 실제로 ray는 3차원 상에 존재하므로 $z$ 원소 성분에 -1을 추가하여 stack을 통해 $x$, $y$, $z$ 성분에 관해 하나의 direction vector로 묶어주는 것으로 이해했다. 이를 extrinsic parameter인 c2w의 rotation 부분과 내적한 결과가 rays_d이다. rays_o에서는 c2w의 translation 부분을 camera frame의 origin으로 고려하여 이를 world coordinate으로 변환했다.

모델의 구조

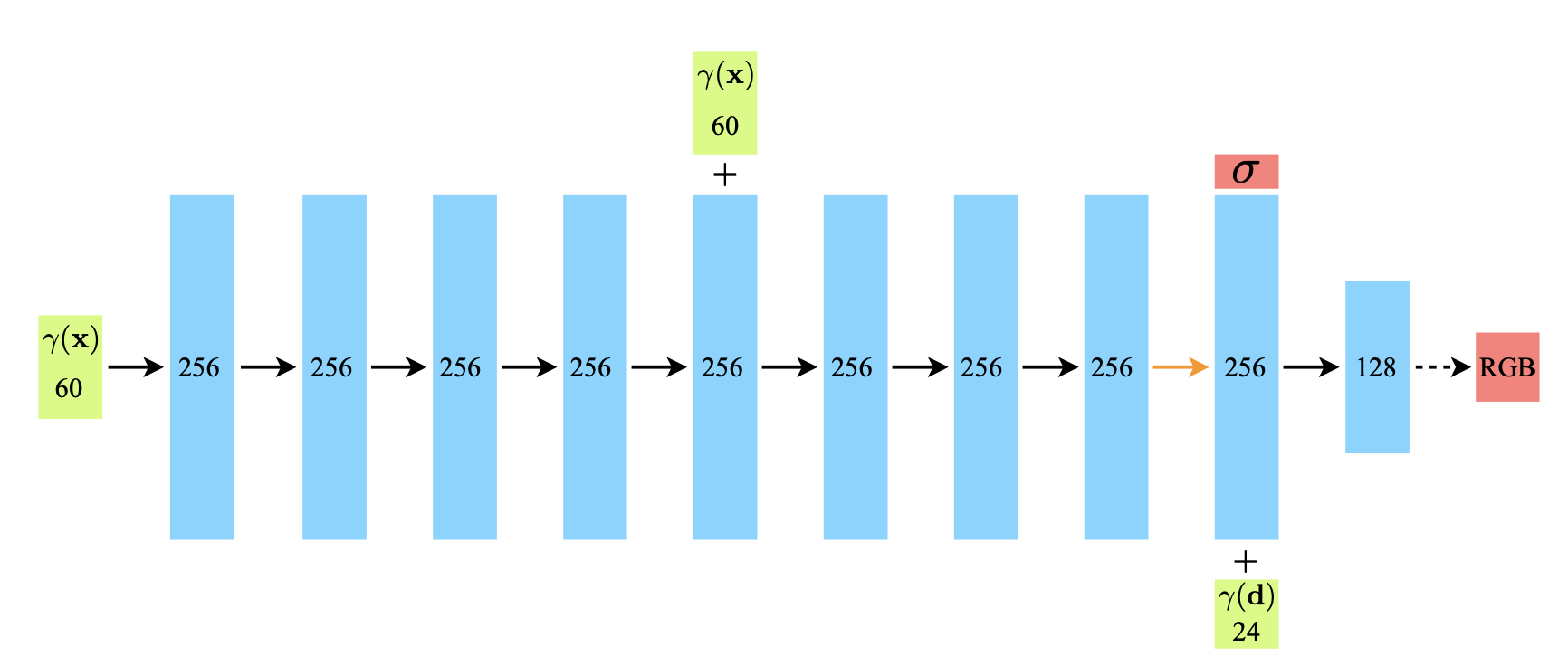
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Figure 7

NeRF의 neural network는 positional encoding된 point의 $(x, y, z)$ 좌표를 input으로 받아서 ReLU activation function을 사용한 8개의 fully connected layer를 통과시킨다. 이때, 각 레이어마다 채널은 256으로 유지시키고, 네 번째 layer에서 skip connection처럼 input을 한 번 더 concatenate 하여 받는다. 8번째 레이어까지 통과시키면 해당 point의 volume density와 256차원의 feature vector가 나온다. 여기서 viewing direction이 feature vector와 concatenate 되면서 또 하나의 layer를 통과하여 128차원으로 바꾼다. 이후 최종적으로 output layer를 통과시켜서 RGB 값인 output vector를 얻는다.

논문 구현 코드에서는 NeRF 클래스에 자세히 정의되어 있다. 모든 코드를 일일이 설명하기에는 내용이 길어질 것 같아서 중요한 부분 위주로 짚어보려고 한다.

# Append input channel to 4th layer.
# The model is composed of 8 layers.
# This model is used for learning volume density(sigma) and yielding a feature vector. 

self.pts_linears = nn.ModuleList(
    [nn.Linear(input_ch, W)] + 
    [nn.Linear(W, W) if i not in self.skips else nn.Linear(W + input_ch, W) for i in range(D-1)]
)

NeRF 클래스의 instance 초기화 함수에서 pts_linears 멤버 변수에 모델의 layer를 쌓아서 MLP를 구현한다. 이때 iterator가 skips 멤버 변수에 속하면 입력 크기를 더한 만큼의 채널 크기로 layer를 쌓는데, 여기서 default로 W는 채널의 크기인 256이고, skips는 [4]의 리스트로 온다. 그래서 저 위의 모델 구조도에서 4번째에 오는 레이어의 input으로 가장 처음에 들어왔던 좌표 input이 concatenate되는 과정을 구현한 것이다.

self.views_linears = nn.ModuleList([nn.Linear(input_ch_views + W, W//2)])

그 밑에 바로 오는 코드는 viewing direction을 input으로 받아 128 크기로 변환하는 레이어 모듈 리스트를 views_linears 멤버 변수에 하할당한 코드이다. 모델 그림과 연관 지어 보면 8번째 레이어 뒤에서 viewing direction을 input으로 받는 것과 대응되는 부분이다.

def forward(self, x):
    input_pts, input_views = torch.split(x, [self.input_ch, self.input_ch_views], dim=-1)
    h = input_pts

    for i, l in enumerate(self.pts_linears):
        h = self.pts_linears[i](h)
        h = F.relu(h)

        if i in self.skips:
            h = torch.cat([input_pts, h], -1)
    # At this time, an output(h) is a feature vector of data.

    # This is executed when you want to learn direction of view(d).
    if self.use_viewdirs:
        alpha = self.alpha_linear(h)
        feature = self.feature_linear(h)
        h = torch.cat([feature, input_views], -1)

        for i, l in enumerate(self.views_linears):
            h = self.views_linears[i](h)
            h = F.relu(h)

        rgb = self.rgb_linear(h)
        outputs = torch.cat([rgb, alpha], -1)
    else:
        outputs = self.output_linear(h)

    return outputs

NeRF의 neural network를 feed-forwarding 하는 부분인 forward 메소드를 살펴보면 모델의 학습 과정을 더 면밀하게 볼 수 있다. 처음에 8개의 layer에 관해서는 입력 데이터의 point의 volume density와 feature vector를 output으로 나오게 해야 한다. 이때, skips 리스트의 원소인 4번째 iteration의 layer에서는 input_pts와 h를 concatenate 한 input을 받아서 256차원의 output을 낸다.

use_view_dirs는 viewing direction 학습 여부를 의미한다. Viewing direction까지 학습하는 경우 volume density는 alpha에, feature vector는 feature에 받고, 앞서 쌓았던 views_linears 레이어 모듈 리스트를 통과하여 rgb 값을 output으로 받는다. Viewing direction을 학습하지 않는 경우에는 output_ch만큼의 크기를 지니도록 선형 레이어를 통과시켜서 outputs 결과를 얻는다. Viewing direction의 학습 여부에 따라 코드를 분기시킨 이유는 ablation study를 수행하기 위한 목적으로 추정된다.

왜 point의 density를 학습할 때는 viewing direction을 입력으로 사용하지 않을까?

어떤 위치의 밀도(density)는 외부 또는 내부 환경이 변화하지 않는 한 그대로 유지된다. 그러니까 우리가 어떠한 지점을 남동쪽에서 바라보는지 아니면 남서쪽에서 바라보는지 그 방향에 따라 해당 지점의 density는 변하지 않는다.

그러나 point의 색은 바라보는 방향에 따라 달라질 수 있다. 어떠한 방향에서 point를 바라볼 때는 해당 지점에 빛이 반사되어 더 밝게 보일 수 있고, 다른 방향에서는 빛이 비춰지지 않아 어둡게 보일 수 있다. 그래서 이 논문에서 저자는 point의 volume density인 $sigma$를 예측할 때는 위치 정보 $x$만을 사용하고, point의 RGB color인 $c$를 예측할 때는 위치 정보 $x$와 바라보는 방향인 $d$를 같이 input에 넣어 학습되도록 구현했다.

그런데 어떤 point의 volume density가 viewing direction에 의존적이지 않은 것은 맞지만, 그렇다고 viewing direction이 volme density를 학습하는 데 있어서 철저히 배제된다고 보기에는 어폐가 있다고 개인적으로 이해했다. NeRF에서는 여러 방향의 이미지에서 나오는 ray를 사용하는데, 이 ray들의 교점이 point로 샘플링되었다고 하자. 만약에 한 ray에서 point를 본 색이 초록색이고 다른 ray에서 그 point를 본 색은 빨간색이라고 하자. 그러면 바라보는 방향에 따라 그 point의 색이 변했다는 의미이므로, 해당 point의 밀도는 매우 낮아서 투명하여 그 point 뒤에 있는 색이 보였다고 해석할 수 있다. 만약에 해당 point의 밀도가 높았다면 그 지점의 색이 큰 변화 없이 나올 가능성이 높기 때문이다. (물론 방향에 따라 빛의 영향이 달라지는 것도 배제할 수는 없다.) 그래서 여러 방향에서 MLP를 학습했을 때 색상의 변화가 크게 생기지 않았다면 해당 지점의 density는 높다고 해석할 수 있고, 색상의 변화가 크다면 density가 낮아서 그 지점 뒤에 있는 공간의 색이 보일 가능성이 높다고 볼 수 있다.

즉, NeRF에서 MLP가 하나의 point를 여러 viewing direction에서 바라 본 데이터를 고려하여 volume density를 학습하는 것은 맞지만, volume density를 학습할 때 여러 viewing direction에 관한 데이터가 직접 함수의 input으로 들어가지는 않는다고 이해하는 것이 더 낫지 않을까 싶다. 다시 말해, 하나의 point에 관해 여러 viewing direction에서 volume density와 color를 학습할 때 동일한 모델의 파라미터를 가지고 학습을 수행하므로, 모델이 여러 viewing direction에서 하나의 point를 본 데이터를 학습하는 것 자체는 틀린 말이라고 보기 어렵다고 개인적으로 이해했다. (틀린 해석일 수 있으므로 지적 또는 반박 언제든지 댓글로 남겨주시면 감사하겠습니다.)

일반적인 딥 러닝 모델처럼 이해하면 곤란하다

딥 러닝 또는 머신러닝을 사용할 때는 학습 데이터를 가지고 모델의 파라미터를 학습한 후, 학습에 사용되지 않은 unseen data에 관해 모델이 예측을 수행하여 모델의 일반화 성능이 어떤지를 고려하는 경우가 흔하다. Classification, segmentation task 등 주로 학습이 되지 않은 새로운 데이터에 관해 모델이 얼마나 좋은 성능을 보이는지를 평가한다. 그러나 이 논문에서 neural network를 사용한 목적은 이와 거리가 있다. 여기서는 한 이미지에 관해 3D 정보를 잘 학습하여 novel view를 잘 생성할 수 있도록 하나의 이미지에 관해서만 overfitting을 수행하는 목적으로 neural network를 사용하는 것이다. 다시 말해, 머신러닝을 어디까지나 '도구'로 사용한 것으로 이해하는 게 바람직하다.

개인적으로 NeRF의 neural network가 학습한 파라미터를 단순히 하나의 이미지에 overfitting 하는데 국한시키는 것에서 벗어나 다양한 새로운 이미지에 관해서도 뭔가 예측을 하는 task를 수행하는 데 써먹을 수 있지 않을까 하는 의문이 들었다. 이렇게 기학습된 parameter를 가지고 다른 task에 활용하는 논문들도 NeRF 이후에 제안되었다는데, 이 글에서는 거기까지는 정리하지 않으려고 한다. 추후 이에 관해 공부해보고자 한다.

Positional Encoding

논문에서는 앞서 설명한 바와 달리 $xyz\theta\phi$의 input coordinate의 데이터를 바로 입력으로 넣지 않고 positional encoding을 통해 입력을 좀 더 고차원으로 보내서 neural network가 high frequency variation 데이터에 더 잘 적합될 수 있도록 했다고 말한다. Positional encoding을 사용한 이유는 단순히 원래 input coordinate을 입력으로 네트워크에 넣어서 학습하면 high frequency variation을 표현하는 데 좋지 않은 성능을 보여서라 한다. 여기서의 poistional encoding은 'Attention is All You Need' 논문의 transformer에서 사용된 것과는 다른 목적으로 사용된다. Transformer에서는 self-attention을 수행할 때 병렬적으로 token을 입력으로 받으므로 token에다가 $\sin$, $\cos$ 등 함숫값을 더하여 token에 순서에 관한 정보를 부여했다. Transformer의 positional encoding과 관련한 내용은 아래 글을 참조하면 된다.

https://glanceyes.tistory.com/entry/Transformer의-Multi-Head-Attention과-Transformer에서-쓰인-다양한-기법

Transformer의 Multi-Head Attention과 Transformer에서 쓰인 다양한 기법

들어가기 전에 앞서 우리는 입력으로 주어진 sequence에서 어떠한 부분에 주목할지를 예측에 반영하는 attention 기법을 배웠다. 이러한 Self-Attention에서 좀 더 나아가 head를 여러 개 사용하여 주어진

glanceyes.com

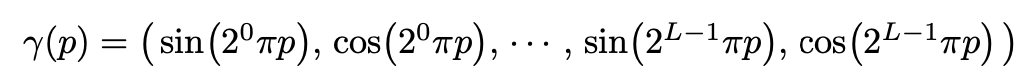
그래서 저자는 기존의 네트워크 $F_{\theta}$를 두 개의 함수 $F_{\theta}'$와 $\gamma$로 구성하여 만들었다. 여기서 $\gamma$는 $\mathbb{R}$을 $\mathbb{R}^{2L}$로 mapping 하는 함수이다. 개인적으로 이 부분을 SVM(Support Vector Machine)에서 커널 함수를 통해 저차원의 데이터를 고차원으로 변환하여 학습하는 것과 어느 정도 비슷한 맥락을 보인다고 이해했다.

# Positional encoding
class Embedder:
    def __init__(self, **kwargs):
        self.kwargs = kwargs
        self.create_embedding_fn()

    def create_embedding_fn(self):
        embed_fns = [] # embedding functions
        d = self.kwargs['input_dims']
        out_dim = 0
        
        # whether include input or not
        if self.kwargs['include_input']:
            embed_fns.append(lambda x: x)
            out_dim += d

        max_freq = self.kwargs['max_freq_log2']
        N_freqs = self.kwargs['num_freqs']

        if self.kwargs['log_sampling']:
            freq_bands = 2.**torch.linspace(0., max_freq, steps=N_freqs)
        else:
            freq_bands = torch.linspace(2.**0., 2.**max_freq, steps=N_freqs)


        for freq in freq_bands:
            # p_fn is a function such as sine or cosine.
            for p_fn in self.kwargs['periodic_fns']:
                embed_fns.append(lambda x, p_fn=p_fn, freq=freq : p_fn(x * freq))
                out_dim += d

        self.embed_fns = embed_fns
        self.out_dim = out_dim

    def embed(self, inputs):
        return torch.cat([fn(inputs) for fn in self.embed_fns], -1)

실제 코드에서는 run_nerf_helpers.py 파일의 Embedder라는 클래스에서 구현되어 있다. 간단히 살펴보면 클래스의 인스턴스가 생성될 때 create_embedding_fn 함수가 호출되고, 그 함수에서 0과 max_feq 사이에서 점들을 샘플링하여 이를 kwargs['periodic_fns']의 각 함수별로 샘플링한 값을 곱하는 lambda 함수를 embed_fns에 넣는다. 이때 kwargs['periodic_fns']는 default로 sin, cos이 들어간다.

Volumetric rendering은 무엇인가?

앞에서 본 neural network는 3차원 상에서 ray 위의 어떤 단일 지점(point)에 관한 volume density와 color를 학습하고 예측하는데 사용되었다면, volumetric rendering에서는 ray 위에 존재하는 샘플링된 여러 개의 point에 관한 volume density와 color를 사용하여 그 ray가 들어오는 2D 이미지의 최종적인 픽셀에서 어떠한 색으로 보일 지를 구하는 과정이다.

이 논문에서 volumetric rendering function은 새로운 내용을 발견하거나 떠올려서 정의한 것은 아니고, 기존에 사용하던 volume rendering 방식을 그대로 응용하여 가져온 것이다. 앞서 우리는 2D 이미지의 한 픽셀에서 나가는 ray 위의 각각 하나의 점(point)들에 관해 volume density와 color를 구했다. 이를 가지고 그 픽셀에 ray가 들어올 때 최종적으로 어떠한 색과 투명도를 보일 지를 결정하는 것이 바로 volumetric rendering이다. 이 부분을 neural network에서 학습하고자 하는 내용과 혼동하지 말아야 한다.

식을 그대로 완벽히 외우기보다는 식에 내재된 직관을 파악하는 것이 중요하다고 생각했다. 먼저 이 모델에서 volumetric rendering을 위한 volumetric rendering equation 식이 어떻게 정의되었는지를 이해하기 전에 그 식을 구성하는 각각의 기호가 무엇을 뜻하는지를 살펴보자.

$\mathbf{r}$: ray의 color
$\mathbf{r}(t)$: ray 위에 있는 point
$t_n$: lower bound로서 가장 가까운 point
$t_f$: upper bound로서 가장 먼 point
$T(t)$: point가 있는 위치 앞까지 얼마나 광선이 부딪히지 않고 통과하는지(광선이 $t$까지 얼마만큼 도달했는지 그 비율)
$\sigma(\mathbf{r}(t))$: point가 있는 위치의 밀도가 얼마인지(point의 volume density)
$\mathbf{c}(\mathbf{r}(t), \mathbf{d})$: viewing direction에서 볼 때 point의 color
$C(\mathbf{r})$: ray의 color

우리가 임의의 pixel에 도달하는 광선 ray $\mathbf{r}$를 하나 정했으면, 그 ray에서 lower bound와 upper bound 내의 범위에서 일부 point들을 샘플링한다. 그 샘플링된 포인트를 $\mathbf{r}(t)$라고 하면, 앞서 설명한 neural network에 의해 $\mathbf{r}(t)$의 volume density인 $\sigma(\mathbf{r}(t))$와 color인 $\mathbf{c}(\mathbf{r}(t), \mathbf{d})$을 구한다. 이를 모든 샘플링한 point들에 관해 구하여 위의 식에서 integral 해주면 광선 $\mathbf{r}$이 픽셀에 보이는 color가 정해지는 것이다.

이때 $T(t)$는 point $\mathbf{r}(t)$가 있는 위치 앞까지 얼마나 광선이 부딪히지 않고 통과하는지 그 transmittance를 사용을 한다. 이 항은 ray 위의 lower bound부터 $t$까지 범위에 속한 point들의 volume density를 모두 적분한 값에 음수를 취하여 exponential을 씌운 결과인데, exponential 함수에서 지수가 음수이면 지수의 절댓값이 증가할 때 함숫값은 작아진다. 그러므로 적분한 volume density 값이 커지면 transmittance 값이 작아지는 것을 의미하며, 이는 앞쪽에 volume density가 높은 point들을 많이 지나면서 그 뒤로부터 통과하는 ray 비율이 낮아진다고 해석할 수 있다.

이 volumetric rendering을 통해 구한 color와 실제 사진의 color의 loss를 구하고 이 loss를 줄이는 방향으로 최적화하는 것이 이 방법의 핵심이다.

Volumetric rendering을 위한 입력 샘플링

이미지의 모든 ray를 한번에 학습하는가?

이미지의 모든 픽셀에 관해 뻗어가는 ray를 모두 학습시키는 건 현실적으로 어렵다. 예를 들어 $500 \times 500$ 크기의 이미지에서 나오는 모든 ray를 학습하려면 250,000개의 ray가 학습 대상이 된다. 하나의 ray에 관해서도 그 ray 위의 point들을 학습해야 하는데, ray의 수부터가 많아지면 하나의 이미지에 관해 학습할 때 OOM(Out Of Memory) 문제가 발생할 수 있다. 그래서 이 논문에서는 4,096개 샘플 포인트를 하나의 단위로 chunking하여 GPU에 올려서 이미지 rendering을 학습한다.

하나의 ray 위에 존재하는 모든 point를 다 학습하는가?

아니다. 현실적으로 discretized voxel grids가 아닌 이상 continuous 공간에서 한 직선 위의 모든 점들에 관해 volumetric rendering 시 continuous integral을 수행하는 것은 쉽지 않다. 그래서 논문에서는 구적법(quadrature)으로 continuous integral에 근사하는 방법을 택했다.

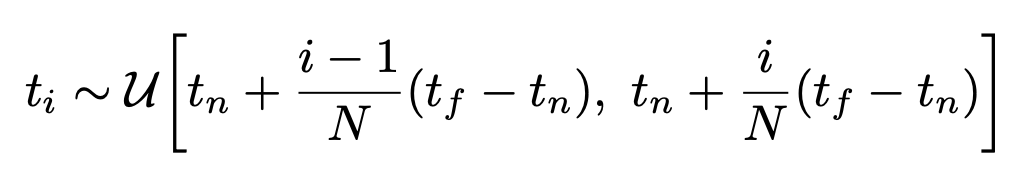
그러나 단순히 구적법으로 적분할 때 쓰이는 값의 개수가 제한되어 있어서 고정된 discrete location의 point set만 뽑을 가능성이 있다. 그래서 논문에서는 stratified sampling 접근법을 사용하여 ray의 범위를 균등한 spaced-bin으로 나누고, 그 bin에서 랜덤하게 point를 sampling 했다.

Stratified sampling을 통해 재정의한 volumetric rendering function

이렇게 stratified sampling을 적용하여 volumetric rendering을 하는 식을 위처럼 재정의했다. 여기서 저자는 $\hat{C}(\mathbf{r})$를 coarse network로 말하는데, 이후 나올 hierarchical volume sampling을 위해 사용된다. 또한, $\delta_j$는 $j$번째 point와 $j + 1$번째 point 사이의 거리처럼 인접한 샘플들 사이의 거리를 뜻한다.

Hierarchical Volume Sampling

저자는 위의 stratified sampling 방식이 비효율적이라고 하는데, 왜냐면 만약 공기처럼 밀도가 낮은 free space나 ray의 앞에서 어떠한 물체에 의해 가려진 occluded region에서 point가 뽑히게 되면 pixel의 색에 영향을 끼치지 않는다. 그래서 volume density가 높은 공간에서 point들을 많이 sampling 하면 ray의 색을 결정짓는데 더 영향을 끼치는 point들을 더 많이 뽑을 수 있다는 아이디어다. 즉, hierarchical volume sampling을 통해 neural network에서 학습하는 마지막 렌더링에서 예측되는 효과에 비례하여 점들을 샘플링한다면 렌더링 효율을 더 높일 수 있다는 것이다.

그래서 저자는 coarse와 fine이라는 두 개의 network를 동시에 최적화하는 방법을 택했다. 먼저 coarse network는 앞서 설명한 stratified sampling으로 point를 샘플링하고 volumetric rendering function을 최적화한다. 이 coarse network의 output이 ray의 일차적인 색인 $\hat{C}_c(\mathbf{r})$도 알려주지만, 이 과정에서 각 point별로 구한 transmittance와 volume density를 가지고 ray 위의 점에서 어떠한 부분이 더 ray의 색에 영향을 많이 끼치는지 그 가중치 $w_i$도 구할 수 있으며 이를 바탕으로 다시 샘플링을 수행한다. 여기서 왜 가중치의 개념이 나오는지 궁금하다면 아래 그림을 같이 보면서 이해하면 좋다.

구체적으로 그 과정에 관해 설명하면 weight $w_i$를 정규화하여 piecewise-constant PDF(Probability Density Function)을 구하고, 이 분포로부터 다시 point를 샘플링한다. 코드에서는 PDF를 CDF(Cumulative Distribution Function)으로 바꿔서 샘플링하는 방법으로 구현했다. 그리고 여기서 가중치 $w_i$는 transmittance인 $T_i$와 $(1 - \exp(-\sigma_i \delta_i))$를 곱한 값이다. 한 point 앞으로 더 많은 비율의 ray가 도달하면 그 point 앞까지의 transmittance가 높은 것이고, 그 point의 밀도가 높으면 높을수록 해당 point의 색이 ray의 색에 영향을 더 많이 끼치게 되므로 가중치를 transimttance와 volume density의 곱으로 설정한 것이다. 즉, 앞쪽에 빛이 통과하는 데 걸리적거리는 게 없어서 ray가 point 앞까지 많이 통과해 오고, 게다가 그 지점(point)의 밀도가 높으면 그 점이 ray의 색에 더 많이 영향을 끼치므로 샘플링될 확률과 비례하게 가중치를 높게 주는 것이다.

이렇게 coarse network에서 사용한 sampling 점들인 $N_c$와 fine network에서 다시 샘플링할 때 뽑은 점들인 $N_f$를 가지고 최종적인 컬러인 $\hat{C}_f(\mathbf{r})$를 렌더링 할 때 사용한다.

최종적으로 NeRF는 batch 내에 속하는 ray에 관해 coarse network로 예측한 렌더링 색과 ground truth 간의 L2 norm, fine network로 예측한 렌더링 색과 ground truth 간의 L2 norm의 합을 loss로 정의하고, 이를 최소화하는 방향으로 학습한다.

NeRF를 jupyter notebook으로 간단하게 코드로 구현한 실습 파일은 아래를 참고하면 된다.

GitHub - Glanceyes/ML-Paper-Review: Implementation of ML&DL models in machine learning that I have studied and written source co

Implementation of ML&DL models in machine learning that I have studied and written source code myself - GitHub - Glanceyes/ML-Paper-Review: Implementation of ML&DL models in machine learnin...