Neural Tangent Kernel과 Fourier Features를 사용한 Positional Encoding (3) - Fourier Features
- -
이 글 시리즈는 'Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains' 논문과 이를 이해하는 데 필요한 선수 내용을 소개한 'Neural Tangent Kernel: Convergence and Generalization in Neural Networks' 논문을 기반으로 한다. 하나의 글로 작성하면 내용이 너무 길어질 것 같아서 '(1) Kernel Method', '(2) Neural Tangent Kernel', 그리고 '(3) Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains'의 세 부분으로 나눠서 작성하고자 한다. 이 글은 (2)을 설명한 지난 글에 이어 (3)에 관한 내용을 작성하고자 한다.
Neural Tangent Kernel에 관해 설명하기 전에 kernel의 정의와 kernel method에 관해 궁금하면 지난 글을 참고하면 된다.
(1) Kernel Method
Neural Tangent Kernel과 Fourier Features를 사용한 Positional Encoding (1) - Kernel Method
Positional encoding은 AI 모델링 분야에서 많이 쓰이는 기법 중 하나이다. 대표적으로 transformer에서도 데이터를 병렬 처리하여 학습하는 단점을 보완하여 데이터를 구성하는 각 token에 위치 정보를 부
glanceyes.com
(2) Neural Tangent Kernel
Neural Tangent Kernel과 Fourier Features를 사용한 Positional Encoding (2) - Neural Tangent Kernel
이 글 시리즈는 'Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains' 논문과 이를 이해하는 데 필요한 선수 내용을 소개한 'Neural Tangent Kernel: Convergence and Generalization in Neural Networks'
glanceyes.com
Neural Tangent Kernel
이전 글에서 NTK(Neural Tangent Kernel)을 분석하면서 왜 infinite-width network에서 모델의 파라미터가 데이터에 잘 맞게 수렴할 수 있는지를 보였다. 그런데 이제 NTK의 positive definite한 특성을 확인하면서 모델이 학습할 때 왜 high frequency에 관한 데이터에는 잘 집중하지 못하는지를 알아보고자 한다.
NTK와 Gram Matrix

NTK도 결국 지난 글에서 설명한 바처럼 kernel이다. Kernel은 각각의 데이터 쌍에 관한 유사도를 구한 결과로 이해할 수 있는데, NTK에서는 두 데이터에 관하여 각각의 gradient의 내적을 element로 지니는 행렬로 해석할 수 있다. 그래서 NTK는 gram matrix의 일종으로 볼 수 있다.
Gram matrix는 ML에서 자주 나오는 개념인데, 두 데이터 또는 두 채널 간의 관계가 어떻게 되는지를 통계적으로 보여주는 행렬이라고 볼 수 있다. 보통 분포의 개념과 연관지으면 공분산으로도 해석할 수도 있으며, computer vision에서는 channel 간의 분포가 얼마나 유사한지를 보여주고, 추천 시스템에서는 아이템 간의 유사도를 보여주는 목적으로도 사용한다고 알고 있다.
그런데 Gram matrix는 항상 positivie semidefinite 하다는 특성을 지니고 있다. 여기서 positive semidefinite는 어떠한 linear transformation matrix
어떤 행렬이 positive semidefinite이면, 그 행렬의 모든 eigenvalue의 값은 0보다 크거나 같다. 이는 다음과 같이 증명할 수 있다.
여기서
NTK와 Positive Definite

그런데 Gram matrix에 해당되는 NTK는 positive semeidefinite이 아니라 항상 positive definite 하다는 특성을 지니고 있다. 여기서 positive definite의 정의를 써 보면 아래와 같다.
어떤 matrix가 positive definite 하면 그 matrix의 eigenvalue는 항상 0보다 크다. 이에 관한 증명은 앞서 설명한 positive semidefinite에서의 증명과 같다.
그런데 infinite-width를 지닌 네트워크에서의 NTK가 positive definite 하다는 건 어떻게 직관적으로 이해할 수 있을지 개인적으로 궁금했다. 이는 모든 NTK를 gradient에 관한 gram matrix와 activation function으로 표현 가능하다는 사실에서 도출할 수 있다. 예시를 들자면, 지난 글에서 1개의 hidden layer를 지니면서 어떤 한infinite-width neural network에서의 NTK를 구한 적이 있다.
앞서 Gram matrix인 kernel은 positive semidefinte 하다고 했는데, 위의 식을 보면 모든 positive semidefinite matrix의 expectation도 positive semidefinite 하다. 그리고 만약에 activation function

이 neural network는 infinite-width를 지니고 있다고 가정했는데, neural network의 너비가 충분히 크다는 건 그만큼 파라미터들이 네트워크에 많이 있다는 것을 뜻한다. 그러므로 일부 파라미터의 값이 변화하는 것만으로는 네트워크 전체에 큰 영향을 미치지 못한다고 볼 수 있다. 그런데 그 수많은 파라미터에 관하여 ReLU의 미분값이 0인 경우는 불가능에 가까우므로 integration해서 expectation을 구하면 웬만해서 0보다는 클 것이라고 예상할 수 있다. 그래서 직관적으로 infinite-width network에서는 NTK가 positive definite이다. 이는 activation function 종류 또는 데이터의 분포에 관계없이 성립한다고 알려져 있다.
NTK와 Eigenvalue Spectrum

즉, NTK가 poistive definite이므로 이 NTK의 eigenvector의 eigenvalue는 0보다 크다는 사실을 얻게 된다. 그러면 지난 글에서 infinite-width network의 error가 어떻게 수렴하는지를 보였던 식인
그러면 앞서 정의한 error가 어떻게 수렴하는지를 보인 식을 위와 같이 정리할 수 있다. 그러면 NTK의 eigenvalue가 convergence rate에 관여한다는 사실을 확인할 수 있다. 예를 들어,
그런데 잠시 신호처리의 내용을 빌려서, eigenvector

여기서 주목해야 할 점이 있는데, 일반적인 데이터의 분포를 살펴보면 frequency가 낮은 데이터의 eigenvalue는 높은 intensity를 지니고 있는 반면에, frequency가 높은 데이터의 eigenvalue는 낮은 intensity를 지니고 있다. 이에 관해서 직관적으로 이해해 보자면, frequency가 낮은 영역에 대응되는 데이터는 상대적으로 coarse한 정보를 지니고 있고, frequency가 높은 영역에 대응되는 데이터는 상대적으로 noise에 가까운 fine한 정보를 지니고 있다. 그런데 일반적인 데이터는 주로 noise보다는 전반적인 영역에 관한 정보가 좀 더 강하게 반영되어 있음을 예상할 수 있다. 이는 noise의 intensity가 높은 데이터의 분포가 그리 흔하지는 않는다는 상식과 연결된다. 다시 말해, frequency가 낮은 영역에서는 높은 intensity에 대응되는 큰 fourier basis coefficient를 지니고 있는데, 이것이 eigenvalue로 볼 수 있으므로 큰 eigenvalue를 지니고 있다. 그런데 eigenvalue가 크면 네트워크의 error가 eigenvalue에 대응되는 eigenvector 방향으로 빠르게 수렴한다고 했다. 그래서 infinite-width network에서는 일반적인 데이터에 관해 frequency가 낮은 영역에 대하여 더 빠르게 수렴한다는 것이다.
정리하면,
그래서 기존에는 infinite-width neural network가 coarse한 정보에만 집중했지만, Fourier feature로 high frequency 영역의 intensity를 높임으로써 더 fine한 정보에도 집중할 수 있다는 것이다. 여기서 intensity는 그 주파수의 진폭으로 이해해도 좋다.
논문에서는 error에 관한 eigenvalue spectrum에 관해 좀 더 복잡하게 정리를 했는데, 이 글에서는 엄밀한 수학적 증명보다는 직관을 이해하는 게 바람직하다고 느껴서 NTK에 관한 내용은 여기서 마치려고 한다.
Fourier Feature
이 논문의 핵심을 짧게 요약해서 말하자면, nerual network에 주어지는 저차원의 input에 다양한 주파수와 진폭을 지니는 sinusoidal 함수를 적용하여 좀 더 고차원으로 보낸 결과를 input으로 만들어서 network에 넣었을 때 기존보다 좀 더 고차원의 정보를 잘 학습할 수 있다는 것이다. 앞서 설명한 바처럼 network를 학습하는 데 NTK가 관여를 하고, training error를 줄이는 과정에서 데이터의 주파수(eigenvector)의 진폭(eigenvalue)이 커지면 커질수록 그 주파수에 대응되는 데이터의 error 수렴 방향이 더 빠르다는 점을 확인했다. 그런데 일반적인 데이터의 분포를 살펴보면 대체로 낮은 주파수에 대응되는 coarse한 정보의 intensity가 noise와 연관된 높은 주파수에 대응되는 fine한 정보보다 더 높다고 한다. 그래서 대개 network가 coarse한 정보는 빠르게 학습하는 반면에, fine한 정보는 느리거나 잘 학습하지 않는다. 그런데 Fourier feature를 사용하여 앞서 설명한 데이터의 양상에 좀 변화를 시켜주는, 다시 말해 높은 주파수의 진폭을 증가시킴으로써 fine 정보도 좀 더 잘 학습할 수 있게끔 했다는 것이 바로 이 Fourier feature의 핵심이다. 이러한 개념을 미리 생각하고 이 논문을 읽으면 구체적인 내용도 어렵지 않게 이해할 수 있었다.
Contribution
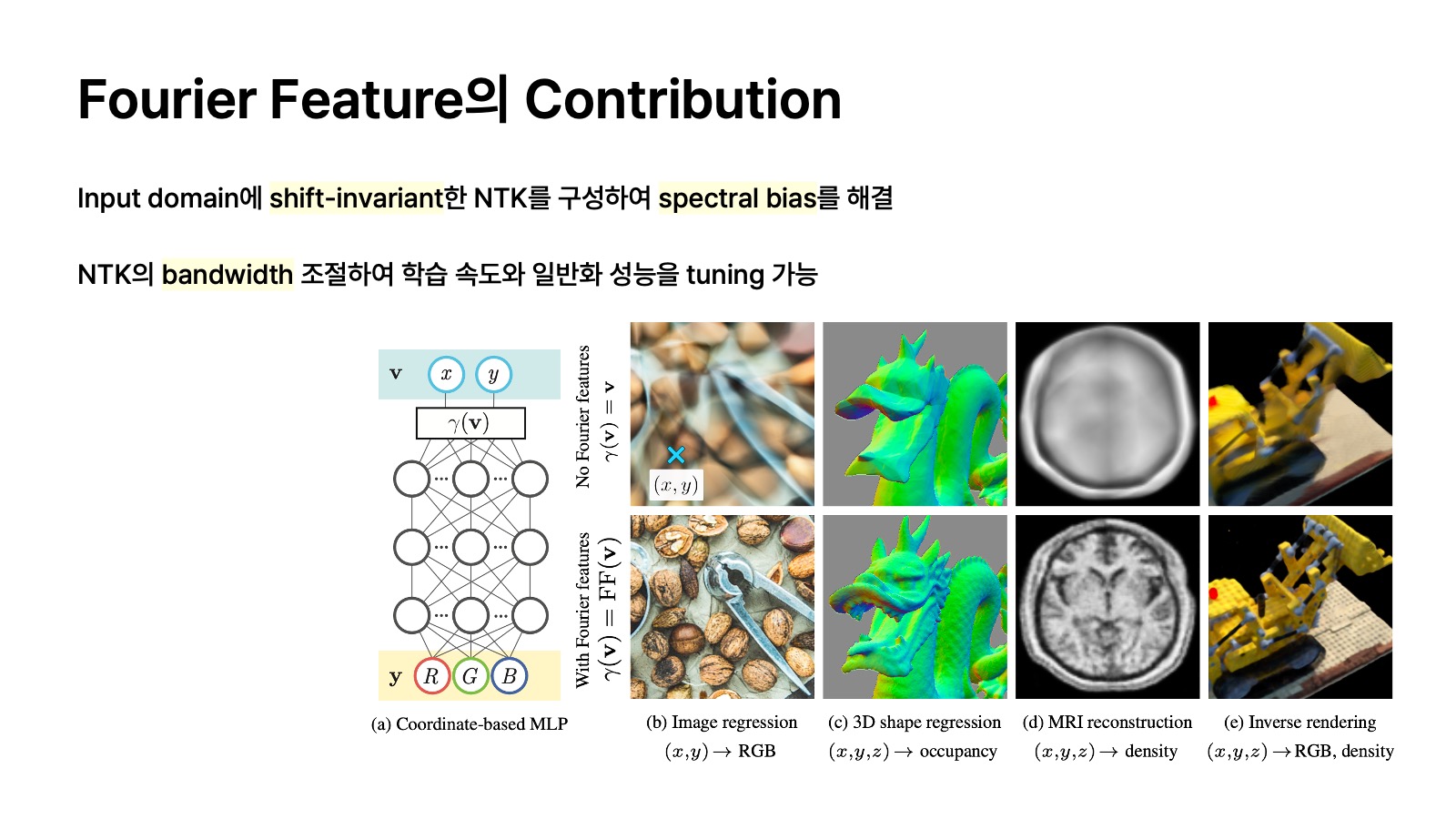
이 논문의 contribution을 말하자면 두 가지로 요약할 수 있다.
1. Input domain에 shift-invariant한 NTK를 구성하여 spectral bias를 해결했다.
2. NTK의 bandwidth를 조절하여 학습 속도와 일반화 성능을 tuning 할 수 있다.
첫 번째에서 shift-invariant 하다는 건, 이미지가 조금 이동되었거나 하더라도 이에 영향을 받지 않고 두 input point의 차이에만 의존한다는 특성인데, 이는 뒤에서 NTK의 kernel function을 분석하면 자세히 알 수 있는 내용이다. Spectral bias는 앞서 설명한 바처럼 sufficiently large width를 지닌 neural network가 high frequency를 잘 학습하지 못하는 특성을 나타낸다.
두 번째는 NTK도 결국 kernel인데, kernel regression을 수행하는 과정에서 bandwidth가 중요하다. 일반적으로 network에서 NTK의 bandwidth를 조절하는 것은 어려운데, Fourier feature를 사용하면 kernel의 bandwidth에 대한 control이 쉬워진다. 이도 뒤에서 kernel function 식을 정리하면서 알아볼 예정이다.
Fourier Feature와 Positional Encoding

Positional encoding은 'Attention is All You Need' 논문에서 제안된 input의 각 token 마다 여러 주파수와 진폭을 갖는 sinusoidal 함수의 합으로 mapping 하여 위치 정보를 부여하는 방법으로 유명하다. Fourier feature에서의 positional encoding도 다양한 주파수와 진폭을 지닌 sinusoidal 함수의 합으로 input을 mapping 하는 건 동일하다. 그런데 여기서의 목적은 위치 정보를 부여하는 게 아니라 앞서 말한 spectral bias, 다시 말해 높은 주파수의 정보를 제대로 학습하지 못하는 현상을 해결하기 위한 용도이다.
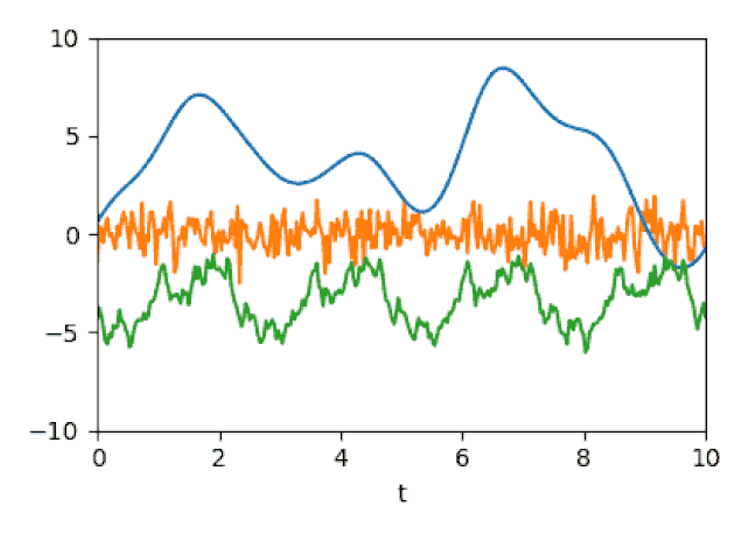
여기서는 Fourier transformation의 개념과 연관지을 수 있다. Fourier transformation은 시간에 따라 변하는 임의의 데이터를 여러 주파수와 진폭을 지닌 sinusoidal 함수의 합으로 나타내는 변환이다. 이 여러 주파수의 sinusoidal 함수 요소들이 Fourier basis를 구성한다고 볼 수 있고, 그 진폭이 basis를 구성하는 요소들의 coefficient로 볼 수 있다. 물론 이 basis function들의 선형 결합으로 나타내서 이전의 원래 데이터로 완전히 복원하지는 못한다. 여하튼 이처럼 input을 다양한 주파수와 진폭의 sinusoidal 함수에 넣어서 이들의 합으로 나타내어 input 데이터를 좀 더 고차원으로 보내는 작업이 바로 positional encoding이다.
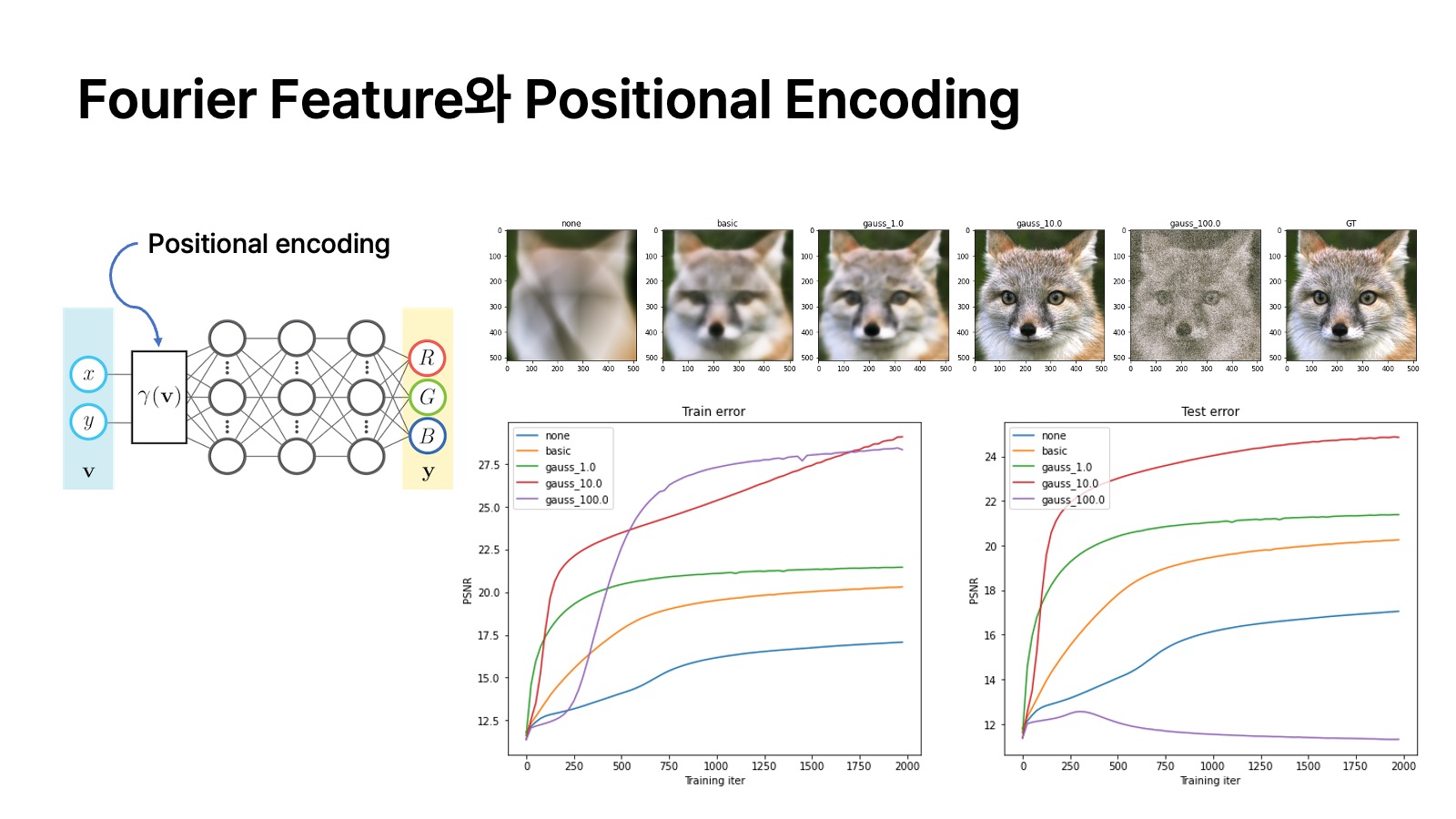
위의 그림은 2D 이미지가 주어졌을 때 모든 픽셀을 학습 데이터와 테스트 데이터로 일정 비율로 나누고. 테스트 데이터에 속하는 픽셀의 RGB 값은 지운다. 학습 데이터 set에 속하는 pixel의 2차원 좌표인
그림의 왼쪽은 네트워크의 앞단에 input
NTK와 Kernel Regression

앞서 NTK로 network의 파라미터를 학습하는 과정은 kernel regression과 유사하다고 정리했다. 그런데 여기서 어떤 데이터 포인트
Kernel의 Bandwidth
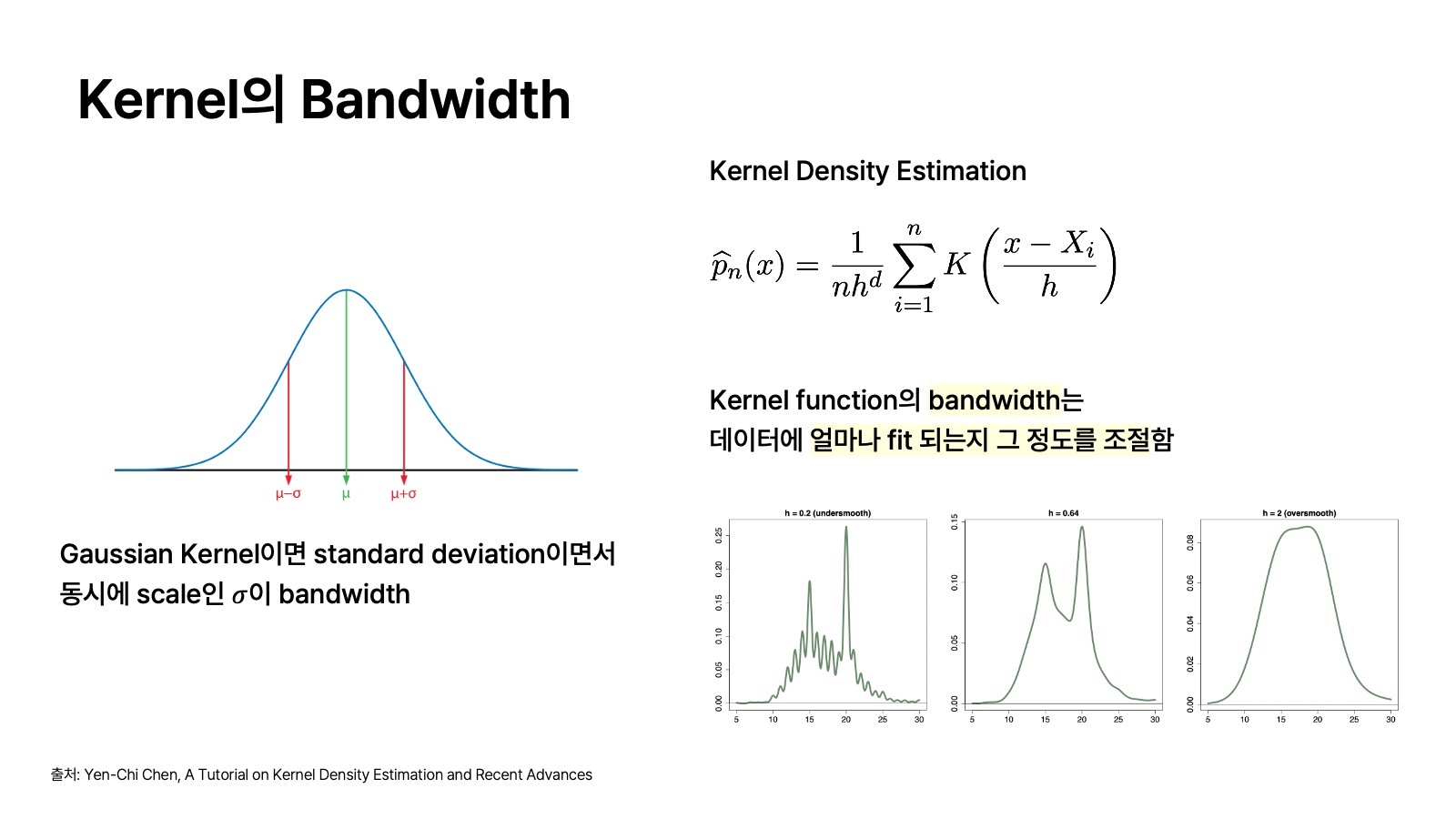
이 kernel의 bandwidth가 가중합으로서의 조절에 영향을 미치는데, 이는 kernel density estimation을 통해 이해해 볼 수 있다. Kernel density estimation에서는 kernel의 bandwitdth에 해당되는
위의 그림에서 왼쪽 위의 정규분포 그래프를 확인해 보자. 만약에 kernel이 gaussian kernel이라고 가정하면 그 gaussian 분포의 standard deviation이면서 동시에 scale이라고 불리는
오른쪽 아래 그래프는 kernel function의 bandwidth가 데이터에 얼마나 fit이 잘 될 수 있는지 그 정도를 조절하는 데 역할을 한다는 사실을 보여준다. Kernel의 bandwidth 사이즈가 너무 작으면 overfitting 되는 현상을 보이고, bandwidth 사이즈가 너무 크면 overfitting 되는 현상을 보이게 된다. 그래서 kernel의 적합한 bandwidth를 잘 찾는 것이 중요하다.

그래서 모델을 잘 학습시키기 위해서는 그 network 모델의 NTK의 bandwidth를 조절해서 적합한 값을 찾는 것이 중요하다. 그런데 기존의 neural network 상에서는 NTK의 bandwidth를 explicit 하게 조절하기가 어렵다. 그래서 Fourier feature를 통해 이러한 bandwidth를 explicit 하게 조절할 수 있도록 하는 것이다. Fourier feature에서는 그 주파수

앞서 여우 이미지에 관한 같은 실험을 다른 사진을 대상으로 진행했을 때 결과를 나타낸 것이다. 이 실험에서는 대신 주파수
Fourier Feature의 방법
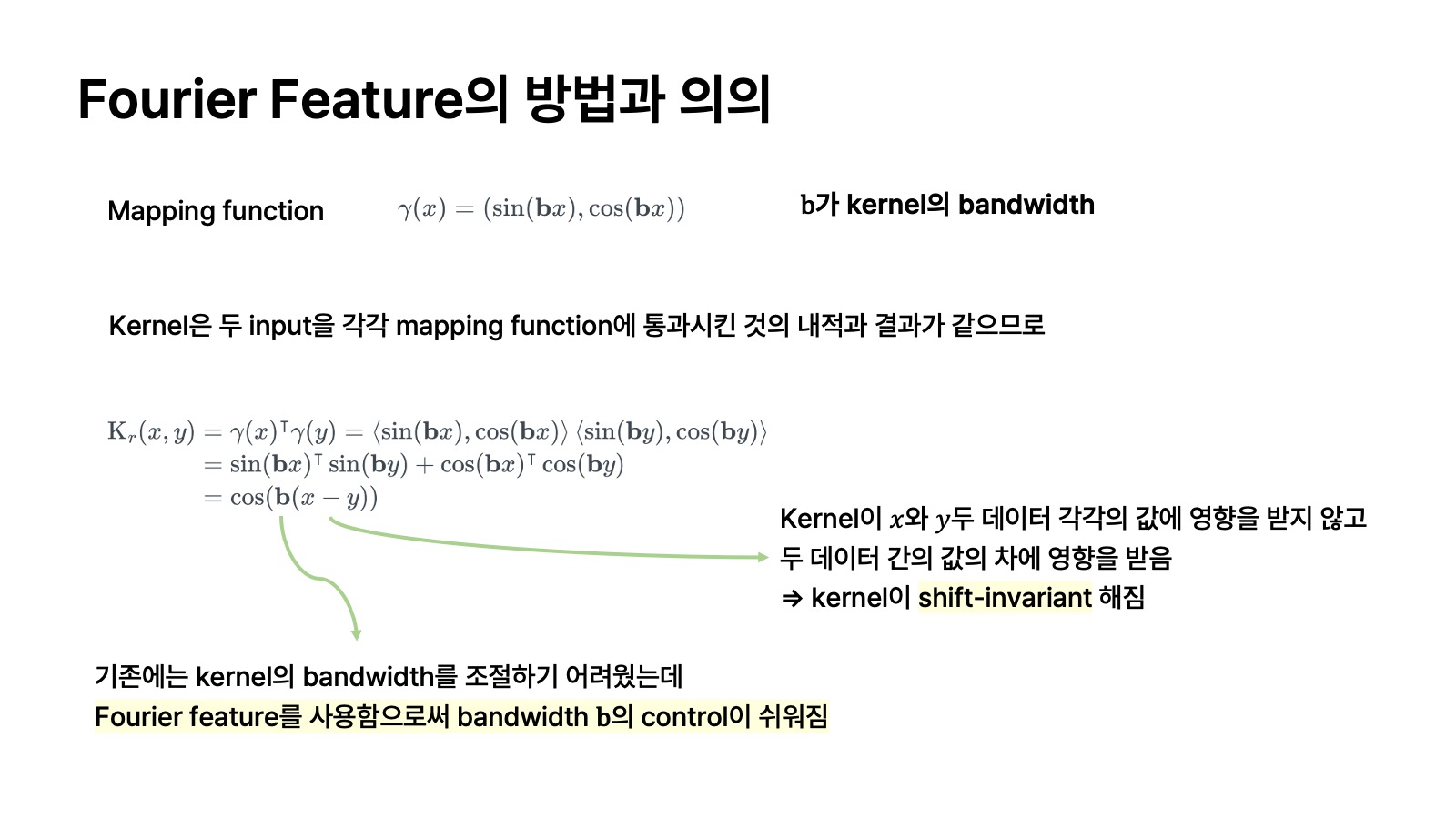
그러면 왜 fourier feature로 input을 mapping 했을 때 network의 NTK가 shift-invariant 해지고 bandwidth의 control이 쉬워지는지 그 이유는 다음과 같다.
먼저 Fourier feature를 사용한 mapping function을 다음과 같이 정의한다고 가정한다.
여기서 mapping function으로서 fourier basis 요소의 주파수(frequency)인
결국

논문에 표현된 식으로 좀 더 자세히 써 보면 위의 그림처럼 유도할 수 있다. 여기서 mapping function인
논문에서는 Fourier feature를 적용한 input을 받는 neural network는 파라미터를 학습하는 과정이 그 network의 NTK와 어떠한 stationary kernel을 합성해서 kernel regression을 수행하는 것과 동일하다고 설명하고 있다. 여기서 stationary kernel이 바로 mapping function에 해당된다.
Fourier Feature의 실험 결과

위의 GIF는 positional encoding를 적용했을 때 모델이 더 높은 주파수의 데이터에도 집중하여 잘 학습할 수 있음을 보여주는 실험 결과이다.
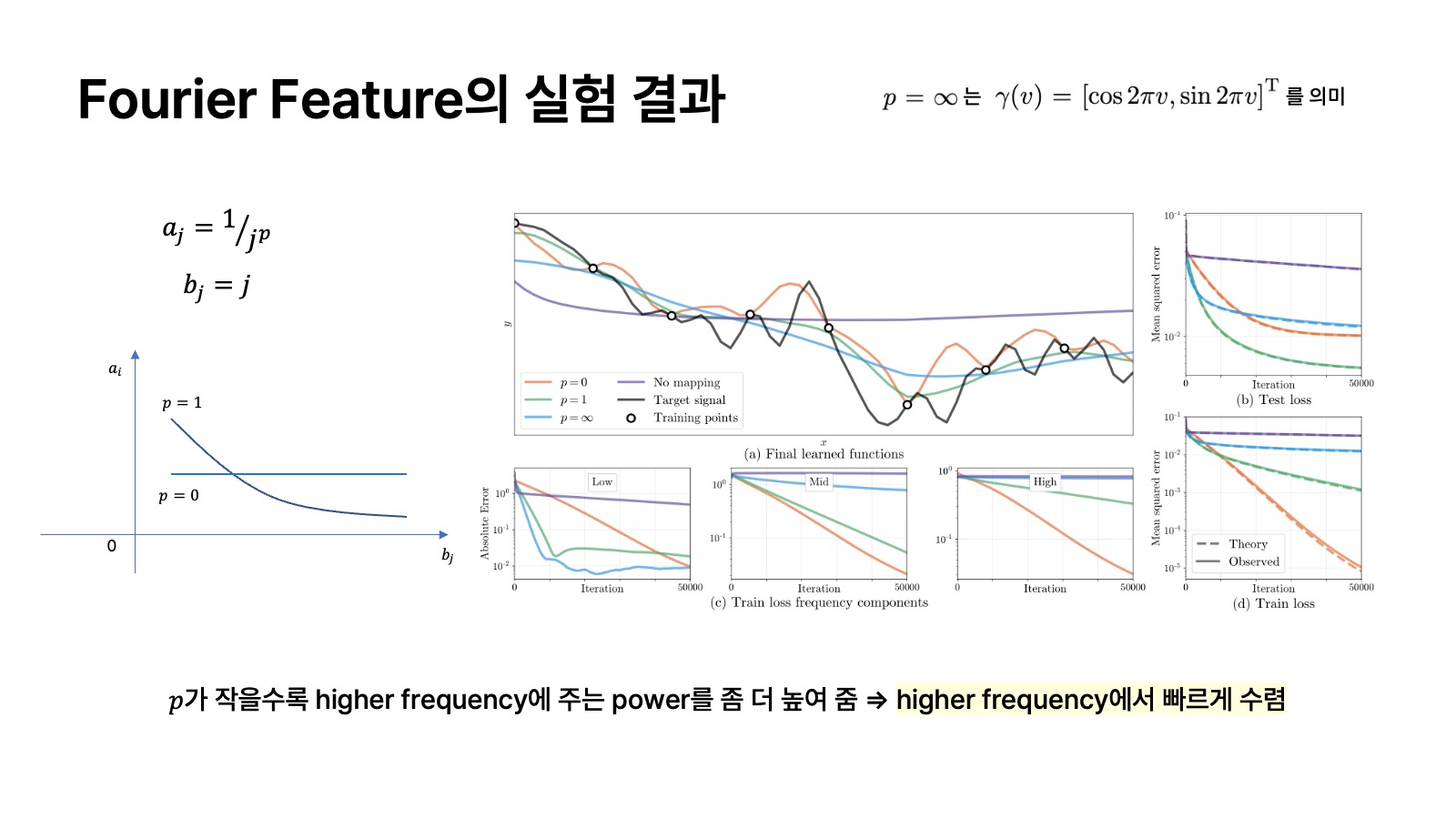
위의 실험 결과는 Fourier feature가 모델이 high frequency 데이터를 좀 더 잘 학습할 수 있다는 점을 보여준다. 여기서

위의 실험 결과는 kernel의 bandwidth인
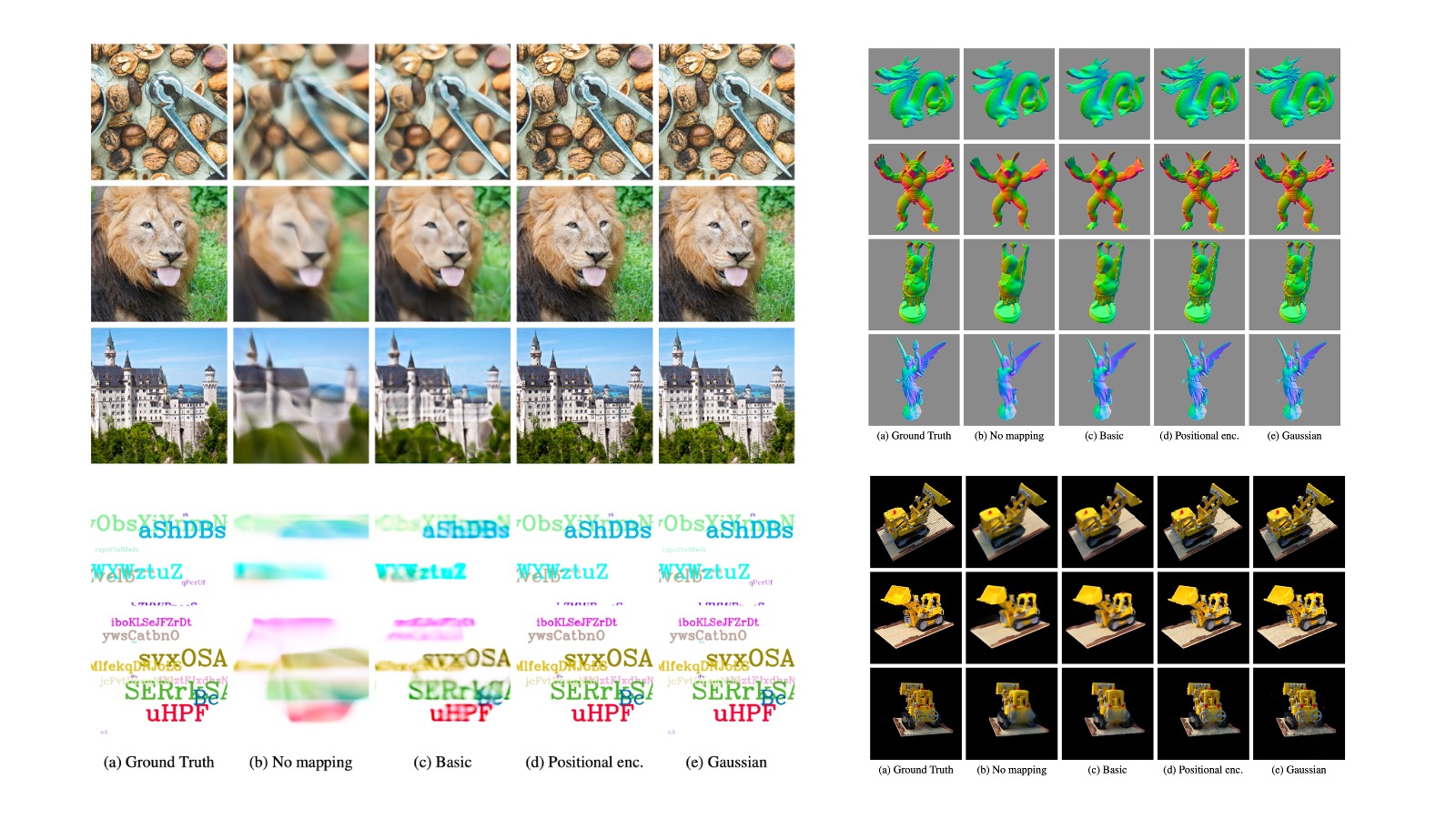
많은 실험 결과에서 Fourier feature로 positional encoding을 적용했을 때 모델이 high frequency의 데이터에 좀 더 집중하여 학습할 수 있음을 알려준다.
이 글 시리즈는 "Fourier Features Let Networks Learn High-Frequency Functions in Low Dimensional Domains" 논문을 바탕으로 한다.
Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains
We show that passing input points through a simple Fourier feature mapping enables a multilayer perceptron (MLP) to learn high-frequency functions in low-dimensional problem domains. These results shed light on recent advances in computer vision and graphi
arxiv.org
[이전 글]
Neural Tangent Kernel과 Fourier Features를 사용한 Positional Encoding (1) - Kernel Method
Positional encoding은 AI 모델링 분야에서 많이 쓰이는 기법 중 하나이다. 대표적으로 transformer에서도 데이터를 병렬 처리하여 학습하는 단점을 보완하여 데이터를 구성하는 각 token에 위치 정보를 부
glanceyes.com
Neural Tangent Kernel과 Fourier Features를 사용한 Positional Encoding (2) - Neural Tangent Kernel
이 글 시리즈는 'Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains' 논문과 이를 이해하는 데 필요한 선수 내용을 소개한 'Neural Tangent Kernel: Convergence and Generalization in Neural Networks'
glanceyes.com
출처
이 내용을 공부하고 글로 정리하는 데 있어서 큰 도움이 된 영상과 자료들이다.
1. https://youtu.be/9Jx2ulS1sAk, PR-374: Fourier Features Let Networks Learn High-Frequency Functions in Low Dimensional Domains
2. http://jnwoo.com/archive/6, Neural Tangent Kernel
3. https://rajatvd.github.io/NTK, Understanding the Neural Tangent Kernel
당신이 좋아할만한 콘텐츠
-
Generative Model과 Diffusion Model, 그리고 Denoising Diffusion Probabilistic Model 2023.06.23
-
DiffRF: Rendering-Guided 3D Radiance Field Diffusion 2023.05.05
-
PIFu: Pixel-aligned Implicit Function을 사용하여 single image로부터 clothed human 3D model을 예측하는 모델 2023.03.10
-
GRAF: Generative Radiance Fields for 3D-Aware Image Synthesis 2023.03.08
소중한 공감 감사합니다.