RNN의 기본 개념과 자연어 처리에서의 RNN 학습 과정

 

RNN(Recurrent Neural Network)

 

RNN에 관해 이전에 여러 번 포스팅을 했지만, 이전에 다루지 못한 개념을 좀 더 보강하는 차원에서 다시 한 번 RNN에 관해 정리해 보았다.

 

 

[RNN(Recurrent Neural Network)]

https://glanceyes.tistory.com/entry/AI-Math-RNN-Recurrent-Neural-Network

RNN (Recurrent Neural Network)

 

 

[순차 데이터와 RNN 계열의 모델]

https://glanceyes.tistory.com/entry/Deep-Learning-RNNRecurrent-Neural-Network

순차 데이터와 RNN(Recurrent Neural Network) 계열의 모델

 

 

[PyTorch RNN 모델 사용 예제 - AG NEWS]

https://glanceyes.tistory.com/entry/PyTorch로-RNN-모델-구현해보기-AG-NEWS-뉴스-기사-주제-분류

PyTorch RNN 모델 사용 예제 - AG NEWS 기사 주제 분류

 

 

[PyTorch RNN 모델 사용 예제 - CIFAR10]

https://glanceyes.tistory.com/entry/PyTorch-RNN-모델-사용-예제-CIFAR10-이미지-분류하기

PyTorch RNN 모델 사용 예제 - CIFAR10 이미지 분류하기

 

 

 

RNN(Recurrent Neural Network)란?

 

RNN(Recurrent Neural Network)은 입력 또는 출력 데이터가 sequence로 주어진 상황에서 각 time step에서 들어오는 입력 벡터 $x_t$와 그 전 time step의 RNN 모듈에서 계산한 hidden state인 $h_{t-1}$을 입력으로 받아서 현재 time step에서의 hidden state인 $h_t$를 출력하는 구조를 지니고 있다.

NLP에서는 각 time step에서 들어오는 입력 벡터가 주로 단어일 것이다.

 

중요한 점은 서로 다른 time step에서 들어오는 입력 데이터를 처리할 때 동일한 파라미터를 가진 모듈을 사용한다는 것이며, 같은 모듈을 재귀적으로 학습하므로 "Recurrent"라는 명칭을 지닌다.

 

 

 

$$ h_t = f_W(h_{t-1}, x_t) $$

 

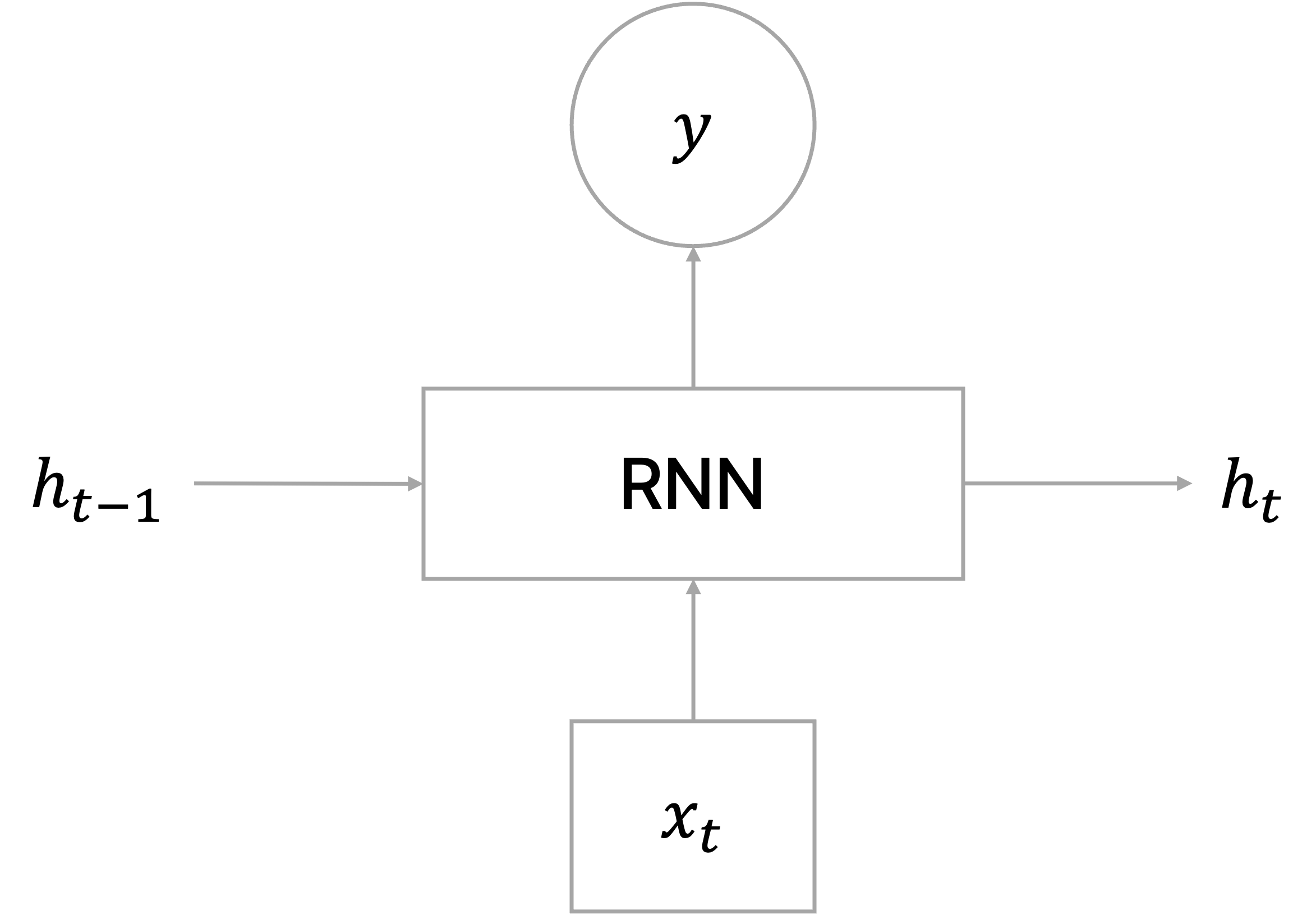
위의 식에서 쓰이는 변수를 정리하면 다음과 같다.

 

$h_{t}$: time step $t$에서 출력하는 hidden state

$h_{t-1}$: 이전 time step $t-1$에서 출력한 hidden state

$x_t$: time step $t$에서의 입력 벡터 $x_t$

$W$: RNN 모듈에 필요한 linear transformation matrix을 정의하는 파라미터

$f_W$: $W$를 파라미터로 지니는 RNN 함수

 

 

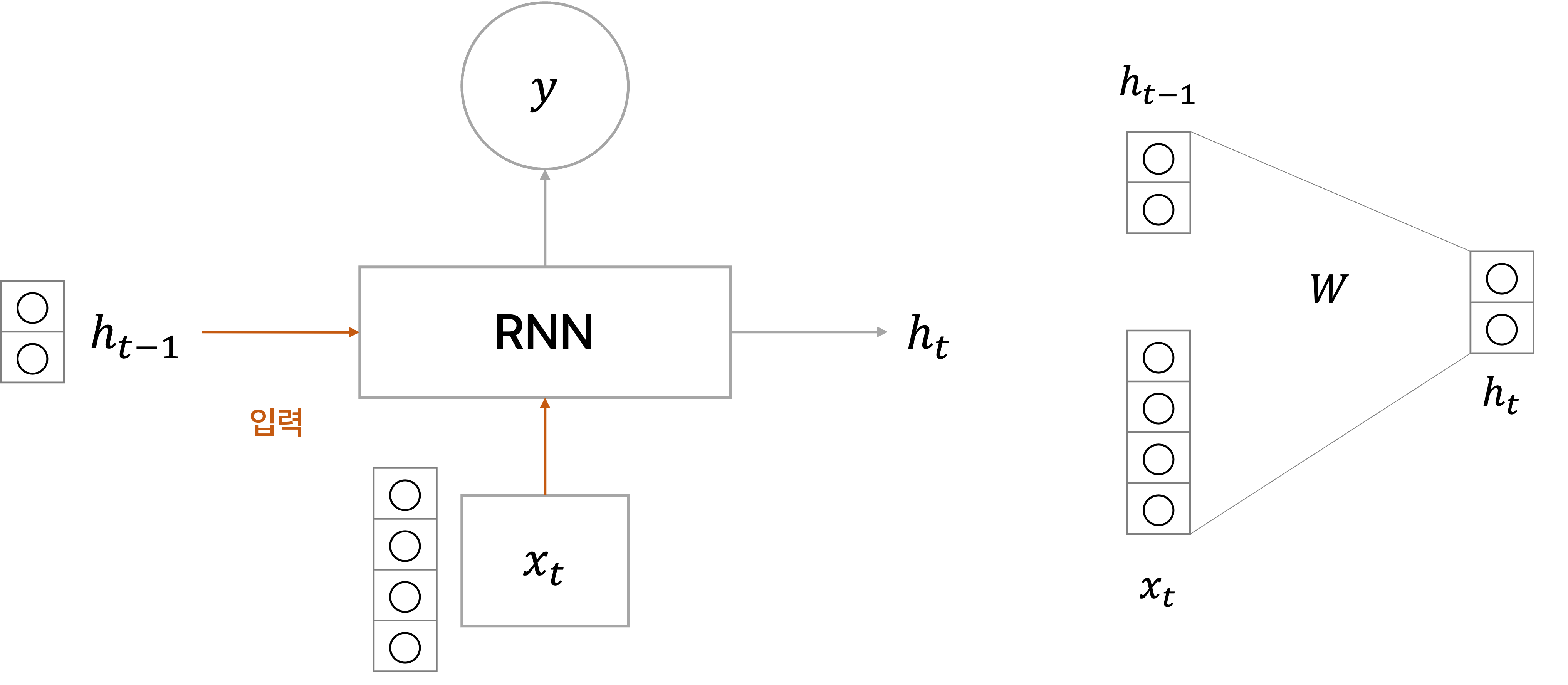
다시 한 번 정리하지만 RNN 모듈에서 사용하는 파라미터 $W$는 모든 time step에서 공유되면서 학습이 이루어진다는 점이 중요하다.

 

$$ \begin{align} h_t &= f_w(h_{t-1}, x_t)\\ h_t &= \tanh(W_{hh}h_{t-1} + W_{xh}x_t) \end{align} $$

 

예를 들어, 입력 벡터의 차원 크기가 4이고, hidden state의 차원의 크기가 2이라고 가정한다.

 

그러면 time step $t$에서는 $x_t$와 $h_{t-1}$을 입력으로 하여 파라미터 $W$와의 연산을 통해 출력 $h_t$를 내보내야 한하는데, 이를 fully connected layer의 선형변환 행렬인 파라미터 $W$를 사용하는 모델로 나타내면 다음과 같다.

 

 

 

이를 행렬 곱으로 표현하면 다음과 같으며, 이때의 파라미터 행렬 $W$의 차원은 $2 \times 6$가 될 것이다.

 

 

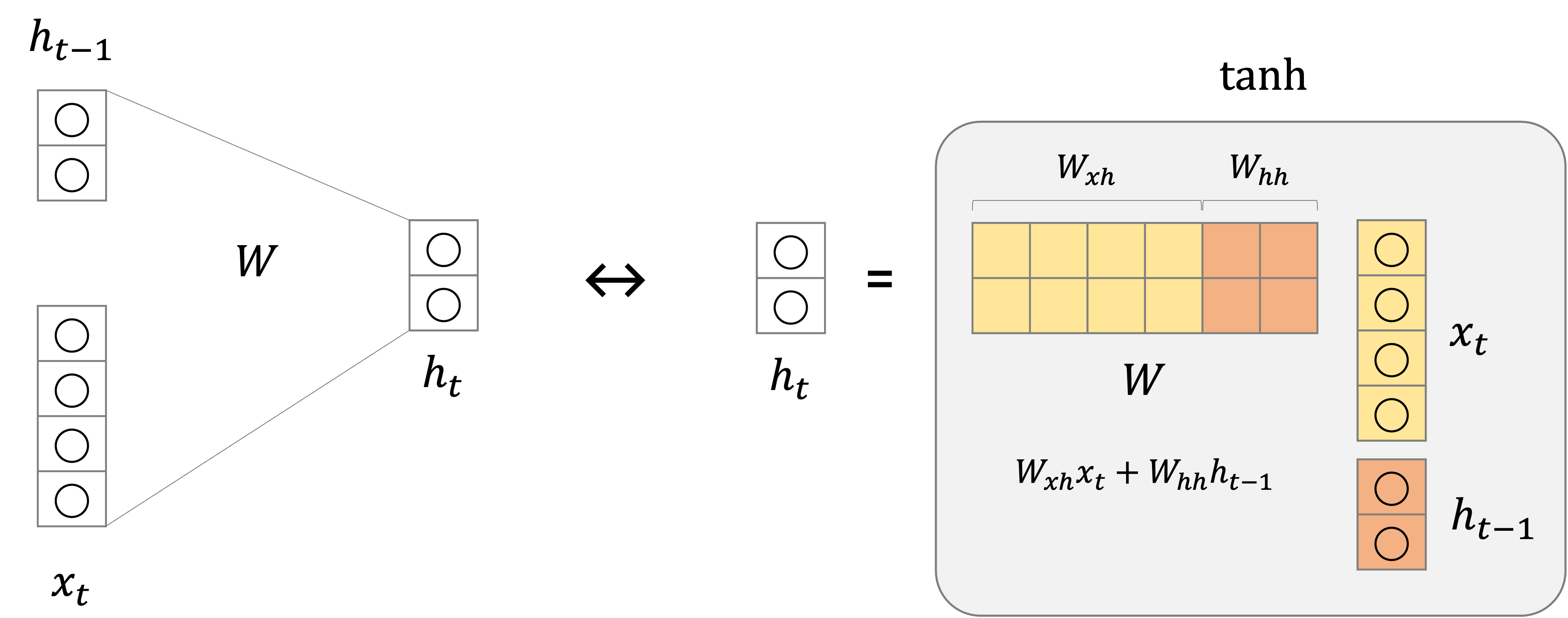
여기서 $W_{xh}$와 $W_{hh}$는 $W$를 구성하는 부분행렬이며, $W_{xh}$는 $x_t$를 가지고 $h_t$의 일부로 변환하고, $W_{hh}$는 $h_{t-1}$을 가지고 $h_t$의 일부로 변환하는 행렬이다.

 

첫 time step에서는 이전 time step이 존재하지 않아서 입력으로 오는 $h_0$를 hidden state의 차원 크기를 지니고 값이 0으로 채워진 벡터 또는 행렬로 설정한다.

주목해야 할 점은 hidden state인 $h_t$는 이전 time step 뿐만이 아니라 그 전 time step에도 있던 정보를 모두 다 지니고 있는 상태라는 것이다.

 

 

또한 매 time step에서 출력할 hidden state를 계산한 후 어떤 특정 time step에서는 RNN을 사용하는 태스크에 맞는 출력값 $y$를 계산해야 하며, 해당 time step의 hidden state를 가지고 $y$를 계산한다.

 

$$ y_t = W_{hy}h_t $$

 

$h_t$를 입력으로 받는 output layer에서 선형 변환을 해주는 파라미터 $W_{hy}$를 곱함으로써 최종적으로 어떠한 태스크의 예측값으로 해석 가능한 $y_t$를 구할 수 있다.

임의의 time step $t$에 관한 $y_t$는 매 time step 마다 계산해야 할 수도 있고, 아니면 마지막 time step에만 계산해야 할 수도 있다.

예를 들어, 문장에서 각 단어의 중요도나 품사를 예측할 때는 출력인 $y_t$를 매 time step 마다 계산할 필요가 있고, 문장 전체의 감정을 분석하는 태스크에서는 마지막 time step에서만 출력 $y_t$를 계산해도 된다.

 

 

$y_t$의 차원은 RNN을 어떠한 태스크의 용도로 사용하느냐에 따라 달라질 것이다.

예를 들어, 이진 분류(Binary Classification)에서 $y_t$는 1차원이며, 주로 sigmoid 같은 활성 함수를 적용하여 0에서 1 사이의 확률 값을 지닌다고 해석할 수 있다.

다중 레이블 분류(Multi-label Classifcation)에서 $y_t$는 전체 레이블의 수만큼의 차원을 지닌 벡터이며, 주로 softmax 레이어를 통과하여 어떠한 분류에 속할 확률이 높은지에 관한 확률 분포를 얻을 수 있다.

 

 

 

RNN의 구조에 따른 종류

 

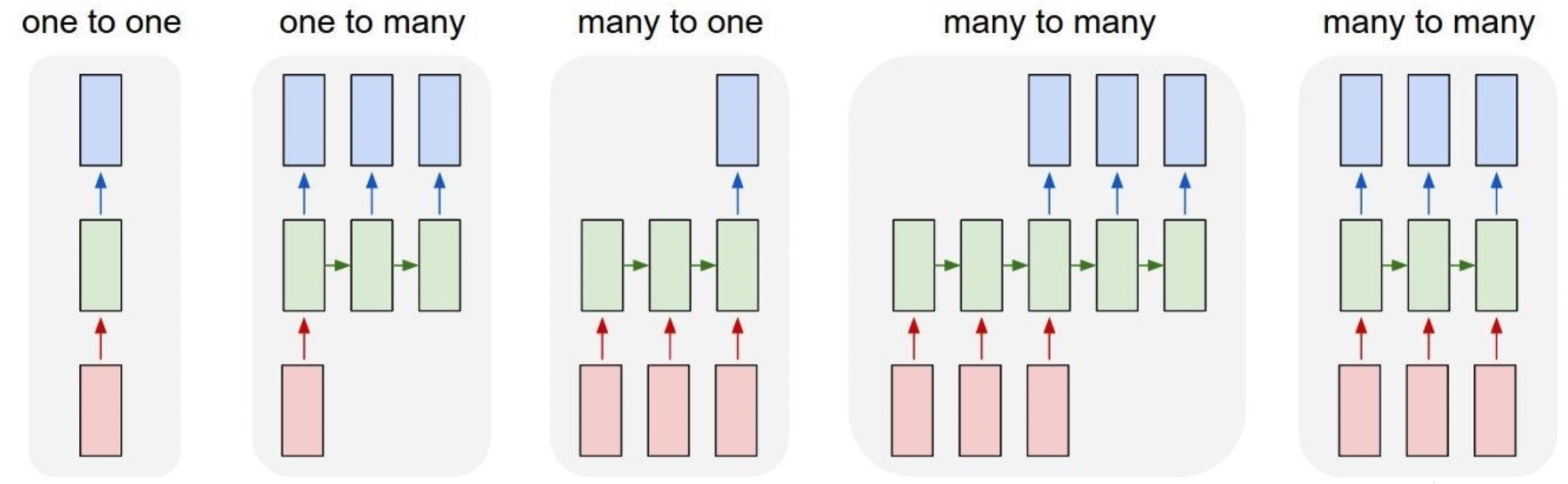
[출처] http://karpathy.github.io/2015/05/21/rnn-effectiveness, Andrej Karpathy

 

 

One to One

입력과 출력의 time step가 단 하나인 구조이며, 일반적인 신경망 구조를 도식화한 것으로 이해할 수 있다.

 

 

One to Many

입력이 하나의 time step로 이루어지고, 출력은 여러 time step으로 이루어지는 구조이며, 대표적으로 이미지를 설명할 수 있는 문장을 만드는 image captioning이 해당된다.

예를 들어, 입력으로 어떤 단일 이미지가 주어지고, 이미지의 설명을 생성하기 위해 그에 필요한 단어를 각 time step별로 생성하는 것으로 볼 수 있다.

그러나 앞서 설명한 것에 따르면 RNN 모듈에서는 입력이 반드시 들어가야 하는데, One to Many 구조에서는 다른 time step에서 첫 번째 time step에서 들어가는 입력과 같은 크기의 벡터 또는 행렬이 주어지되 그 값이 모두 0으로 채워진 것을 사용한다.

 

 

Many to One

입력을 sequence로 받지만 최종 출력을 마지막 time step에서 구하는 구조이며, 대표적으로 주어진 문장에 대한 감정 분석을 처리할 때 사용할 수 있다.

예를 들어, "Everybody loves you."라는 문장이 주어지면 각 단어의 임베딩 벡터가 매 time step 마다 입력으로 들어가고, 마지막 time step의 hidden state를 가지고 최종적인 output을 구해 입력 문장이 감정적으로 긍정임을 예측한다.

 

 

Many to Many

입력과 출력이 모두 sequence 형태를 갖는 구조이며, 대표적으로 machine translation 태스크에서 주로 사용한다.

입력을 받고 바로 출력을 구하는 구조로 만들 수도 있고, 아니면 입력을 받는 RNN 모듈 구간과 출력을 구하는 RNN 모듈 구간이 일치하지 않는 구조로 만들 수도 있다.

입력을 바로 받고 출력을 구하는 구조를 사용하는 태스크에는 각 단어의 품사를 구하는 PoS(Part of Speech), 비디오의 각 프레임이 어떠한 scene인지 실시간으로 구하는 video classification이 있다.

 

 

 

RNN과 Character-level Language Model

 

Language Model이란?

 

주어진 문자열 또는 단어의 순서를 바탕으로 그 다음으로 올 단어가 어떤 것인지를 예측하는 태스크의 모델이다.

Language 모델은 word-level과 character-level 모두 수행할 수 있다.

 

 

Character-level Language Model 예시

 

'artificial'이라는 문자열 sequence이 학습 데이터로 주어졌을 때, 가장 먼저 해야할 일은 character-level에서 사전을 구축해야 하는 것이다.

주어진 학습 데이터 sequence에서 등장하는 character를 중복없이 모아서 사전을 구축한 후, word embedding 과정에서와 같이 각각의 character는 사전의 크기 만큼의 차원을 지니는 one-hot vector로 나타낸다.

 

 

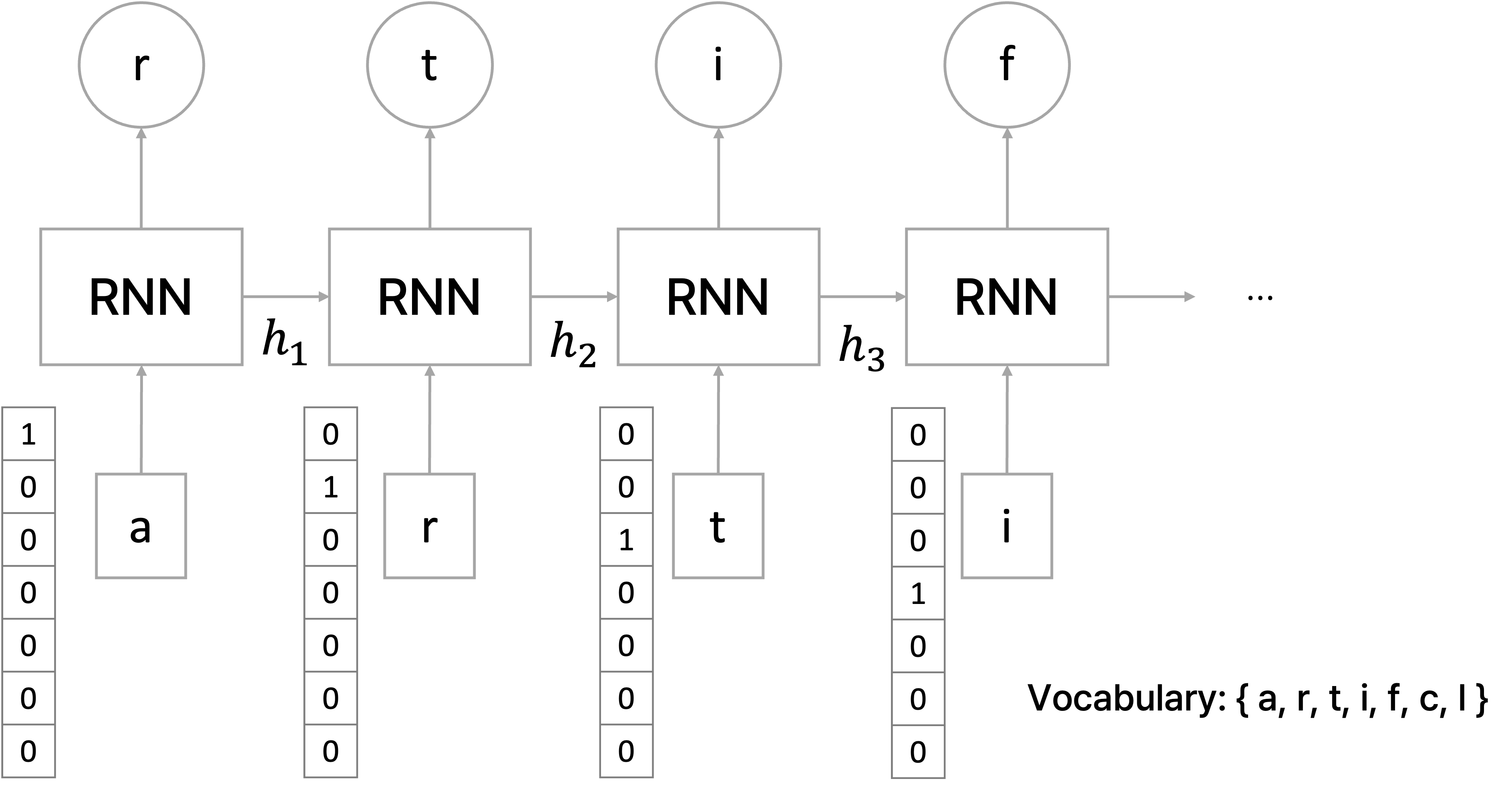
그러면 'arfiticial'에서 'a' 다음으로 올 것으로 예측해야 하는 문자는 'r', 'r' 다음으로 올 것으로 예측해야 하는 문자는 'f' 등 각 문자별로 다음 위치에 오게 될 문자를 예측해야 한다.

 

RNN을 가지고 각 time step $t$에서의 hidden state를 구하는 과정은 다음과 같이 정리할 수 있다.

 

$$ h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b) $$

 

위에서 정리했던 RNN의 hidden state 구하는 식과 유사하며, 여기서는 추가적으로 bias term까지 함께 고려했다.

 

각 time step에서 계산되는 output도 마찬가지로 bias term을 고려하여 정의할 수 있다.

 

$$ y_t = W_{hy}h_t + b $$

 

이 태스크에서는 기존에 구축한 사전에서 다음으로 어떤 문자가 올지를 예측해야 하므로 사전의 크기와 같은 차원을 지니면서 사전의 각 문자가 등장할 확률을 나타내는 벡터로 나타내야 한다.

따라서 $y_t$는 $\text{logit}$처럼 어떠한 문자가 등장할 확률이 높은지를 나타내게 되고, 등장 확률이 가장 높은 문자를 구하기 위해 softmax 함수를 통과한다.

 

 

Test 단계에서 inference를 할 때는 오로지 첫 번째 입력에만 문자를 주고 해당 time step에서 다음 문자를 예측하여 이를 다음 time step의 입력으로 주어지도록 하여 마지막에 올 문자까지 차례로 예측한다.

 

 

 

RNN의 학습 과정과 문제점

 

BPTT(Backpropagation Through Time)

 

BPTT란?

 

전반적인 Many to Many 구조의 RNN을 학습하는 과정을 정리하면 다음과 같다.

 

1. 매 time step마다 입력이 주어진다.
2. 이전 time step에서 오는 hidden state와 현재 time step에서 온 입력을 가지고 현재 time step에서 출력할 hidden state를 구한다.
3. 구한 hidden state를 가지고 현재 time step의 output을 계산한다.
4. 예측한 output과 ground truth 간의 loss를 구하고, 모든 time step에 관해 이 loss를 줄이는 방향으로 학습한다.

 

그런데 RNN은 일반적인 fully connected layer 모델과는 달리 각 파라미터들이 네트워크의 매 time step마다 공유된다.

즉, 각 time step의 출력에서의 gradient는 현재 시간 스텝에서의 계산에만 의존하는 것이 아니라 이전 시간 스텝에도 의존한다.

그래서 원래의 backpropagation과 비슷하지만, 차이점은 매 time step마다 파라미터 $W$에 관한 gradient를 더해주는 것이다.

 

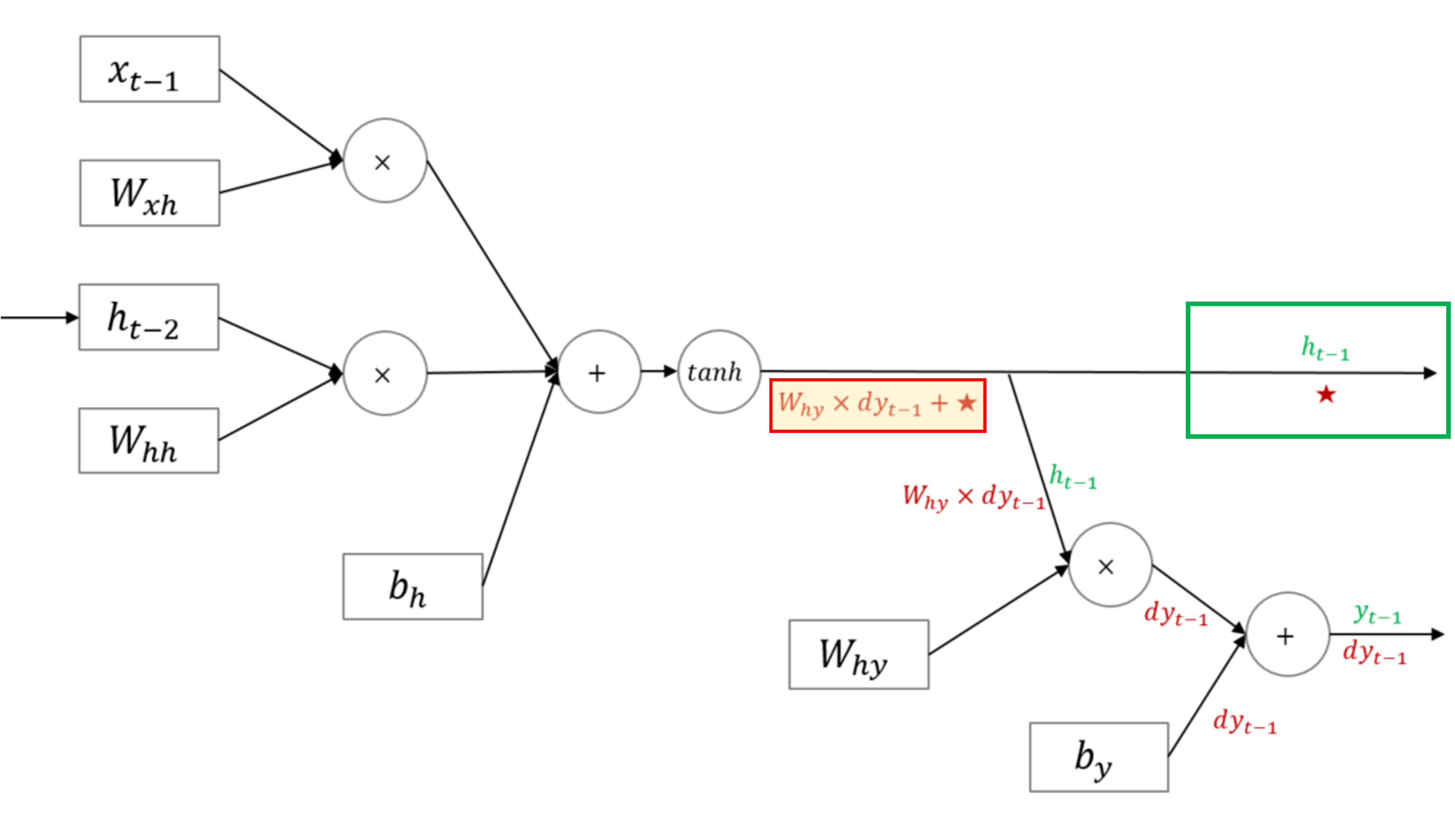
[출처] https://ratsgo.github.io/natural%20language%20processing/2017/03/09/rnnlstm

RNN에서는 hidden state가 계속 recurrent하게 입력으로 들어오는 구조이므로 $dh_{t-1}$ 은 $t-1$ 시점의 출력값에 관한 loss에 의해 구해진 gradient인 $W_{hy} dy_{t-1}$ 뿐 아니라 위의 이미지에서 출력으로 나가는 hidden state인 ★에 해당하는 gradient 또한 더해져 동시에 반영된다.

 

 

 

 

Truncated Backpropagation Through Time

 

 

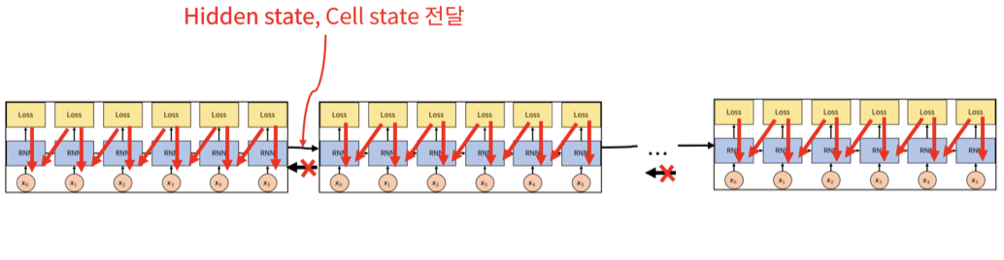
그런데 현실적으로 학습 데이터로 매우 긴 길이의 sequence가 입력으로 주어질 때, 각 time step의 output을 계산하여 GT와의 차이를 줄이는 방향으로 학습하기에는 한정된 GPU와 메모리 자원으로 한꺼번에 처리하는 데 무리가 있다.

그래서 이를 truncation하여 제한된 길이의 sequence만으로 학습을 진행하는 방식을 택할 수 있다.

즉, 한번에 학습할 수 있는 sequence의 길이를 제한하여 RNN의 파라미터를 학습하는 것이다.

 

시간 축 방향으로 너무 길어진 신경망을 적당한 지점에서 잘라내어 작은 신경망 여러 개로 만들어 잘라낸 작은 신경망에서 역전파를 수행한다고 볼 수 있다.

길이 $T$로 쪼개진 truncation 사이에서는 기울기 역전파가 이루어지지 않으며, 이는 time step이 $T$ 이상 떨어진 입-출력 관계는 학습되지 않는다는 것이다

 

 

 

RNN에서의 Vanishing or Exploding Gradient Problem

 

 

 

Time step에서의 hidden state 관점에서 매 time step마다 동일한 파라미터를 마치 등비수열처럼 곱하게 되므로, 과거의 time step에서의 정보가 hidden state에 잘 반영되지 않거나 너무 크게 반영되는 현상이 있다.

그래서 backpropagation을 통해 과거의 gradient를 구할 때 이 gradient의 크기가 소멸될 정도로 매우 작아지거나 폭발적으로 커지는 문제가 발생할 수 있다.

 

예를 들어, RNN의 각 파라미터를 loss를 줄이는 방향으로 업데이트 할 때 첫 time step에서의 hidden state $h_1$의 gradient를 계산해야 하는데, output $y$를 구하는 과정에서 hidden state $h_1$이 계속 RNN 모듈을 통과하며 파라미터 $W_{hh}$가 곱해지고 매번 활성함수를 적용하는 단계를 반복한다.

그러면 $\frac{\partial{y}}{\partial{h_1}}$를 구하는 과정에서 sequence의 길이가 길어질수록 활성함수를 미분한 값과 파라미터 $W_{hh}$를 sequence의 길이만큼 곱하면서 이 편미분 값이 매우 작아지거나 커질 가능성이 있을 수 있다.

 

 

출처
1. 네이버 커넥트재단 부스트캠프 AI Tech NLP Track 주재걸 교수님 기초 강의