Bayes 정리와 사후 확률, 증거에 관한 자세한 내용은 아래의 글을 참고하시기 바랍니다.
https://glanceyes.tistory.com/entry/인공지능-기초-Uncertainty-1-확률적인-추정을-위한-확률과-사건-그리고-명제
[인공지능 기초] Uncertainty (1) - 확률적인 추정을 위한 확률과 사건, 그리고 명제
들어가기 전에 이 세상의 많은 일들은 확률적인 경우가 많다. 그 상황에서 우리는 자신의 목적에 가장 부합하면서 확률적으로 발생 가능성이 높거나 낮은 것을 고려하여 최선의 선택을 하려고
glanceyes.com
https://glanceyes.tistory.com/entry/인공지능-기초-Uncertainty2-결합-확률과-조건부-확률-그리고-베이즈-정리
[인공지능 기초] Uncertainty(2) - 결합 확률과 조건부 확률 그리고 베이즈 정리
들어가기 전에 지난 글에서 우리는 이 세상의 많은 일들이 확률에 의존한다는 것을 알았고, 사건에 관한 확률을 다룰 때 명제로 표현하여 사용한다는 점을 확인했다. 또한 증거(evidence)가 기존에
glanceyes.com

나이브 베이즈 정리

베이즈 정리란?
- 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리
이 용어의 정의를 알아보기 전에 조건부 확률부터 알아볼 필요가 있다.

조건부 확률

$$P(A | B) = \frac{P(A \cap B)}{P(B)}$$
- 전제: 두 사건 A, B가 있고, 사건 B가 발생한 이후에 사건 A가 발생한다고 가정한다.
- 정의: 사건 B가 일어난 후 사건 A가 일어날 확률이다.
- $P(A)$: 사건 A가 일어날 확률
- $P(B)$: 사건 B가 일어날 확률 = 사건 A가 발생하기 전 사건 B가 일어날 확률 = 사전확률
- $P(A|B)$: 사건 B가 일어난 후 사건 A가 일어날 확률 = 조건부 확률
- $P(B|A)$: 사건 A가 일어났을 때 사건 B가 앞서 일어났을 확률 = 사후확률 (사후확률도 조건부 확률에 속함)

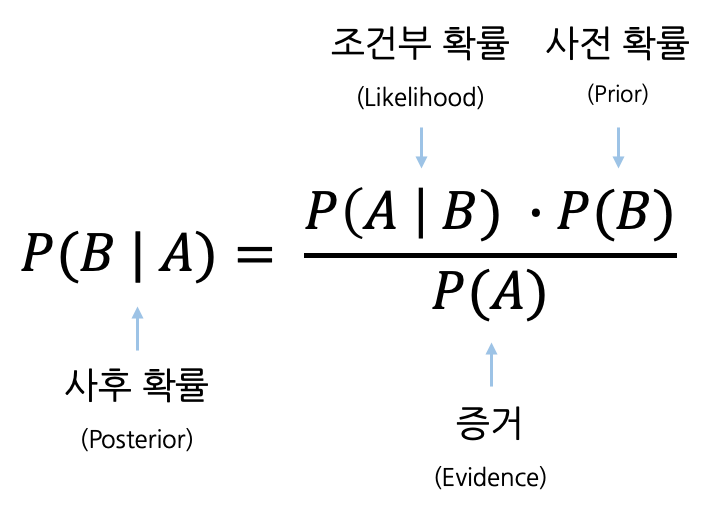
$$P(A | B)= \frac{P(B | A) \cdot P(A)}{P(B)}$$
여기서 사후확률과 가능도(likelihood) 모두 조건부확률이다. 우변에서의 조건부 확률은 likelihood라고 보는 게 더 정확할 것이다.
베이즈 정리의 의미는 무엇이고, 왜 통계에서 중요할까? 다음 예시를 들어보자.

베이즈 정리의 의미
- 감염증 A에 걸린 사람의 40%가 마스크를 미착용한 사람들이다. 그러면 60%가 마스크를 착용했음에도 감염증 A에 걸렸다는 것인데, 이는 과연 마스크를 착용하는 것이 더 위험하다는 걸 의미할까?
- 전체 마스크를 착용한 사람과 착용하지 않은 사람의 비율을 알아야 한다.

수학적으로 다음과 같이 정의해보자.
- $P(A)$: 감염증 A에 걸릴 확률
- $P(~A)$: 감염증 A에 걸리지 않을 확률
- $P(M)$: 마스크 착용자 비율
- $P(~M)$: 마스크 미착용자 비율

문제에서 알 수 있는 정보는 다음과 같다.
- $P(~M|A) = 0.4$ ⇒ 감염증 A에 걸린 사람 중 마스크를 착용하지 않았던 사람의 비율
- $P(M|A) = 0.6$ ⇒ 감염증 A에 걸린 사람 중 마스크를 착용했던 사람의 비율
문제에서 알고 싶어하는 정보는 다음과 같다.
- $P(A|M)$ ⇒ 마스크를 착용한 사람 중 감염증 A에 걸린 사람의 비율
- $P(A|~M)$ ⇒ 마스크를 착용하지 않은 사람 중 감염증 A에 걸린 사람의 비율

$$P(A | M)= \frac{P(M | A) \cdot P(A)}{P(M)} = \frac{0.6 \cdot 0.01}{0.9} ≈ 0.0067$$
$$P(A | ~M)= \frac{P(~M | A) \cdot P(A)}{P(~M)} = \frac{0.4 \cdot 0.01}{ 0.1} ≈ 0.04$$
마스크를 쓸 때보다 마스크를 쓰지 않을 때 감염증 A에 걸릴 확률이 약 6배 높다.

나이브 베이즈 분류

나이브 베이즈 분류(Naive Bayesian Classification)란?
- 데이터의 특징을 가지고 각 클래스(레이블)에 속할 확률을 계산하는 조건부 확률 기반의 분류 방법
- 데이터의 특징이 모두 상호 독립적이라는 가정하에 확률 계산을 단순화한다 ⇒ 나이브(naïve)하다
- Bayes Theorem에 의해 데이터의 특징을 통해 클래스 전체의 확률 분포 대비 특정 클래스에 속할 확률을 구하는 것이다.
나이브 베이즈 분류를 통해 데이터 특징이 하나 이상일 때 나이브 베이즈 공식으로 해당 데이터가 어떤 레이블에 속할 확률이 가장 높은지를 알 수 있다.

결합 확률
$$P(X, Y) = P(X | Y) \cdot P(Y)$$
- 나이브 베이즈 알고리즘에서는 X, Y 사건이 독립이라고 가정하므로 다음과 같은 식이 성립할 수 있다.
$$P(X, Y) = P(X | Y) \cdot P(Y) = \frac{P(X \cap Y)}{ P(Y)} \cdot P(Y) = P(X \cap Y) = P(X) \cdot P(Y)$$

결합확률과 베이즈 정리
데이터의 특징을 X, Y라고 하고, 전체 레이블 중 하나를 A라고 하자.
$$P(A | X, Y) = \frac{P(X, Y | A) \cdot P(A)}{P(X, Y)} \qquad \text{by Bayes Theorem}$$
- $P(A)$ ⇒ 데이터가 레이블 A에 속할 확률
- $P(X, Y | A)$ ⇒ 레이블이 A인 데이터가 X, Y 특징을 모두 가질 확률
- $P(X, Y)$ ⇒ 데이터가 X, Y 특징을 모두 가질 확률
- $P(A | X, Y)$ ⇒ X, Y 특징을 모두 갖는 데이터가 레이블 A에 속할 확률

$$P(X, Y) = P(X) \cdot P(Y) $$
베이즈 정리에서는 어떤 한 데이터가 각 특징을 갖는 사건끼리 서로 독립이라고 가정한다.
$$P(X, Y | A) = P(X | A) \cdot P(Y | A)$$
따라서 레이블이 A인 데이터가 특징 X를 가질 사건과 특징 Y를 가질 사건은 서로 독립이다.
이를 종합하면 식을 다음과 같이 정리할 수 있다.
$$P(A | X, Y) = \frac{P(X | A) \cdot P(Y | A) \cdot P(A)}{P(X) \cdot P(Y)}$$
단, 데이터가 각 특징을 갖는 사건끼리 독립인 것이지, 특징과 레이블이 서로 독립이라는 의미가 아니다.
나이브 베이즈 분류 적용 예시로 받은 메일이 스팸 메일인지 아닌지를 판단하는 분류기를 들 수 있다.
어떤 한 메일의 내용을 키워드로 추출했을 때, 그 결과가 '광고', 'SNS', '결제'라고 하자. 이 키워드를 가지고 해당 메일이 스팸 메일인지 아닌지를 판단하는 분류기를 만들 때 나이브 베이즈 분류를 사용할 수 있다.

$$P(SPAM | AD, SNS, PAY) = \frac{P(AD | SPAM) \cdot P(SNS | SPAM) \cdot P(PAY | SPAM) \cdot P(SPAM)}{P(AD) \cdot P(SNS) \cdot P(PAY)}$$
'광고(AD)', 'SNS(SNS)', '결제(PAY)' 키워드를 갖는 메일이 스팸(SPAM)일 확률을 구한다.
단, 메일이 '광고', 'SNS', '결제'라는 각 키워드를 가질 사건은 서로 독립이라고 가정한다.
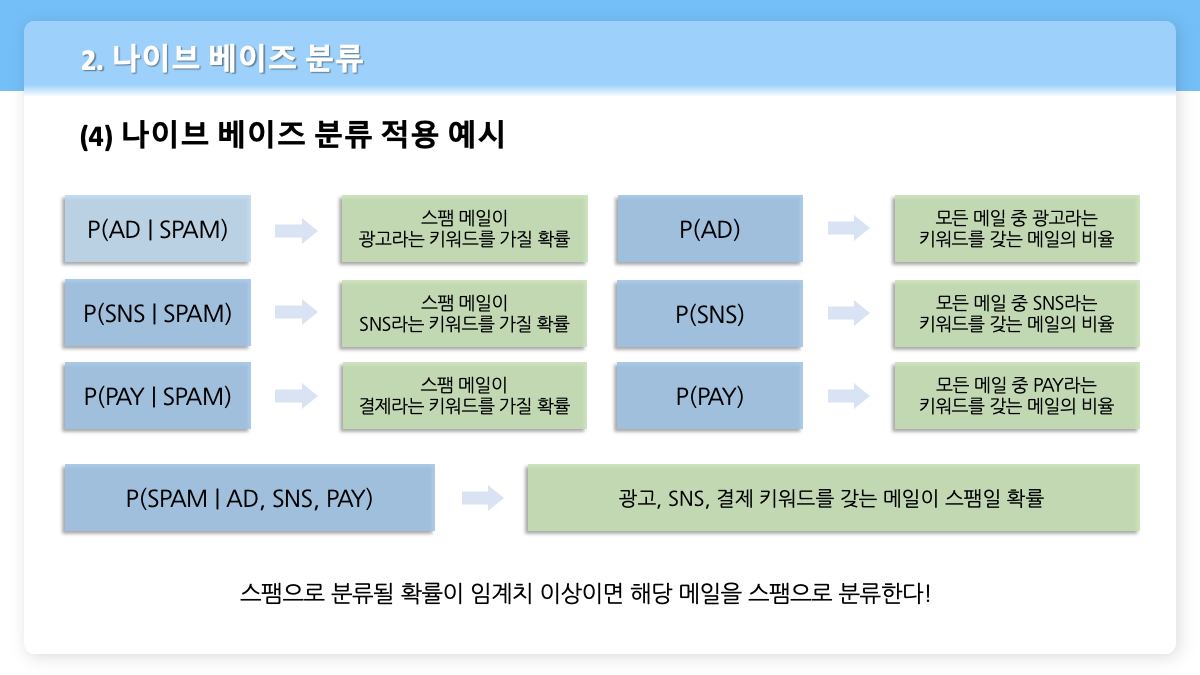
- $P(AD | SPAM)$ ⇒ 스팸 메일이 '광고'라는 키워드를 가질 확률
- $P(AD)$ ⇒ 모든 메일 중 '광고'라는 키워드를 갖는 메일의 비율
- $P(SNS | SPAM)$ ⇒ 스팸 메일이 'SNS'라는 키워드를 가질 확률
- $P(SNS)$ ⇒ 모든 메일 중 'SNS'라는 키워드를 갖는 메일의 비율
- $P(PAY | SPAM)$ ⇒ 스팸 메일이 '결제'라는 키워드를 가질 확률
- $P(PAY)$ ⇒ 모든 메일 중 'PAY'라는 키워드를 갖는 메일의 비율
- $P(SPAM | AD, SNS, PAY)$ ⇒ '광고', 'SNS', '결제' 키워드를 갖는 메일이 스팸일 확률