[인공지능 기초] Uncertainty (1) - 확률적인 추정을 위한 확률과 사건, 그리고 명제
- -
들어가기 전에
이 세상의 많은 일들은 확률적인 경우가 많다. 그 상황에서 우리는 자신의 목적에 가장 부합하면서 확률적으로 발생 가능성이 높거나 낮은 것을 고려하여 최선의 선택을 하려고 한다. 그러면 그 확률이란 것에 주목해야 할 필요가 있지 않을까? 이번 시리즈 글에서는 확률에 관한 정의와 이와 관련한 대표적인 정리들을 소개하고자 한다. 그전에 확률과 관련한 정의를 알아보고, 확률과 명제가 어떠한 관계가 있는지 알아보자.
불확실성과 결정
우리는 일상 생활에서 여러 문제점들을 맞닥뜨리고 이를 해결하고자 노력한다. 꼭 중요한 시험 문제를 풀어서 맞추는 것 뿐만이 아니라 출근해야 하는데 늦게 기상을 해서 어떠한 교통 수단을 이용해야 할지, 어떤 점심 메뉴를 선택해야 좀 더 맛있는 음식을 저렴하게 먹을 수 있는지 등 사소하면서도 다양한 문제를 마주하게 된다. 그러한 문제들 중 일부는 어떠한 행동이나 해결책을 취했을 때 반드시 그에 대응되는 결과가 나올 때도 있지만, 대체로 확률적으로 결과가 나올 때가 많을 것이다.

간단한 예를 들어보자. 우리가 출국 비행기를 타려면 공항에 가야 하는데, 이 이륙편을 놓치지 않기 위해서는 최소한 몇 분 전에 공항으로 출발하는 것이 바람직할까? $t$분 전에 공항으로 출발한다고 하더라도 그 결정이 반드시 비행기에 제 시간에 탑승할 수 있다고 보장해 줄 수 있을까? 공항 가는 길에 도로 공사로 인해 교통 체증이 발생해서 공항에 가는 소요 시간이 예상보다 길게 걸릴 수도 있고, 자동차의 연료가 부족하여 가는 도중에 주유소를 들려서 기름을 넣을 수도 있다. 그러면 우리가 가능한 일찍 공항으로 출발하면 출발할수록 이륙편에 제 시간에 탑승할 확률은 높아지므로 가능한 빨리 출발하는 게 이득일 수 있겠다.
하지만 그렇다고 이륙 하루 전에 공항에 가서 밤을 새워 기다리는 게 과연 바람직한 선택일까? 공항에서 하룻밤 노숙하는 걸 원하는 사람이라면 만족스러운 방법일 수 있겠지만, 그렇지 않을 수도 있다. 그래서 우리는 어떤 문제에 관해 어떠한 행동(action)을 취할지를 결정(decision)할 때 확률적인 요소도 고려할 뿐만이 아니라 자신에게 큰 효용도 가져다 줄 수 있는 최선의 선택을 하고자 노력할 것이다. 여기서 효용이란 행동에 관한 선호도(preference)를 나타낸다고 보면 된다. 이륙편 출발까지 두 시간이 남았고, 공항에 도착하는 데 30분이 소요될 때 최소한 공항으로 세 시간 전에는 출발하는 방법이 이륙편을 놓칠 가능성도 낮은 편이고 너무 공항에서 오래 대기할 필요가 없으므로 가장 바림작하다고 생각하는 것처럼 말이다.
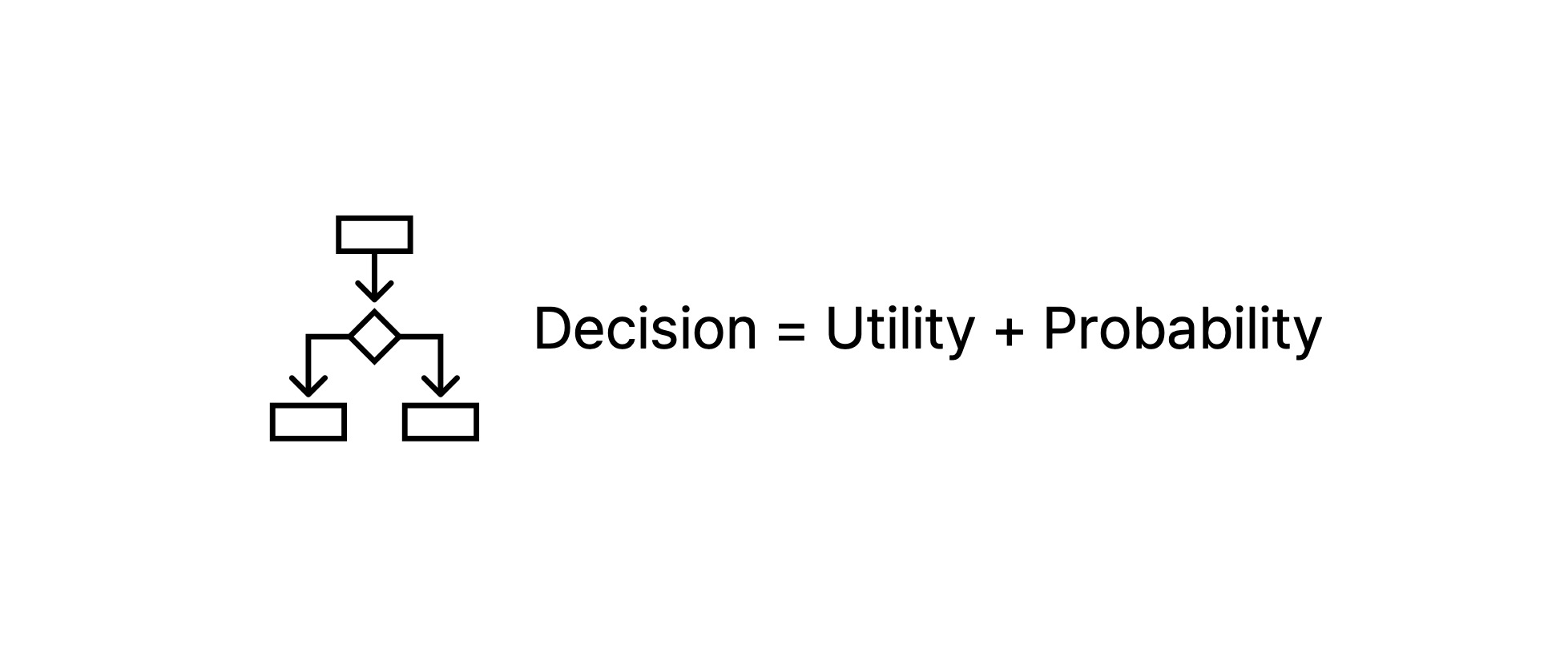
AI 에이전트(agent)도 여러 불확실성이 존재하는 문제를 해결하고자 확률을 고려한다. 에이전트는 자신에게 주어진 목적을 달성할 수 있는 확률이 높은 행동을 선택을 하기 위해 노력할 것이다. 게다가 앞서 말했듯이 그러한 행동이 자신에게 얼만큼의 효용을 가져다 줄지도 고려한다. 그래서 대개 결정 이론(decision theory)은 확률 이론(probability theory)과 효용 이론(utility theory)을 함께 고려한다. Utility에 관한 내용은 추후 utility와 decision network 글에서 자세히 설명할 계획이다.
$$\text{Decision Theory = Utility Theory + Probability Theory}$$
어떤 불확실성을 지닌 문제에 관해 행동을 결정할 때는 확률을 고려할 뿐만이 아니라 효용도 고려한다.
Evidence

앞서 우리는 공항에 도착하기까지 30분이 걸린다고 알고 있었다. 그런데 네비게이션 앱으로 예상 소요 시간을 확인해 보니 교통 체증으로 인해 1시간 30분이 걸린다고 한다. 그러면 과연 이전에 공항으로 세 시간 전에 출발하는 행동이 과연 이전처럼 가장 바람직한 결정이 될 수 있을까? 제 시간에 이륙편에 탑승할 수 있는 확률이 달라지므로 장담할 수 없다.
이처럼 우리가 문제에 관하여 어떠한 행동을 하기 전에 새로운 정보를 알게 되면 기존에 알고 있던 정보가 달라질 수 있다. 이때 기존의 알고 있는 정보를 달라지게 할 수 있는 주어진(given) 정보를 증거(evidence)라고 한다. 우리는 앞으로 이 evidence에 주목하려고 하는데, 왜냐하면 앞서 말했듯이 이 evidence가 기존에 알고 있던 정보를 바꿀 수 있기 때문이다. 참고로 이 evidence가 주어졌을 때 어떠한 사건이 발생할 확률을 사후확률이라고 하는데, 이는 베이즈 정리에서 자세히 다룰 것이다.
앞으로 evidence와 given이라는 말을 자주 연관지어 사용하는데, '어떤 사건 $A$가 given인 상황'이라는 말은 '어떤 사건 $A$가 evidence로 주어졌을 때'라고 이해해도 된다.
Evidence가 주어지면(given) 기존에 알고 있던 정보를 달라지게 할 수 있으므로, 앞으로 evidence에 유의해서 보자.
확률과 사건
먼저 사건에 관한 수학적 정의를 소개하고, 예시를 통해 확률과 사건에 관한 정의를 이해해 보고자 한다.
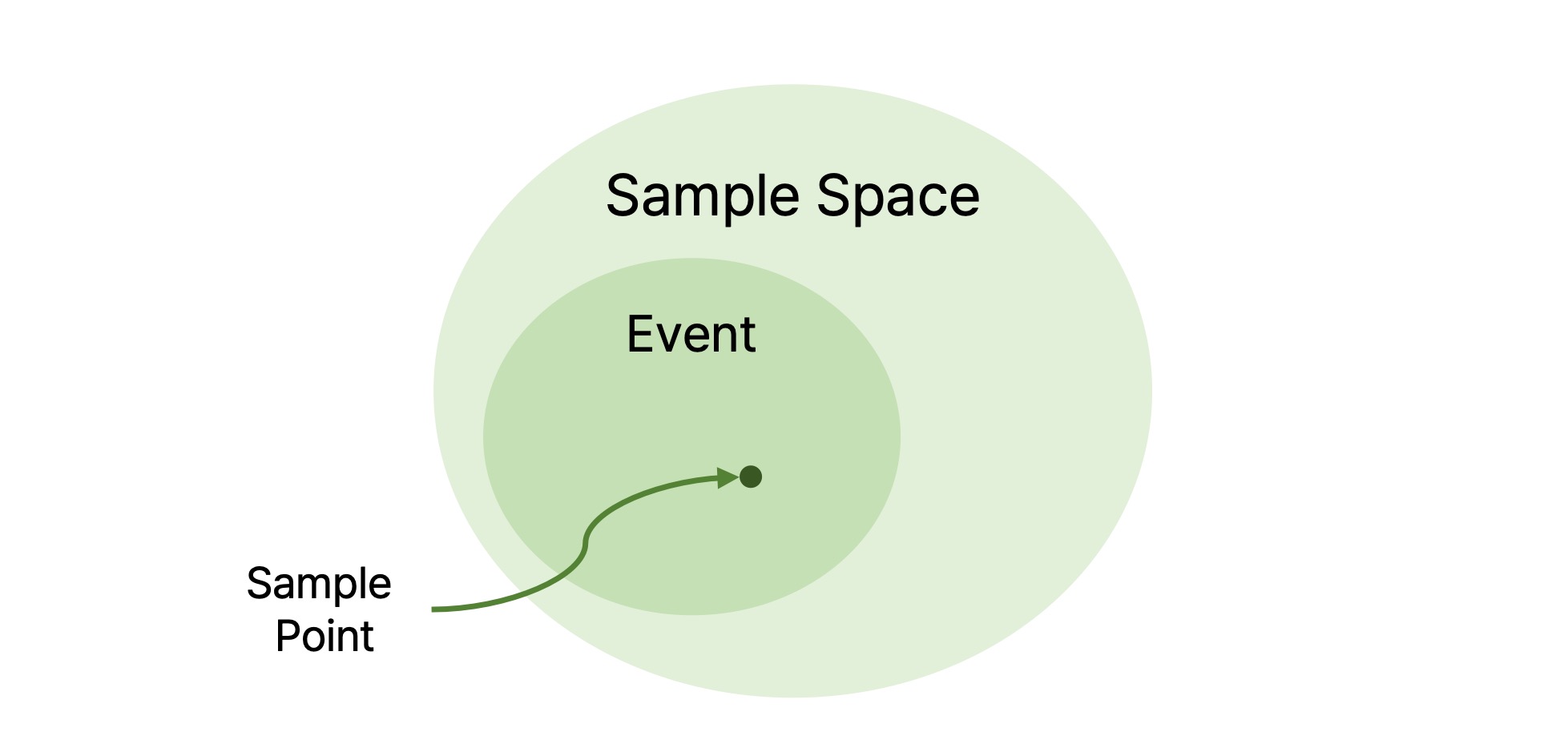
어떠한 사건 $A$가 발생할 확률이 $P(A)$라고 할 때, 그 사건 $A$는 sample point인 $\omega$의 집합이고 가능한 모든 sample point의 집합이 표본 공간(sample space) $\Omega$이다.
즉, 사건 $A$는 표본 공간 $\Omega$의 부분집합이므로 사건 $A$에 속하는 sample point $\omega$에 관한 확률 $P(\omega)$를 모두 합한 값이 바로 사건 $A$에 관한 확률 $P(A)$이다. 이를 수식으로 정리하면 다음과 같이 쓸 수 있다.
확률 공간(probability space) 또는 확률 모델(probability model)은 표본 공간의 일종인데, 표본 공간 $\Omega$에 속하는 모든 sample point $\omega$가 다음과 같은 조건을 만족해야 한다.
다시 말해, 확률 공간을 구성하는 각각의 sample point에 관한 확률이 0 이상 1 이하여야 하고, 그 모든 확률의 합이 1을 만족하면 되는 것이다.
6개의 면에 1부터 6까지 숫자가 적힌 주사위 한 개를 굴리는 경우를 생각해 보자. 그러면 주사위를 굴렸을 때 나오는 1부터 6까지 각각의 모든 숫자가 sample space를 구성한다. 그리고 그 각각의 숫자는 표본 공간을 구성하는 원소인 sample point로 볼 수 있다. 또한 확률 공간 또는 확률 모델은 주사위를 굴렸을 때 1부터 6까지 각각의 숫자가 나올 확률이 0 이상 1 이하이고 이 모든 숫자의 확률의 합이 1과 같은 표본 공간으로 볼 수 있다.
사건(event) = sample point의 집합
표본 공간(sample space) = 사건의 집합 = sample point의 집합
확률 공간(probability space) = 각 sample point 확률이 0 이상 1 이하, 모든 sample point 확률의 합이 1인 표본 공간
사건과 Sample Point의 차이
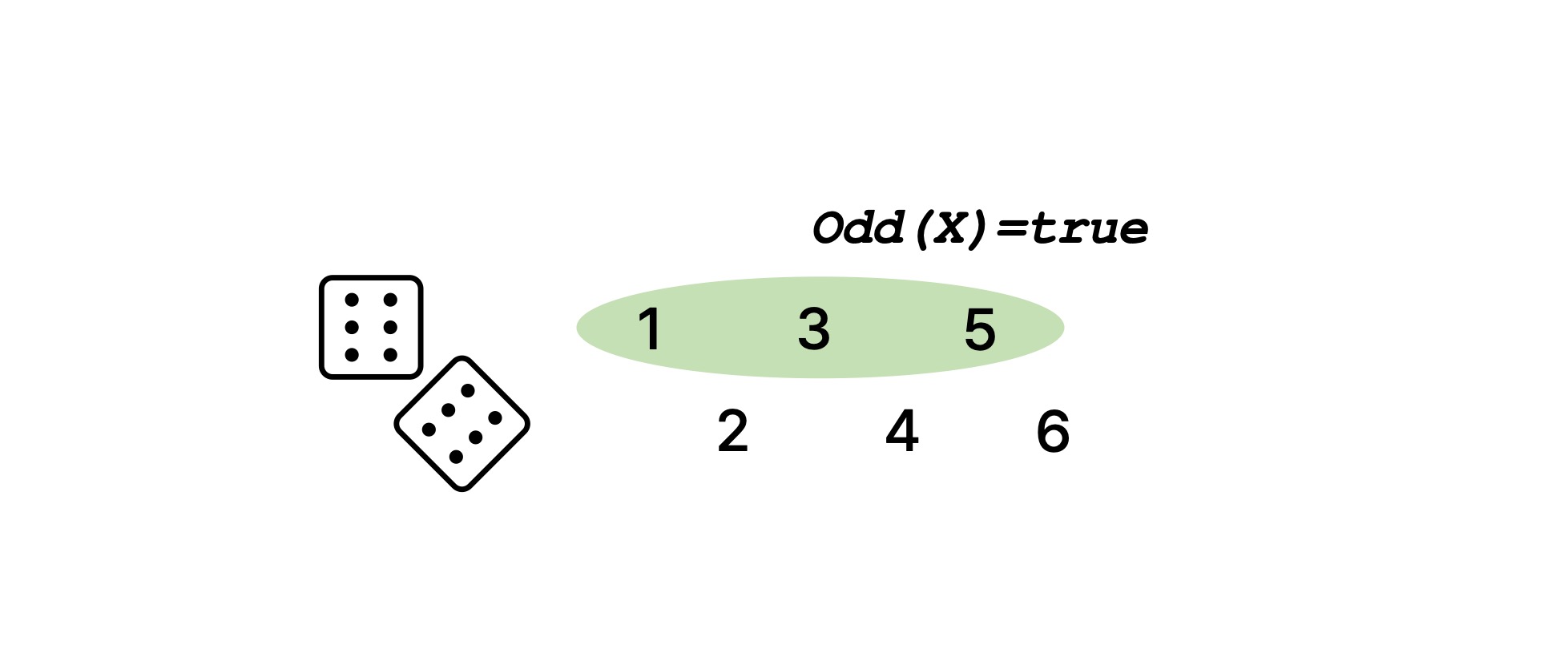
그러면 사건과 sample point의 차이가 헷갈릴 수도 있을 텐데, 사건은 앞서 설명한 바처럼 sample point의 집합이다. 주사위를 예로 다시 들어 보자. 주사위를 던졌을 때 나온 수 $X$가 홀수인 사건을 $Odd(X) = true$라고 하면, 이 사건은 주사위가 1, 3, 5로 나오는 sample point를 모두 합한 것이다. 즉, $P(Odd(X) = true)$는 $P(1) + P(3) + P(5)$와 같다.
확률과 명제(Proposition)
랜덤 변수(Random Variable)
앞서 말한 사건을 랜덤 변수(random variable)와 연관지을 수도 있다. 랜덤 변수는 sample point를 정의역으로 갖고 어떠한 범위(some range)를 치역으로 가지는 함수로 정의할 수 있는데, sample point를 어떠한 범위로 mapping시키는 함수인 것이다. 앞서 말한 $Odd(X)$를 랜덤 변수라고 볼 수 있는데, 주사위를 던질 때 나오는 수 1, 3, 5에 관한 sample point를 $Odd$라는 함수에 통과시키면 $true$라는 boolean 값을 반환하는 함수임을 확인할 수 있다.
사건과 명제
그러면 왜 지금까지 사건과 랜덤 변수에 관해 설명했는지 의아해 할 수 있다. 이는 AI를 사용할 때 '명제(proposition)'를 자주 사용해서인데, 명제와 First Order Logic에 관한 자세한 설명은 추후 인공지능 시리즈 글에서 이어갈 예정이다. 간단히 말해 명제는 논리학적으로 참 또는 거짓을 판단할 수 있는 문장을 의미하는데, 인공지능에서는 복잡한 사실을 여러 개의 간단한 명제로 만들어서 새로운 사실이 entailment 되는지를 판단하고 이를 처리하는 경우가 종종 존재한다. 더 자세한 내용은 First Order Logic과 추론 부분을 설명하는 글에서 상세히 설명할 계획이다.
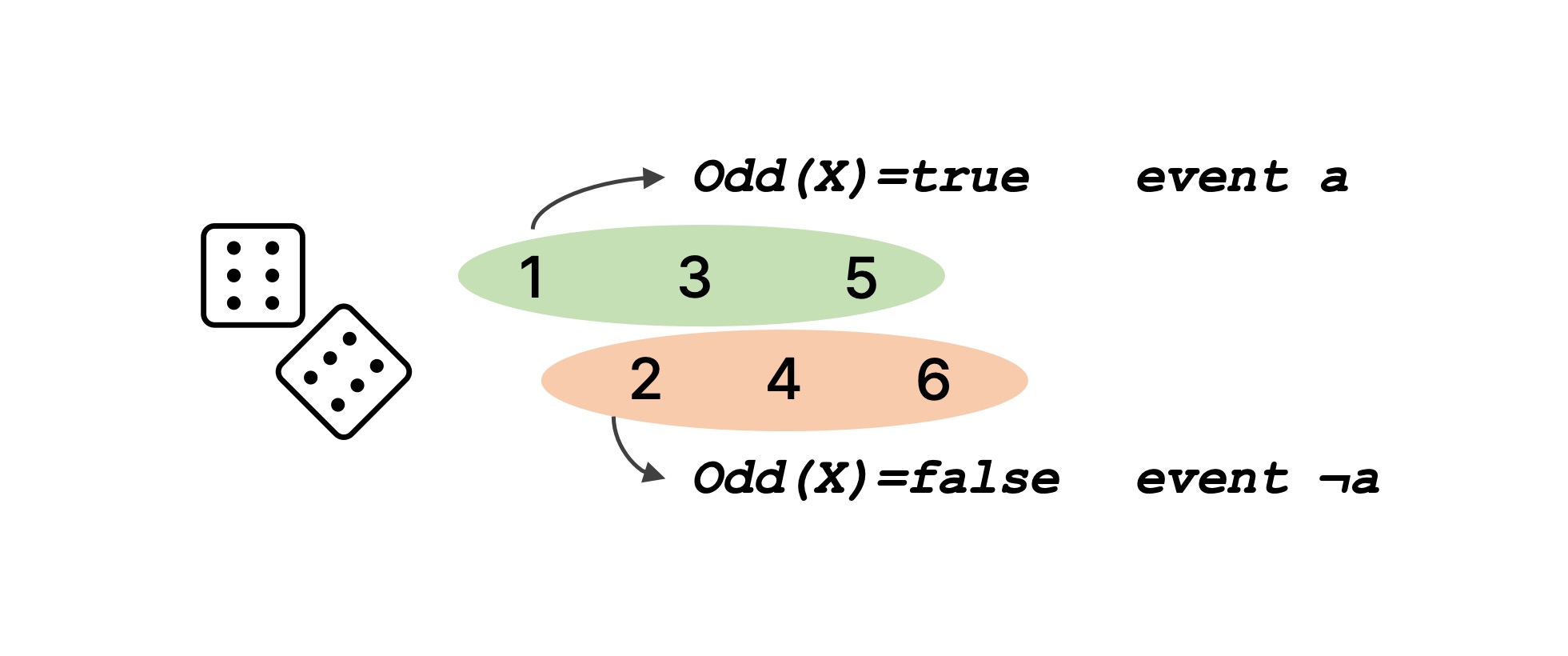
''명제가 참이다'' 또는 '명제가 거짓이다'를 사건처럼 생각하면 어떨까? 앞서 설명한 예시 중에서 주사위를 던졌을 때 나온 수 $X$가 홀수인 사건을 $Odd(X) = true$라고 보자고 했는데, 이를 사건 $a$라고 볼 수 있지 않느냐는 것이다. 그러면 $Odd(X) = false$인, 다시 말해 주사위를 던졌을 때 나온 수 $X$가 홀수가 아닌(짝수인) 경우는 사건 $\neg a$로 나타낼 수 있다. 이를 간단하게 다음 문장으로 정리해 볼 수 있을 것이다
이처럼 어떠한 사건을 명제와 부정 기호($\neg$)를 사용해서 표현하는데, 왜 사건이라는 것을 굳이 명제로 만들어서 표현하는 것일까? 우리가 사건을 하나만 다루면 모르겠지만, 실제로는 여러 사건이 동시에 발생하거나 서로 연관 관계를 파악하고자 많은 사건을 함께 고려하는 경우가 많다. 명제로 간단히 표현할 수 있으면 사건이 함께 발생하는 교집합을 고려할 수 있고, 사건의 여집합을 부정 기호($\neg$)로 간단히 표현해서 확률 계산 시 편해진다는 장점을 지니고 있다. 만약 주사위를 던졌을 때 홀수가 나오는 경우도 고려하면서 나온 숫자가 4 미만인 경우도 함께 고려해야 한다면 어떻게 될까? 주사위로 나온 숫자가 4 미만인 사건을 $b$라고 가정하면, 우리는 다음처럼 명제를 사용해 간단히 교집합으로 표현할 수 있게 된다.
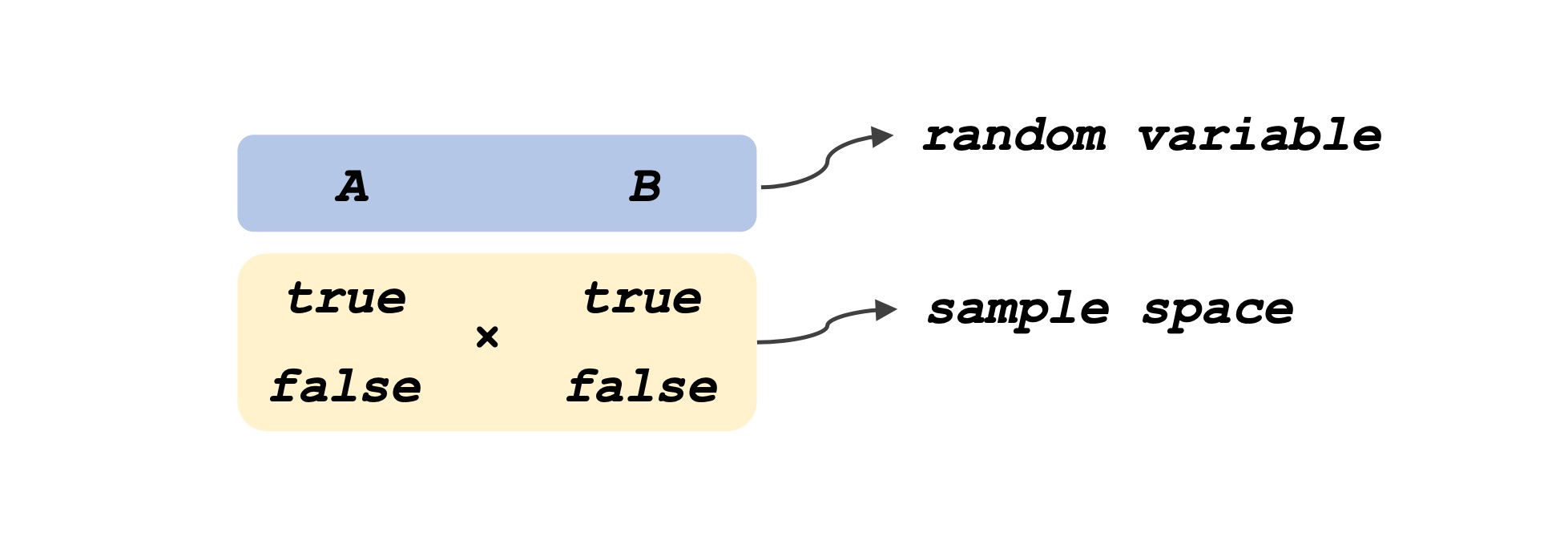
앞서 우리는 sample point 각각을 따로 고려했지만, AI에서는 일반적으로 sample point들을 랜덤 변수들의 값들의 집합으로 표현한다. 즉, 우리는 sample point 자체가 무엇인지는 크게 관심이 없고 랜덤 변수가 어떠한 값을 지니는지를 보겠다는 것이다. 위의 주사위를 던지는 예시에서 랜덤 변수를 $Odd$와 $SmallerThan4$라고 했는데, 이제부터 이를 간단하게 각각 랜덤 변수 $A$와 $B$로 표현해 보자. 사건 $a$는 $A = true$와 같고, 사건 $b$는 $B = true$와 같으며, $\neg a$는 $A = false$, $\neg b$는 $B=false$와 같다. 또한 각각의 랜덤 변수 $A$와 $B$는 $\left\{ true, false \right\}$ 중 하나의 값을 지닐 수 있다. 그러면 sample space는 각각의 랜덤 변수가 지닐 수 있는 값들의 Cartesian product로 볼 수도 있지 않을까? 즉, 랜덤 변수가 지닐 수 있는 값들의 온갖 combination이 될 것이다. 앞의 예시에서는 랜덤 변수 $A$와 $B$가 지닐 수 있는 값의 범위가 $\left\{ true, false \right\}$이므로 sample space는 $\left\{ \left( true, true \right), \left( true, false \right), \left( false, true \right), \left( false, false \right) \right\}$이다.
이제 여러 사건에 관해 명제를 통해 간단히 표현할 수 있다. 사건 $a$가 일어나거나 사건 $b$가 일어나는 경우, 즉 $a$와 $b$ 중 최소한 하나의 사건이 발생하는 경우는 합집합(disjunction)을 사용하여 $a \vee b$로 나타낼 수 있다. 모든 합집합은 교집합(conjunction)의 합집합으로 표현할 수 있으므로 다음과 같이 정리할 수 있다.
사건 $a$ 또는 $b$가 일어날 확률을 구한다면 위의 식에서 각 항을 확률을 의미하는 기호인 $P$로 감싸주면 된다. 일반적으로 확률의 합의 법칙에 의해 각 사건에 관한 항에 대하여 교지밥을 고려해야 하지만, 위의 오른쪽 식의 각 항의 교집합이 서로 공집합이므로 교집합을 고려할 필요 없이 각 항에 관한 확률을 더해주면 된다.
랜덤 변수 = sample point를 어떠한 범위로 mapping 시키는 함수
Sample point는 크게 관심 없고, 랜덤 변수가 어떠한 값을 지니는지에 관한 사건을 명제로 표현할 것이다.
Sample space = 랜덤 변수가 지닐 수 있는 값들의 Cartesian product
랜덤 변수의 값(value)
앞서 우리는 랜덤 변수의 값이 $true$ 또는 $false$인 경우만을 고려했지만, 단순히 boolean 값만을 지니는 것이 아니라 불연속적인(discrete) 값을 지닐 수도 있다. 예를 들어, 날씨를 뜻하는 $\text{Weather}$ 랜덤 변수가 지닐 수 있는 값의 범위가 $\text{sunny}, \text{rain}, \text{cloudy}, \text{snow}$일 경우 string 형태의 불연속적인 값을 지닌다. 불연속적인 값 뿐만이 아니라 연속적인(continuous) 값을 지닐 수도 있는데, 온도를 뜻하는 $\text{Temperature}$ 랜덤 변수는 $18.4$와 같이 연속된 실수 범위에서 임의의 한 실수 값을 지닐 수 있다.
이처럼 랜덤 변수 값이 불연속적이든 연속적이든 간에 값은 반드시 완전(exhaustive)해야 하고 상호 배타적(mutually exclusive)이어야 한다. 여기서 완전하다는 건 랜덤 변수의 값이 하나로 정해졌으면 그 값이어야 한다는 것이다. 그러니까 값이 한 번 정해지면 '이것일 수도 있고 저것일 수도 있다'는 것처럼 애매해서는 안 된다는 것이다. 또한 상호 배타적이라는 것은 정해진 값이 다른 것과 의미적으로 중복되어서는 안 된다는 것이다. 비가 오는 상태인 $\text{rainy}$와 해가 뜬 상태인 $\text{sunny}$는 서로 의미적으로 겹치는 바 없이 배타적이다.
랜덤 변수는 불연속적이거나 연속적인 범위의 값을 지닐 수 있으며, 반드시 완전해야 하고 상호 배타적이어야 한다.
출처
1. 서강대학교 CSE4185 기초인공지능 양지훈 교수님 수업
2. Stuart J. Russell, Third Edition, Artificial Intelligence: A Modern Approach
'AI > AI 수학' 카테고리의 다른 글
| [빠르게 정리하는 선형대수] Eigenvalue와 Eigenvector (0) | 2023.02.21 |
|---|---|
| [인공지능 기초] Uncertainty(2) - 결합 확률과 조건부 확률 그리고 베이즈 정리 (0) | 2023.01.21 |
| 통계와 최대가능도 추정법(MLE) (0) | 2022.02.14 |
| 확률(Probability)과 딥 러닝(Deep Learning) (0) | 2022.02.14 |
| 미분과 경사하강법(Gradient Descent) (1) | 2022.02.14 |
소중한 공감 감사합니다.