딥 러닝에서의 일반화(Generalization)와 최적화(Optimization)
- -
Generalization
학습된 모델이 다른 새로운 데이터에 관해서도 잘 작동하도록 하는 것이 일반화이다.
학습 Iteratiion이 늘어남으로 인해 무조건 training error가 낮아진다고 해서 test error도 낮아진다는 보장이 없다.
Generalization Gap
Training error와 test error의 차이로 인해 실제 테스트 결과가 검증 결과와 차이가 생기는 것이다.
Overfitting
모델이 학습 데이터에 관해서만 너무 학습되어서 예측률이 떨어져서 새로운 데이터에 관해서는 좋은 결과를 보이지 못하는 현상이다.
Underfitting
Network가 단순하거나 일반화에 너무 치중한 나머지 모델이 학습 데이터에 관해 덜 학습된 현상이다.
Cross-validation
데이터를 train data와 validation data를 나눠서 모델에 적용하는 테크닉이다.
단순히 이를 50:50으로 나누는 것보다는 k-fold validation처럼 데이터를 $k$개로 나누어서 $k-1$개는 train data로, 나머지 1개는 validation data로 설정할 수 있다.
Cross-validation을 해서 최적의 hyperparameter set을 찾고, 구한 최적의 hyperparameter를 고정하여 모든 데이터 셋을 다 학습시키는 게 유리하다.
test data는 어떤 방법으로든 모델의 학습에 사용되어서는 안 된다.
Bias and Variance
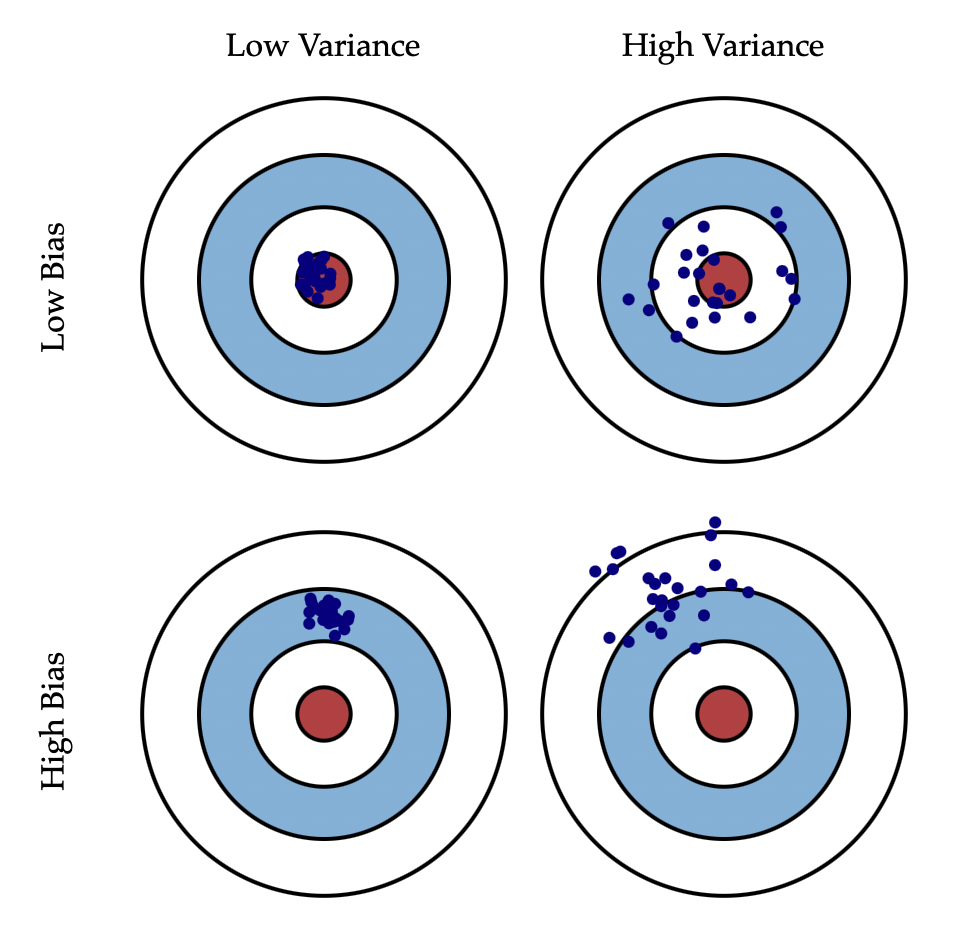
[출처] https://scott.fortmann-roe.com/docs/BiasVariance.html, Scott Fortmann-Roe
- Bias: 예측값들과 정답과의 차이
- Variance: 예측값들끼리의 차이
Variance는 비슷한 입력을 넣었을 때 출력이 얼마나 일정한지를 의미한다.
예를 들어, 총알을 여러 발 쏘았을 때 탄착군을 형성하면 그 위치만 target으로 옮기면 되므로 좋다고 한다.
Bias는 출력이 많이 분산되더라도 평균적으로 고려했을 때 우리가 원하는 target에 얼마나 가까운지를 의미한다.
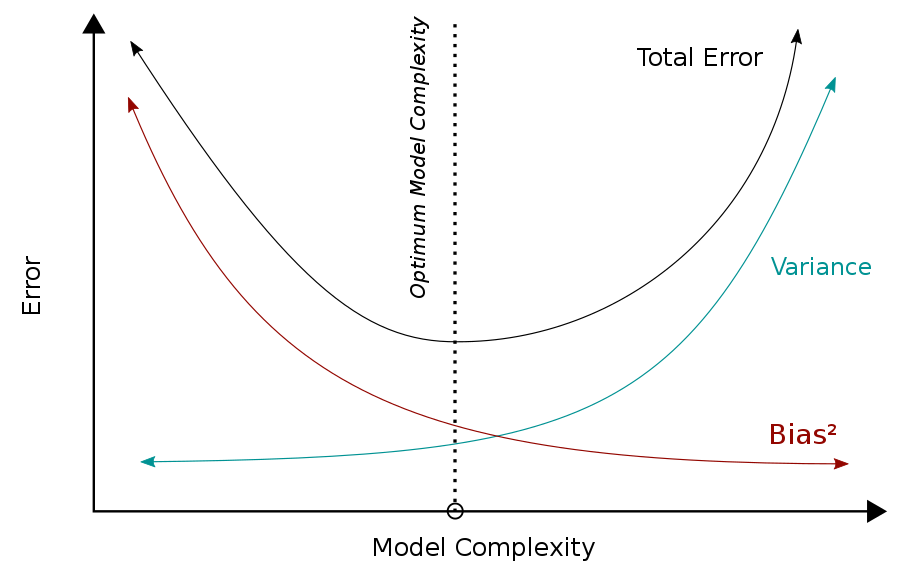
Cost를 최소화하는 건 세 가지 부분으로 나뉠 수 있다.
bias가 높아지면 variance가 낮아질 거이고, variance가 높아지면 bias가 낮아질 것이다.
근본적으로 학습 데이터에 noise가 껴 있을 경우 Neural Network 모델에서 bias와 variance를 둘 다 낮추는 것은 어렵다. (편향-분산 트레이드오프)
Bootstrapping
학습 데이터 중 일부만 사용해서 학습한 모델을 여러 개 만들었을 때, 이 각각의 모델이 모두 비슷한 값을 예측할 수 있지만 다른 값을 예측할 수도 있다. 이 모델들의 예측에 관한 consensus를 보고, 전체적인 모델의 uncertainty를 파악하고자 할 때 사용한다.
아래 포스트에서 부트스트랩에 관한 자세한 내용이 정리되어 있어서 도움이 되었다.
https://mingchin.tistory.com/316
[딥러닝/DL Basic] 최적화(Optimization) 관련 용어 정리 (1)
1) Generalization(일반화, 일반화 성능) Train data에 대한 성능과 Test data(혹은 validation data)에 대한 성능의 차이를 말한다. 둘 간의 차이가 작을수록 학습 데이터 뿐만아니리 Test data에 대해서도 모델..
mingchin.tistory.com
Bagging(Bootstrapping Aggregating)
bootstrapping으로 여러 모델을 만들고, 이 모델들을 가지고 전체 output의 평균을 구하거나 또는 voting을 하는 앙상블 기법의 일종이다.
Boosting
[출처] Wikipedia, Sirakorn
학습 데이터를 sequential한 관점으로 바라보는데, 우선 모델을 간단하게 하나를 만들어 보고 이를 일부 학습 데이터로 학습시킨다. 그 다음 두 번째 모델은 앞에서 잘못 예측한 데이터에 집중하여 학습시킨다. 이렇게 만들어진 모델을 weak learner라고 한다.
이를 통해 여러 개의 모델을 만들어서 각 모델별로 가중치를 계산하여 합치는데, 이를 독립적인 결과로 보는 게 아니라 weak learner를 모아서 하나의 strong learner를 구축한다.
정리하면, 특정 train data에 집중하는 weak learner들을 만들고, weak learner들을 sequential하게 합쳐 strong model을 만드는 방식이다.
Gradient Descent Methods
Stochastic Gradient Descent
Single Sample만 사용해서 gradient를 업데이트 하는 기법이다.
Mini-batch Gradient Descent
Batch size만큼의 sample만 사용해서 gradient를 업데이트 하는 기법이다.
Batch Gradient Descent
모든 데이터를 사용해서 gradient를 업데이트 하는 기법이다.
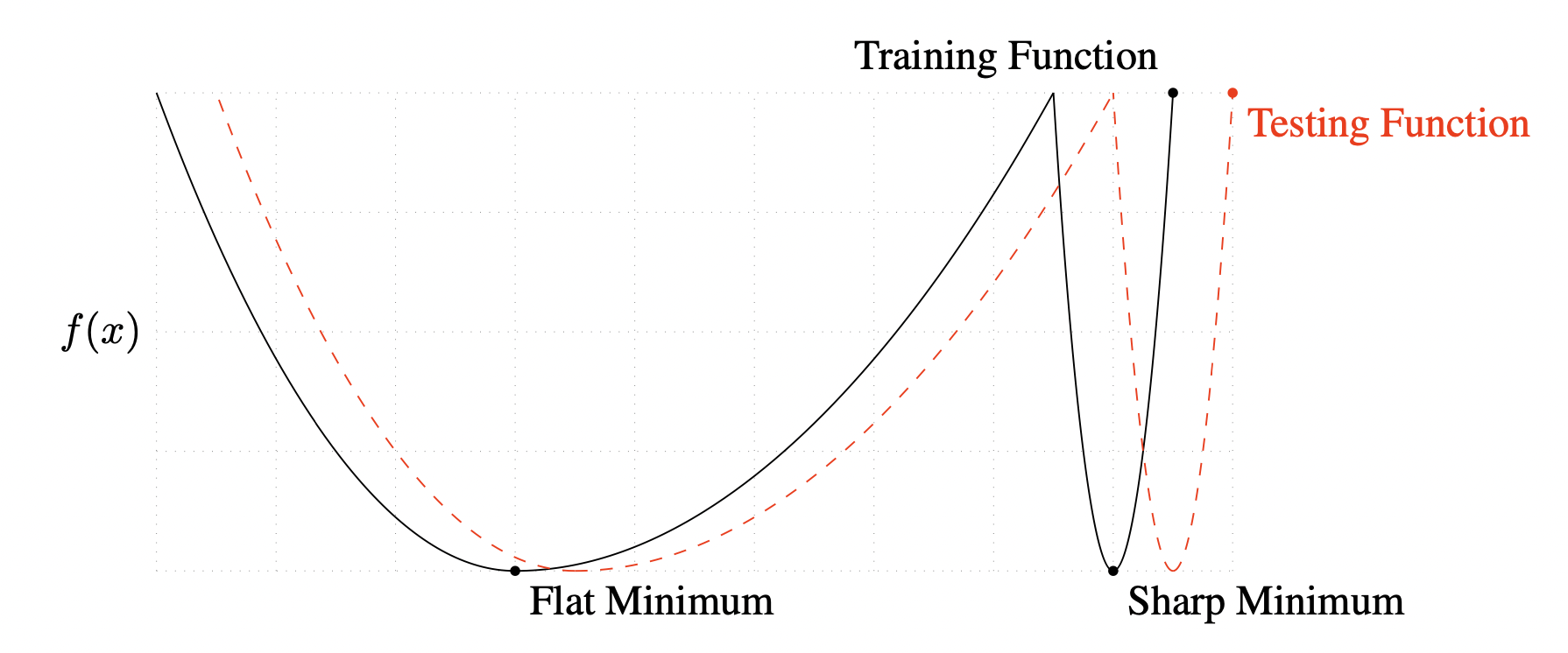
[출처] https://arxiv.org/pdf/1609.04836.pdf, ON LARGE-BATCH TRAINING FOR DEEP LEARNING: GENERALIZATION GAP AND SHARP MINIMA
Sharp minimum은 flat minimum보다 손실함수가 상대적으로 더 뾰족한 형태이고, train할 때의 loss와 test할 때의 loss의 차이가 큰 optimal에 수렴할 가능성이 높다.
그래서 Flat Minimizer는 Generalization Performance가 좋지만, Sharp Minimizer는 그렇지 않을 수 있다.
그런데 batch size가 커지면 sharp minimum에 도달할 가능성이 높아지고, 반대로 batch size가 작아지면 flat minimum에 도달할 가능성이 높아진다.
그래서 일반적으로 batch size를 줄이면 Generalization Performance가 좋아지는 경향이 있다는 내용이 논문에서 제안되었지만, 이에 관한 논란이 꽤 있으며 실제로 batch size를 크게 하면 최종 모델의 성능이 높아진다는 주장도 적지 않다.
또한 batch size와 일반화 성능의 관계를 다른 관점으로도 해석할 수 있는데, batch size를 파라미터를 업데이트하는 횟수와 연관지어 고려하는 것이다.
Learning rate는 파라미터를 업데이트할 때의 보폭(이동 크기), batch size는 파라미터를 얼마나 업데이트할 것인지 그 횟수에 반비례하는 값으로 생각해 볼 수 있다.
이때 learning rate를 고정하게 되면, batch size가 커질수록 파라미터를 업데이트하는 횟수가 줄어드므로 덜 학습될 가능성이 높아진다.
반대로 batch size가 작아질수록 파라미터를 업데이트하는 횟수가 많아지므로 더 학습될 가능성이 있다.
그러나 반드시 파라미터 업데이트 횟수가 적다고 해서 덜 학습되어 손실함수의 극소를 찾을 수 있다는 보장은 없다.
파라미터 업데이트 횟수가 증가하여 더 많이 이동해서 결과적으로 minimum을 빠져나갈 수도 있으므로, 적절히 작은 batch size를 고려하는 것이 바람직하다.
이는 batch size 관점에서만 고려한 내용이고, 실제로는 다양한 하이퍼퍼라미터를 고려하여 tuning하는 것이 바람직하다.
Optimizer
Gradient Descent
Gradient Descent의 단점은 적절한 learning rate(step size)와 step의 방향을 찾는 게 어렵다는 것이다.
Momentum
Gradient Descent의 단점을 보완할 수 있는 기법이다.
직관적으로 관성처럼 gradient 방향이 바뀌어도 원래 흐르던 방향의 데이터를 활용해 보자는 아이디어에서 나온 것이다.
이전에 계산된 gradient를 현재 단계에서도 이용하는 방식이며, 한 번 흘러가기 시작한 gradient 방향을 어느 정도 유지시켜 학습이 잘 되도록 유지시킨다.
$a$는 momentum인 $\beta$의 정보를 갖고 있는 accumulated gradient이다.
Nesterov Accelerated Gradient(NAG)
Momentum 기법과 유사한데, accumulated gradient를 계산할 때 lookahead gradient를 사용한다.
원래 momentum은 현재 주어진 파라미터에서 gradient를 계산하고, 그 gradient를 가지고 momentum을 optimize한다.
그래서 momentum에 의해 local minimum에 수렴하지 못하는 현상이 생긴다.
NAG는 momentum 방향으로 momentum step만큼 한 번 이동하고 거기서 accumulated gradient를 구하는 것이다.
즉, 관성 방향으로 우선 움직이고, 그 자리에서 최적의 step을 계산하는 것이다.
Adagrad
Neural network 모델의 파라미터가 지금까지 얼마나 많이 변했는지를 확인한다.
그래서 지금까지 많이 변한 파라미터는 적게 변화시키고, 적게 변한 파라미터는 많이 변화시키는 기법이다.
$G_t$(Sum of gradient squares)는 지금까지 각 파라미터가 얼마나 변했는지를 갖고 있다.
$\epsilon$은 0으로 나누는 걸 방지하기 위한 Numerical stability 요소이다.
Adagrad의 단점은 $G_t$가 계속 커져서 파라미터의 학습이 멈춰지는 현상이 발생할 수 있다는 것이다.
Adadelta
Adagrad의 단점인 $G_t$가 계속 커지는 현상을 막기 위해 이전의 모든 timstep에 관해서가 아니라 window size만큼의 시간동안 $G_t$의 변화를 보는 것이다.
Adadelta는 learning rate가 없다는 게 특징이어서 많이 사용되지는 않는다.
RMSprop
Geoff Hinton이 딥러닝 강좌를 진행하다가 자신의 경험을 바탕으로 제안한 기법이다.
Adagrad에서 문제점을 개선하기 위해 $G_t$의 계산식에 EMA(Exponentail Moving Average, 지수 이동 평균)를 적용했다.
Adadelta에서 다시 학습률을 적용시킨 방식이며, 이전까지 변화한 파라미터의 상황을 반영하여 step size를 업데이트 하는 것이다.
$G_t$는 gradient squares의 EMA(Exponentail Moving Average, 지수 이동 평균)이고, $\eta$는 step size이다.
Adam (Adaptive Moment Estimation)
Gradient Squares를 사용함과 동시에 momentum을 같이 활용하는 기법이다.
그래서 Momentum과 RMSprop의 장점을 동시에 반영했다고 볼 수 있다.
이전의 gradient와 gradient의 제곱합을 동시에 활용한다.
$m_t$는 momentum, $v_t$는 gradient squares의 EMA(Exponentail Moving Average, 지수 이동 평균)이다.
일반적으로 자주 사용되고, 성능이 좋다고 알려져 있는 기법이다.
Regularization
학습을 방해하도록 규제하여 학습 데이터뿐만이 아니라 테스트 데이터에도 동작을 잘 하도록 한다.
Early Stopping
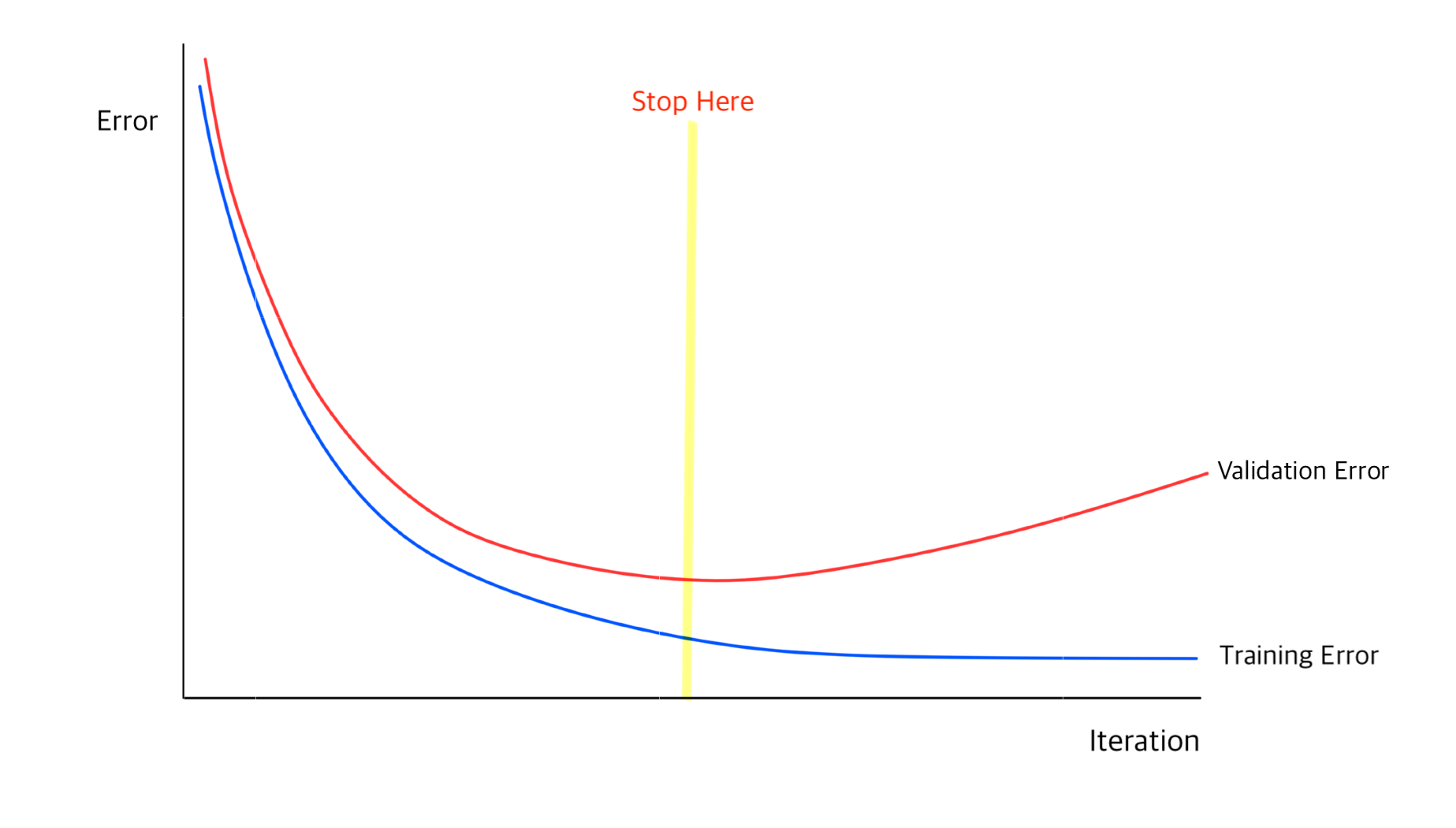
Validation data를 사용하여 Validation loss가 커지기 시작하는 시점에 모델 학습을 멈춰서 overfitting을 방지하는 기법이다.
Parameter Norm Penalty
Neural network 파라미터의 절댓값이 너무 커지지 않도록 막아서 function space를 부드럽게 한다.
Data Augmentation
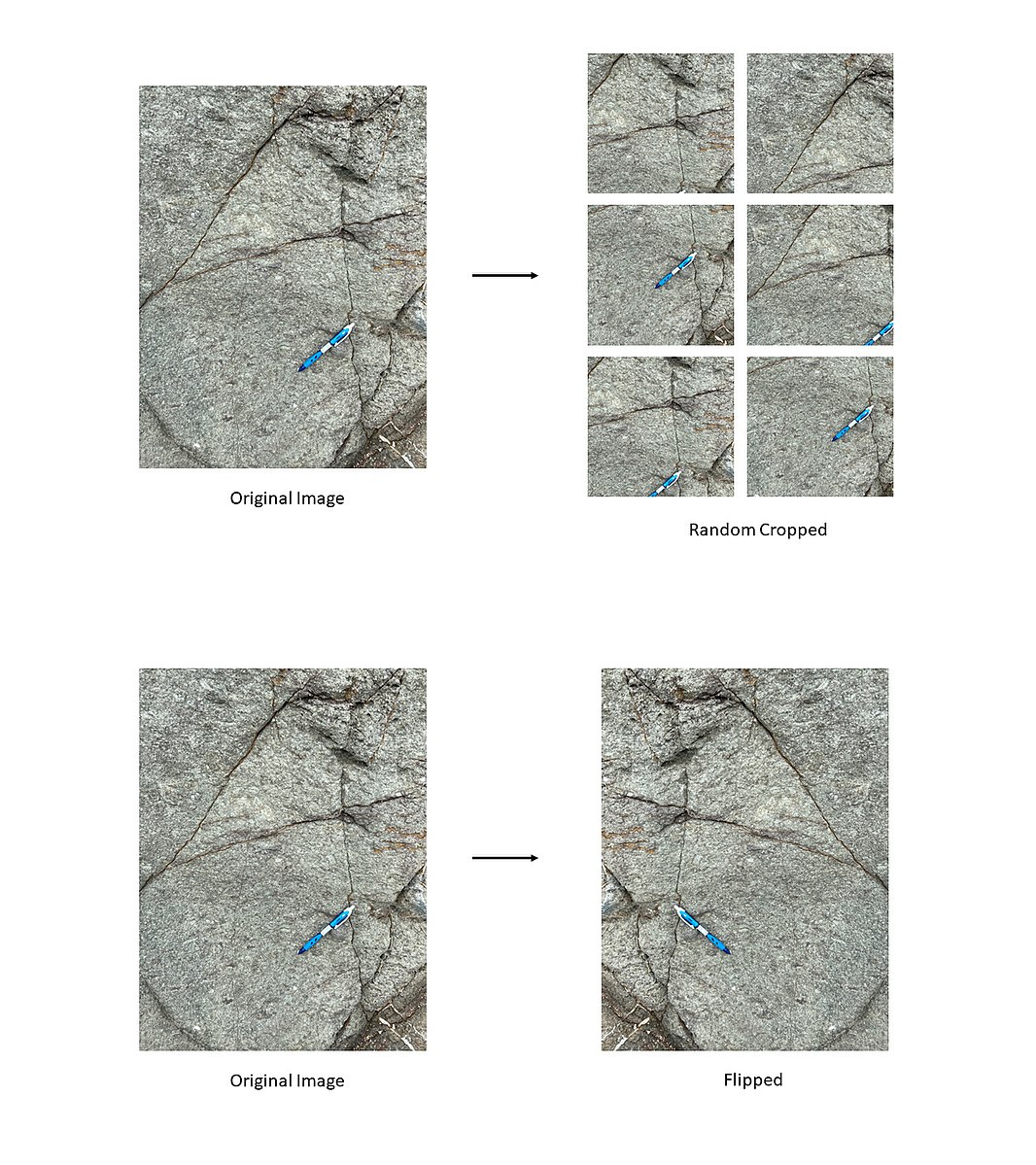
[출처] https://commons.wikimedia.org/wiki/File:Data_Augmentation_of_rock_images_revised.jpg, TseKiChun
데이터 셋의 크기가 어느 정도 커지게 되면 Deep Learning이 Neural Network이나 Traditional Machine Learning보다 더 좋은 성능을 낸다.
그러나 데이터 셋이 한정되어 있으므로, 데이터의 일부를 한도 내에서 변형하여 학습 데이터를 증가시키는 기법이다.
예를 들어, 이미지를 회전시키거나 크기를 또는 비율을 변경시키는 것이다.
Noise Robustness

Noise를 단순히 input 데이터에 넣는 것뿐만이 아니라 weight, bias 등 파라미터에도 noise를 넣을 수 있다.
Label Smoothing

학습 데이터 두 개 이상을 뽑아서 혼합하여 decision boundary를 부드럽게 만들어 주는 기법이다.
Mixup, Cutout, CutMix 등이 존재한다.
예를 들어, 학습 데이터에 해당되는 이미지와 그 라벨을 섞는 것이다.
아니면 데이터의 불균형을 해결하기 위해 기존의 label의 기준치를 조금씩 이동하는 것도 label smoothing의 일종으로 볼 수 있다.
Dropout
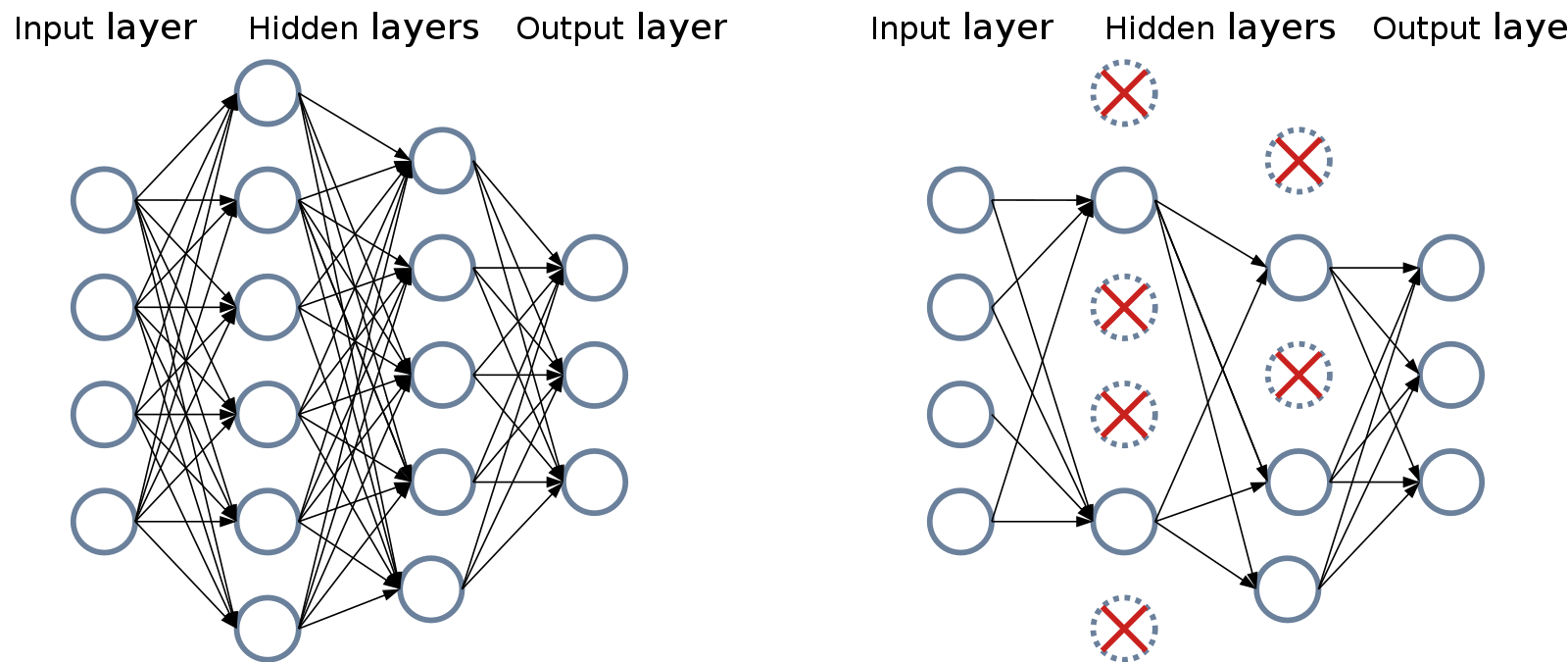
[출처] https://commons.wikimedia.org/wiki/File:Neural_Network_Dropout.svg, Mads Dyrmann
Forward pass를 할 때, 일부 neuron의 parameter를 0으로 초기화하여 일반화된 데이터에도 robust한 모델을 만드는 방식이다.
Batch Normalization
Batch Normalization을 적용하려는 layer의 statistics를 정규화시키는 것이다.
어떤 한 레이어의 파라미터 값의 변화가 모델의 결과에 미세한 변화를 미치게 되면 파라미터를 효과적으로 학습할 수 없기 때문에 배치 정규화를 수행한다.
Neural network의 layer에 속한 파라미터를 해당 레이어의 모든 파라미터의 평균을 빼주고 분산으로 나눠주는 것이다.
해당 개념을 소개한 논문에서는 Internal Covariance Shift가 학습에서 불안정을 일으킨다고 주장하지만, 다른 논문에서는 Internal Covariance Shift를 줄여서 학습을 잘 시킨다고 한 부분에서 논란이 있다.
여기서 Internal Covariance Shift는 이전 레이어의 파라미터 변화로 인해 다음 라에이어의 입력의 분포가 바뀌면서 전체적으로 모델의 각 layer마다 입력값의 분산이 달라지는 현상을 의미한다.
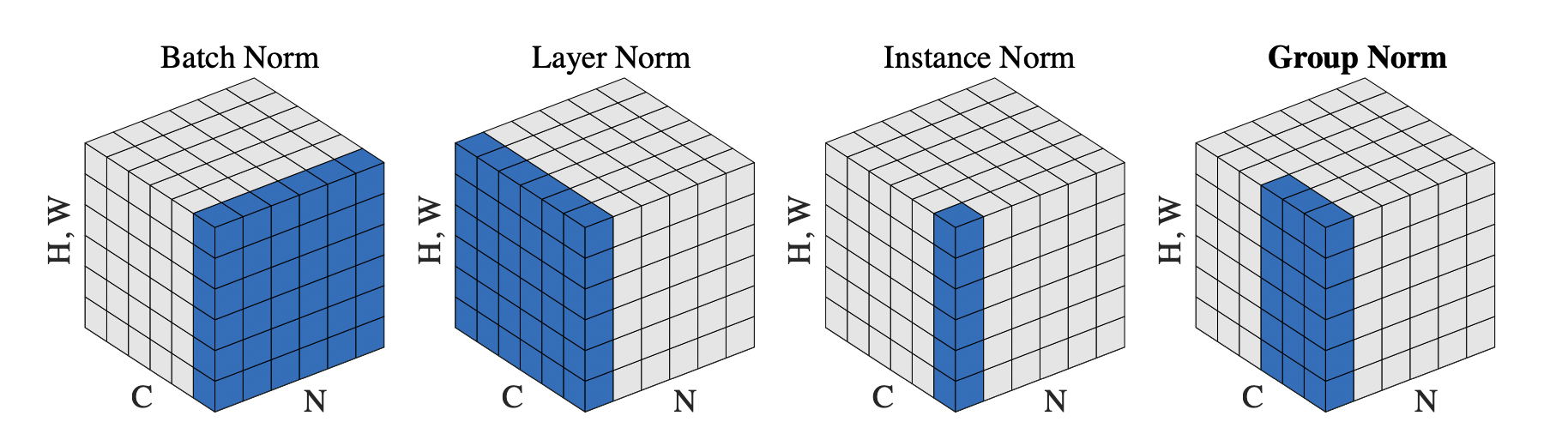
[출처] https://arxiv.org/pdf/1803.08494.pdf, Group Normalization
Batch Norm, layer norm, instance norm, group norm 등 테크닉이 있다.
Optimizer 종류에 따른 예측값의 Target으로의 수렴 속도
모델에 사용한 Optimizer에 종류에 따라 예측 결과가 실제 결과에 어느 정도의 빠르기로 얼만큼 수렴해가는지를 실험한 것이다.
Dataset 생성
n_data = 10000
x_numpy = -3+6*np.random.rand(n_data,1)
y_numpy = np.exp(-(x_numpy**2))*np.cos(10*x_numpy) + 3e-2*np.random.randn(n_data,1)
plt.figure(figsize=(8,5))
plt.plot(x_numpy,y_numpy,'r.',ms=2)
plt.show()
x_torch = torch.Tensor(x_numpy).to(device)
y_torch = torch.Tensor(y_numpy).to(device)
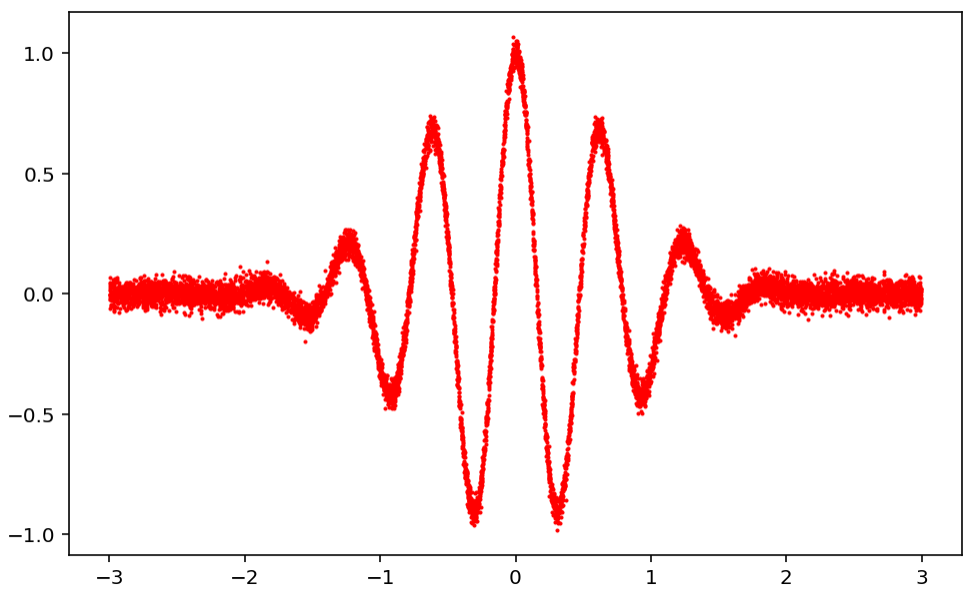
Model 정의
class Model(nn.Module):
def __init__(self,name='mlp',xdim=1,hdims=[16,16],ydim=1):
super(Model, self).__init__()
self.name = name
self.xdim = xdim
self.hdims = hdims
self.ydim = ydim
self.layers = []
prev_hdim = self.xdim
for hdim in self.hdims:
# 선형 함수
self.layers.append(nn.Linear(
prev_hdim, hdim, bias=True
))
# 활성화 함수
self.layers.append(nn.Tanh())
prev_hdim = hdim
# Final layer (without activation)
self.layers.append(nn.Linear(prev_hdim,self.ydim,bias=True))
# layer들을 sequential하게 이어준다.
self.net = nn.Sequential()
for l_idx,layer in enumerate(self.layers):
layer_name = "%s_%02d"%(type(layer).__name__.lower(),l_idx)
self.net.add_module(layer_name,layer)
self.init_param()
def init_param(self):
for m in self.modules():
if isinstance(m,nn.Conv2d): # init conv
nn.init.kaiming_normal_(m.weight)
nn.init.zeros_(m.bias)
elif isinstance(m,nn.Linear): # init dense
nn.init.kaiming_normal_(m.weight)
nn.init.zeros_(m.bias)
def forward(self,x):
return self.net(x)
Set optimizers
LEARNING_RATE = 1e-2
# Instantiate models
model_sgd = Model(name='mlp_sgd',xdim=1,hdims=[64,64],ydim=1).to(device)
model_momentum = Model(name='mlp_momentum',xdim=1,hdims=[64,64],ydim=1).to(device)
model_adam = Model(name='mlp_adam',xdim=1,hdims=[64,64],ydim=1).to(device)
# Optimizers
loss = nn.MSELoss()
optm_sgd = optim.SGD(
model_sgd.parameters(), lr=LEARNING_RATE
)
optm_momentum = optim.SGD(
model_momentum.parameters(), lr=LEARNING_RATE, momentum=0.9
)
optm_adam = optim.Adam(
model_adam.parameters(), lr=LEARNING_RATE
)
Train & check
MAX_ITER,BATCH_SIZE,PLOT_EVERY = 1e4,64,500
model_sgd.init_param()
model_momentum.init_param()
model_adam.init_param()
model_sgd.train()
model_momentum.train()
model_adam.train()
for it in range(int(MAX_ITER)):
r_idx = np.random.permutation(n_data)[:BATCH_SIZE]
batch_x,batch_y = x_torch[r_idx],y_torch[r_idx]
# Update with Adam
y_pred_adam = model_adam.forward(batch_x)
loss_adam = loss(y_pred_adam,batch_y)
optm_adam.zero_grad()
loss_adam.backward()
optm_adam.step()
# Update with Momentum
y_pred_momentum = model_momentum.forward(batch_x)
loss_momentum = loss(y_pred_momentum,batch_y)
optm_momentum.zero_grad()
loss_momentum.backward()
optm_momentum.step()
# Update with SGD
y_pred_sgd = model_sgd.forward(batch_x)
loss_sgd = loss(y_pred_sgd,batch_y)
optm_sgd.zero_grad()
loss_sgd.backward()
optm_sgd.step()
# Plot
if ((it%PLOT_EVERY)==0) or (it==0) or (it==(MAX_ITER-1)):
with torch.no_grad():
y_sgd_numpy = model_sgd.forward(x_torch).cpu().detach().numpy()
y_momentum_numpy = model_momentum.forward(x_torch).cpu().detach().numpy()
y_adam_numpy = model_adam.forward(x_torch).cpu().detach().numpy()
plt.figure(figsize=(8,4))
plt.plot(x_numpy,y_numpy,'r.',ms=4,label='GT')
plt.plot(x_numpy,y_sgd_numpy,'g.',ms=2,label='SGD')
plt.plot(x_numpy,y_momentum_numpy,'b.',ms=2,label='Momentum')
plt.plot(x_numpy,y_adam_numpy,'k.',ms=2,label='ADAM')
plt.title("[%d/%d]"%(it,MAX_ITER),fontsize=15)
plt.legend(labelcolor='linecolor',loc='upper right',fontsize=15)
plt.show()
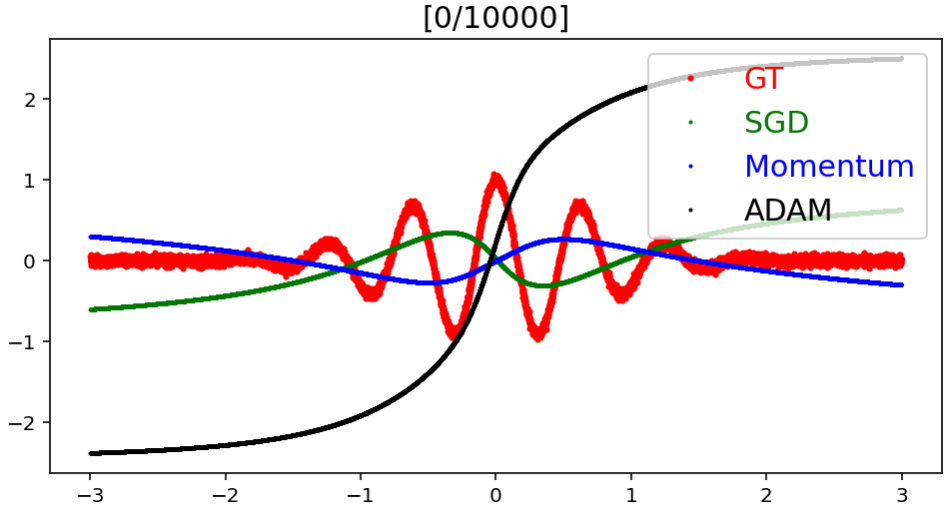
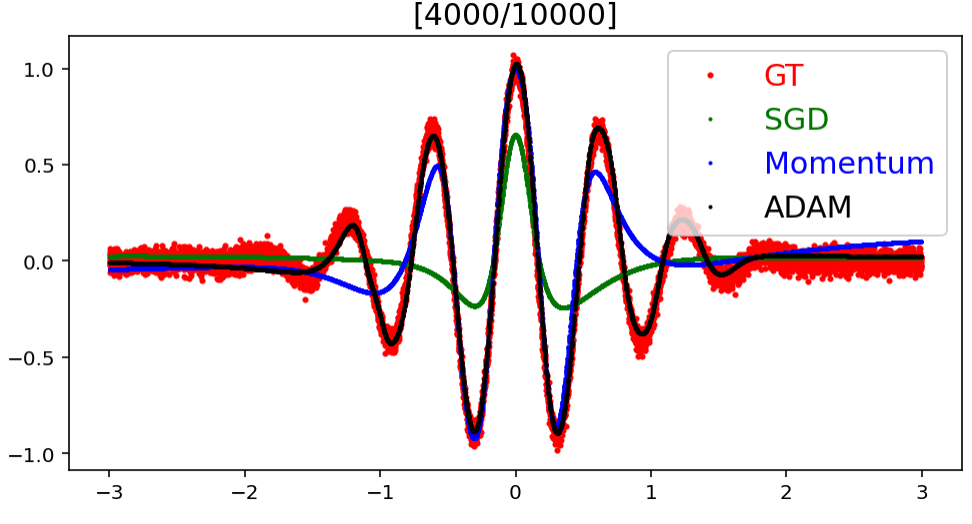
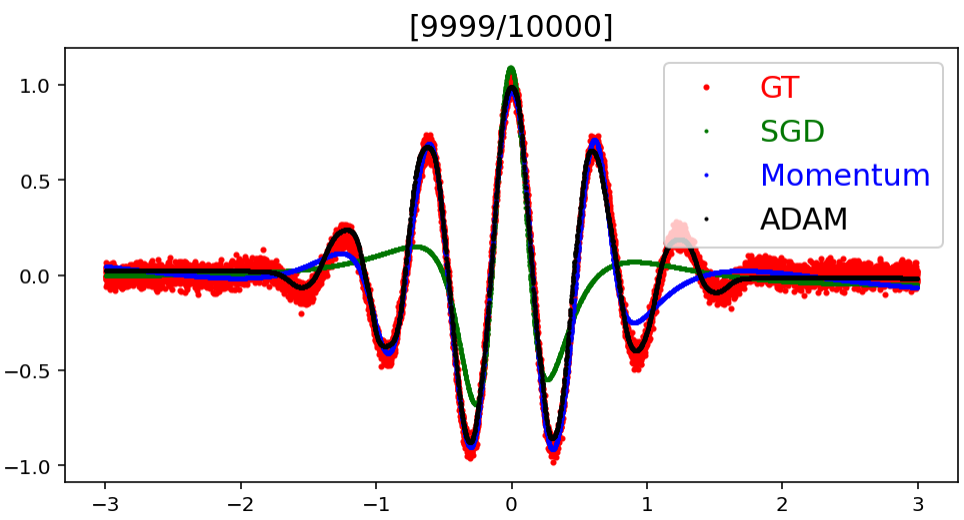
결과적으로 Adam, Momentum, SGD 순으로 target에 빠르게 수렴한다는 것을 볼 수 있으며, target과의 error도 Adam, Momentum, SGD 순으로 작다는 것을 알 수 있다.
출처
1. 네이버 부스트캠프 AI Tech Stage 1 기초 강의
2. https://mingchin.tistory.com/316
'AI > AI 기본' 카테고리의 다른 글
| Self-Attention을 사용하는 Transformer(트랜스포머) (0) | 2022.02.17 |
|---|---|
| 순차 데이터와 RNN(Recurrent Neural Network) 계열의 모델 (0) | 2022.02.17 |
| 신경망(Neural Network)과 다층 퍼셉트론(Multi Layer Perceptron) (0) | 2022.02.16 |
| 딥 러닝에서 알아두어야 할 요소와 역사적으로 중요한 모델 (0) | 2022.02.16 |
| PyTorch 딥 러닝 과정에서 자주 발생하는 문제 해결을 위한 팁 (0) | 2022.02.15 |
소중한 공감 감사합니다.
