신경망(Neural Network)과 다층 퍼셉트론(Multi Layer Perceptron)
- -
Neural Networks
Neural Networks are computing systems vaguely inspired by the biological neural networks that constitute animal brains.
- WikiPedia -
인간의 뇌를 모방해서 성능이 좋다는 게 아니라 그 모델 자체를 수학적으로 분석하는 게 바람직하다.
비행기의 발명이 새가 나는 모습을 보고 영감을 받은 건 맞지만, 비행기가 나는 원리가 새가 나는 원리와 일치한 것은 아닌 것과 유사하다.
Neural networks are function approximators that stack affine transformations followed by nonlinear transformations.
Neural Network는 행렬을 곱하는 affine transformation(아핀 변환)에다가 Activation Function(활성 함수)이라고 불리는 비선형 연산이 반복적으로 일어나는 모델이라고 정의하는 것이 좀 더 바람직하다.
여기서 아핀 변환은 $WX + b$처럼 선형 변환을 한 후 shifting이 일어나는 것이며, 엄밀히 말하면 선형 변환(선형 결합을 보존하는 두 벡터 공간을 mapping 하는 함수)은 아니지만 원하는 비선형성을 띤다고 볼 수는 없다.
선형 Neural Networks
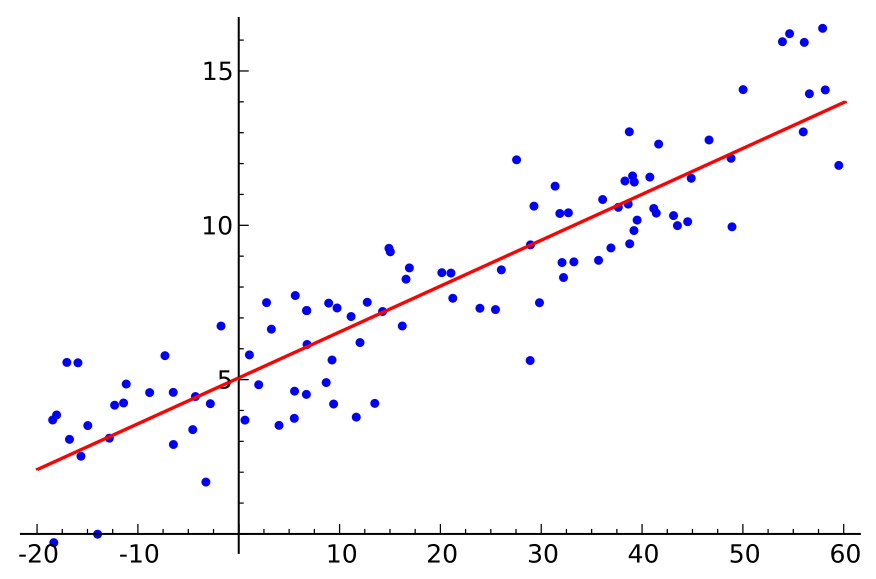
[출처] https://commons.wikimedia.org/wiki/File:Linear_regression.svg, Sewaqu
Data: $\mathcal{D} = {(x_i, y_i)}_{i=1}^{N}$
Model: $\hat{y} = wx + b$
Loss: $loss = \frac{1}{N}\sum_{i=1}^N(y_i - \hat{y_i})^2$
Neural Network의 출력값(예측값)과 실제값의 차이를 줄이는 것이 궁극적인 목표이다.
Loss를 최소화하는 $w$와 $b$를 찾아야 하므로 back propagation을 통해 $w$와 $b$가 어느 방향으로 갔을 때 Loss가 줄어드는지를 찾는다.
반복적으로 optimization variables를 업데이트 한다.
$\eta$인 Step Size가 너무 크거나 작으면 학습이 제대로 되지 않는다.
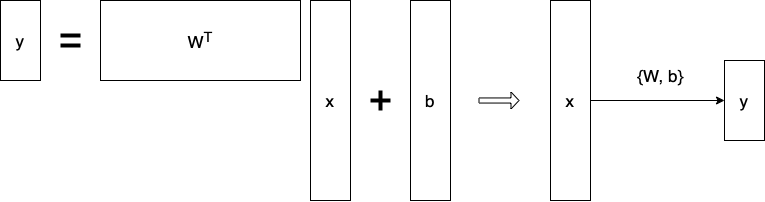
$\mathbf{y} = W^T\mathbf{x} + \mathbf{b}$
1차원 말고도 2차원 이상의 다차원에 관한 데이터에 관해서는 행렬을 이용할 수 있다.
행렬을 곱하는 것은 두 개의 vector space의 변환이라고 이해하는 것이 바람직하다.
Multi-Layer Perceptron(MLP)
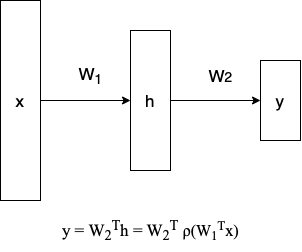
Linear neural network를 여러겹 쌓는 연산은 결국 행렬 2개의 연산에 $x$를 곱한 것과 다름이 없어 여러 번 쌓는 의미가 없다.
표현력을 최대한 극대화하기 위해서는 한 번 선형 결합이 반복되면 $\rho$처럼 이에 관해 여러 가지 Activation Function을 거쳐서 Nonlinear Transformation을 적용한다.
Activation Functions(활성 함수)
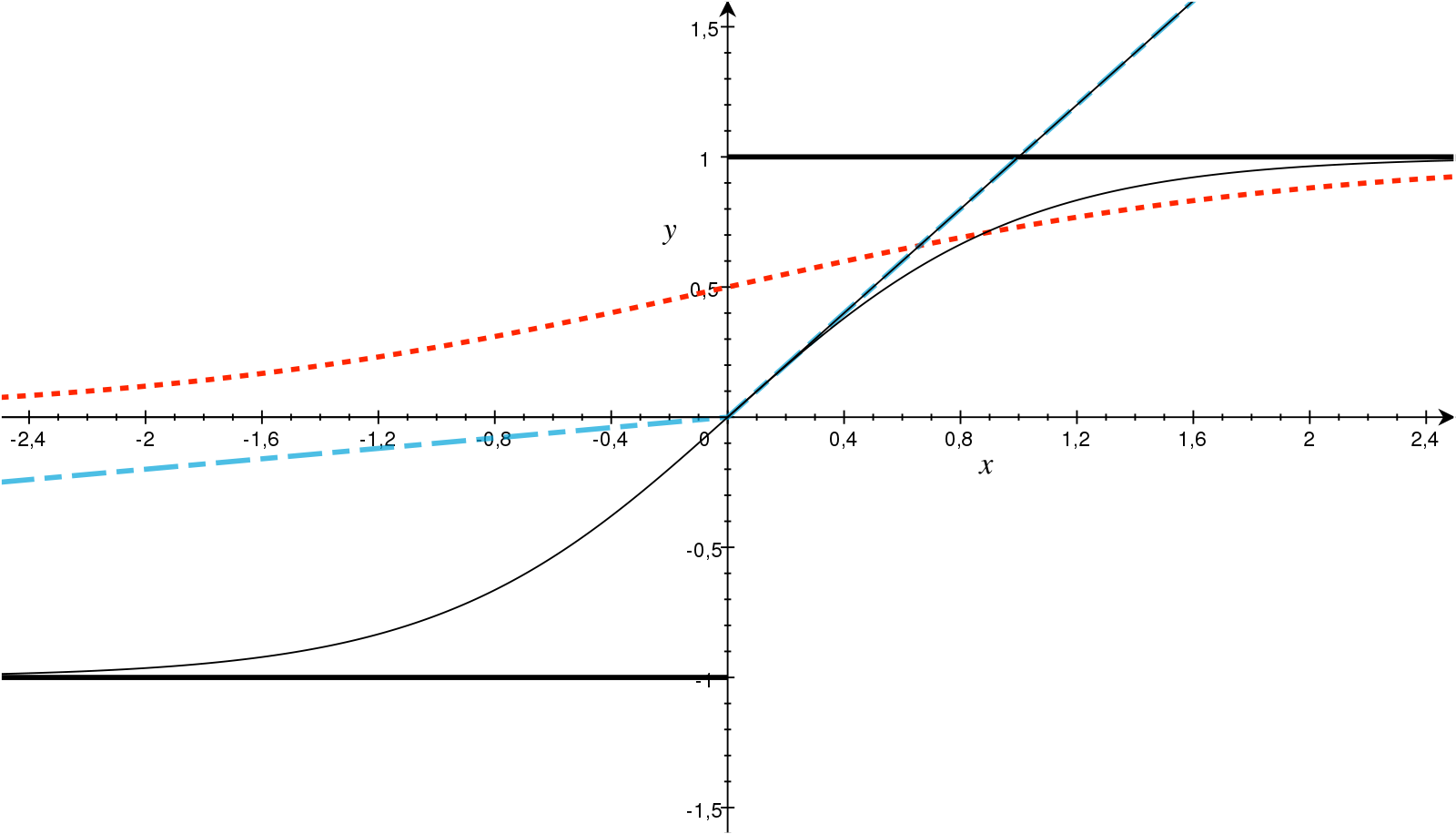
[출처] https://commons.wikimedia.org/wiki/File:ActivationFunctions.svg, Andreas Maier
Neural Network에 비선형성을 부여하는 대표적인 활성함수는 다음과 같다.
- Rectified Linear Unit (ReLU)
- Sigmoid
- Hyperbolic Tangent
Hidden Layer가 하나 있는 Neural Network는 대부분의 continuous하고 measurable한 function을 우리가 원하는 지점까지 근사할 수 있다.
Hidden Layer가 한 개 있는 Neural Network의 표현력은 우리가 표현할 수 있는 대다수의 continuous한 function을 포함한다.
Neural Network의 표현력이 굉장히 크다는 것을 시사한다. 하지만 근사할 수 있는 그 function을 찾는 것은 또 다른 얘기이다.
Loss Function
Loss Function이 어떤 성질을 가지고 있고, 이 function이 왜 우리가 만드는 모델을 학습시키는 데 바람직한지를 생각해 봐야 한다.
Regression Task
Mean Squared Error
Classification Task
Cross Entropy
분류 문제에서 특정 차원 또는 클래스에 해당되는 출력값만 높이겠다는 의미이다.
Probabilistic Task
Maximum Likelihood Estimation
Uncertainty(불확실성) 정보를 같이 찾고 샆을 때 likelihood를 Maximize하기 위해 사용한다.
MLP 생성 코드
class MultiLayerPerceptronClass(nn.Module):
"""
Multilayer Perceptron (MLP) Class
"""
def __init__(self,name='mlp',xdim=784,hdim=256,ydim=10):
super(MultiLayerPerceptronClass,self).__init__()
self.name = name
self.xdim = xdim
self.hdim = hdim
self.ydim = ydim
self.lin_1 = nn.Linear(
self.xdim, self.hdim
)
self.lin_2 = nn.Linear(
self.hdim, self.ydim
)
# 각 파라미터들을 초기화해주는 부분
self.init_param()
def init_param(self):
# 각 linear function의 w, b 초기화
nn.init.kaiming_normal_(self.lin_1.weight)
nn.init.zeros_(self.lin_1.bias)
nn.init.kaiming_normal_(self.lin_2.weight)
nn.init.zeros_(self.lin_2.bias)
def forward(self,x):
net = x
# 선형 연산
net = self.lin_1(net)
# 비선형 연산
net = F.relu(net)
# 비선형 연산
net = self.lin_2(net)
return net
# 모델 생성
M = MultiLayerPerceptronClass(name='mlp',xdim=784,hdim=256,ydim=10).to(device)
# loss는 CE로
loss = nn.CrossEntropyLoss()
# Adam Optimizer, learning rate는 0.001로
optm = optim.Adam(M.parameters(),lr=1e-3)
파라미터를 초기화하는 여러 방법은 torch.nn.init에서 제공하고 있으며, 아래 기술 문서에서 자세한 내용을 확인할 수 있다.
https://pytorch.org/docs/stable/nn.init.html#torch.nn.init.kaiming_normal_
torch.nn.init — PyTorch 1.11.0 documentation
Shortcuts
pytorch.org
Model의 Feed Forward 연산
x_numpy = np.random.rand(2,784)
# gpu로 torch객체를 등록해주는 코드
x_torch = torch.from_numpy(x_numpy).float().to(device)
# y_torch = M(x_torch)와 동작이 같음
y_torch = M.forward(x_torch)
# cpu로 객체를 등록해주는 코드
y_numpy = y_torch.detach().cpu().numpy()
Evaluation
def func_eval(model,data_iter,device):
# no_grad로 실행
with torch.no_grad():
# evaluation 모드로 전환
model.eval()
n_total,n_correct = 0,0
for batch_in,batch_out in data_iter:
y_trgt = batch_out.to(device)
model_pred = model(
batch_in.view(-1, 28*28).to(device)
)
_,y_pred = torch.max(model_pred.data,1)
n_correct += (
y_pred==y_trgt
).sum().item()
n_total += batch_in.size(0)
val_accr = (n_correct/n_total)
# train 모드로 전환
model.train()
return val_accr
Train
print ("Start training.")
M.init_param() # initialize parameters
M.train()
EPOCHS,print_every = 10,1
for epoch in range(EPOCHS):
loss_val_sum = 0
for batch_in,batch_out in train_iter:
# Forward path
y_pred = M.forward(batch_in.view(-1, 28*28).to(device))
loss_out = loss(y_pred,batch_out.to(device))
# Update
optm.zero_grad() # reset gradient
loss_out.backward() # backpropagate
optm.step() # optimizer update
loss_val_sum += loss_out
loss_val_avg = loss_val_sum/len(train_iter)
# Print
if ((epoch%print_every)==0) or (epoch==(EPOCHS-1)):
train_accr = func_eval(M,train_iter,device)
test_accr = func_eval(M,test_iter,device)
print ("epoch:[%d] loss:[%.3f] train_accr:[%.3f] test_accr:[%.3f]."%
(epoch,loss_val_avg,train_accr,test_accr))
print ("Done")
출처
1. 네이버 부스트캠프 AI Tech Stage 1 기초 강의
'AI > AI 기본' 카테고리의 다른 글
| 순차 데이터와 RNN(Recurrent Neural Network) 계열의 모델 (0) | 2022.02.17 |
|---|---|
| 딥 러닝에서의 일반화(Generalization)와 최적화(Optimization) (0) | 2022.02.16 |
| 딥 러닝에서 알아두어야 할 요소와 역사적으로 중요한 모델 (0) | 2022.02.16 |
| PyTorch 딥 러닝 과정에서 자주 발생하는 문제 해결을 위한 팁 (0) | 2022.02.15 |
| PyTorch에서의 하이퍼파라미터(Hyperparameter) 튜닝 (0) | 2022.02.15 |
소중한 공감 감사합니다.